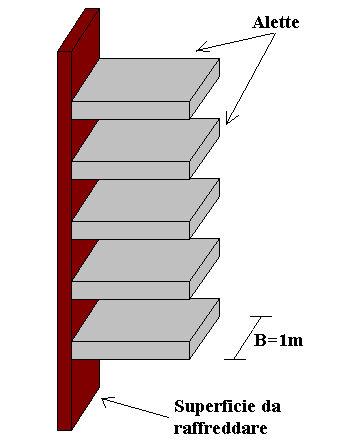
Superfici alettate
In molti casi è necessario aumentare lo scambio termico per evitare il surriscaldamento di particolari componenti, soprattutto nel caso di transistors, chips e altri dispositivi elettronici. Si usano pertanto le superfici alettate, che sono un modo semplice e poco costoso di aumentare la superficie disperdente di un oggetto, ovviando così alla scarsa convezione naturale dell' aria.
Verranno qui viste solo le alette a sezione rettangolare: esse possono in pratica essere viste come una serie di "costole" rettangolari che sporgono da una superficie rettangolare, studiando in tal modo il problema in una sola dimensione (con alette di forma più complessa, invece il problema è di tipo tridimensionale).Esistono comunque alette di varie forme :a spillo, coniche, triangolari.

Figura 1 - superficie alettata
Studio della dispersione
Studiando ora una singola aletta fuori dalla superficie, si vede che essa è descritta da due parametri:
per semplificare, si pone la terza dimensione, cioè la profondità dell' aletta uguale a 1 metro, oppure infinita.
Il funzionamento dell' aletta è il seguente: il calore va per conduzione nel metallo ed è in seguito disperso per convezione dalle due facce superiore e inferiore e, in misura minore, dalla testa. Contro quel che si potrebbe credere , però, l' aumento di scambio termico non è proporzionale alla superficie, perchè la temperatura dell' aletta varia col fluire del calore in essa: un' aletta con grande L sarebbe dunque fredda all' estremità, per cui oltre una certa L non ha senso impiegare materiale per avere solo un piccolo aumento del calore disperso.
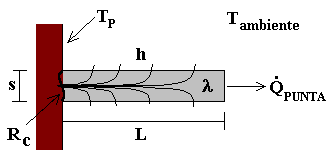
Figura 2 - dispersione del calore in un' aletta
Si deve allora supporre che la resistenza termica R non sia trascurabile lungo la direzione x, ma la si suppone costante su una sezione infinitesima dx (su questo spessore la T è considerata costante).
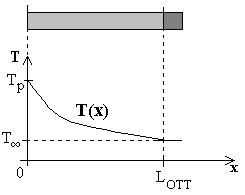
Figura 3 - temperatura dell' aletta in funzione della distanza
Nel caso di alette sottili, cioè L >> s, si fa lo stesso studio degli scambiatori: si studia il tratto dx e si vede quanto calore dQ viene scambiato: si evidenzia allora un flusso di calore che entra ed esce per conduzione a destra e sinistra della sezione dx, e un flusso per convezione dalle facce superiore e inferiore :dQ
![]() Sapendo che la potenza di conduzione è per la legge di Fourier:
Sapendo che la potenza di conduzione è per la legge di Fourier:
![]()
mentre si ha Q2 dallo sviluppo di Taylor di Q1:
![]()
![]() da cui si ottiene:
da cui si ottiene:
Infine, il flusso disperso dalle facce per convezione è :
![]()
Allora:
![]()
L' equazione omogenea ottenuta governa il fenomeno nell' aletta; facendo un cambio di variabile si ha:
![]()
che è l' equazione di D' Alembert (già vista in acustica), le cui soluzioni sono:
![]()
tale condizione, diversamente dall' acustica, qui è sempre verificata per cui non si verificano oscillazioni. Si possono quindi determinare A e B usando le condizioni al contorno per x=0 e x=L: allora si ricorda che a margine dell' aletta (cioè a x=0) c'è una resistenza di contatto (l' aletta in genere non è parte del componente, ma viene attaccata ad esso in seguito). Però il calcolo si complica sulla testa dell' aletta per la convezione: si usa allora, nel caso di alette sottili, una lunghezza dell' aletta di L+s/2 (come se la superficie della testa dell' aletta venisse aperta e attaccata metà alla superficie inferiore e metà alle superiore), che permette di tener conto anche della dispersione della testa.
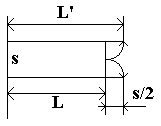
Figura 4 - come ottenere L+s/2
![]() Si possono allora porre le seguenti condizioni al contorno
Si possono allora porre le seguenti condizioni al contorno
![]()
e si ottengono i seguenti valori di A e di B:
![]()
![]() Da cui
Da cui
![]()
Sapendo che
![]()
Si integra allora la potenza su tutta L e si ottiene una risultante finale che è
![]()
Ricordando comunque che il secondo temine del denominatore va a 0 se l' aletta è fusa col corpo e che il termine 2hDT è la potenza che sarebbe scambiata se l' aletta fosse isoterma.
Efficienza termica dell' aletta
![]()
E' il rapporto fra la potenza scambiata e la potenza scambiata se l' aletta fosse isoterma ed è
![]()
Si vede che l' efficienza decresce aumentando L: se L tende a infinito l' efficienza va a 0 e la potenza scambiata tende a un valore massimo non superabile; comunque non sono mai usate alette con efficienza inferiore al 40%
Efficienza dell' alettatura
Quando si attacca un' alettatura a una superficie, se ne studia l' efficienza totale (in genere più alta di quella della singola aletta). La superficie si divide in non alettata Spiana (non ricoperta da alette, con efficienza di scambio uguale a1, si trova alla temperatura della parete e scambia direttamente con la temperatura ambiente) e in alettata Sal (data dalla somma dell' area delle basi delle alette), per cui si hanno le relazioni:
![]()
![]()
![]()
con Ssvil superficie di sviluppo effettivo dell' aletta e Spiana superficie di base: si ha allora che:
![]()
con Sal,tot superficie sviluppata complessiva = superficie piana + superficie sviluppata e eal,tot efficienza dell' alettatura.
I costruttori di superfici alettate forniscono in genere dei diagrammi che mostrano l' efficienza dell' alettatura in funzione di un rapporto dimensionale, per esempio fra la lunghezza e la superficie, o anche di rapporti più complessi (usati per alette non diritte); si tratta dunque di diagrammi sperimentali sulla perdita di efficienza in funzione della geometria.
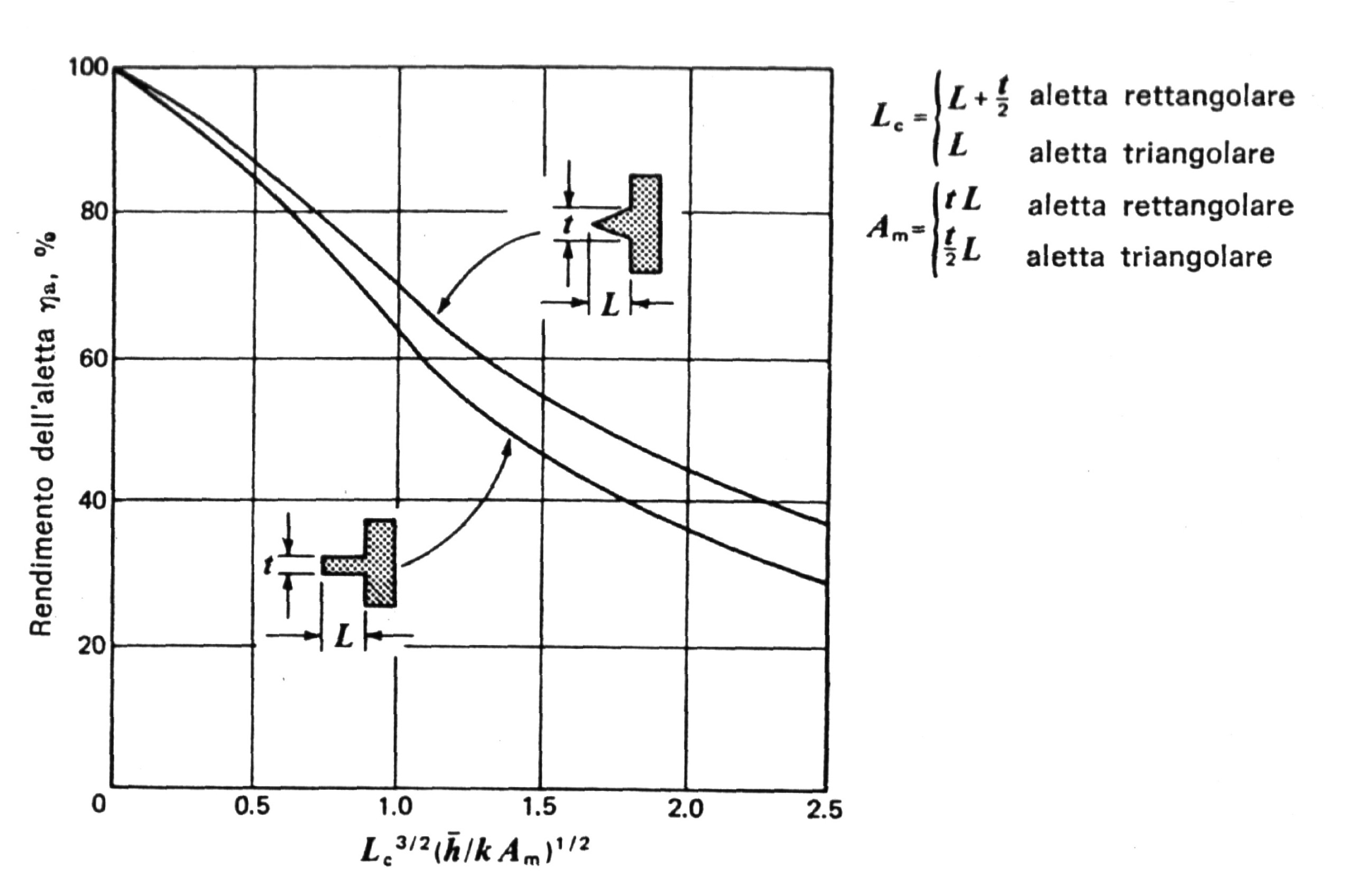
Figura 5 - efficienza di un' aletta rettangolare e di un' aletta triangolare
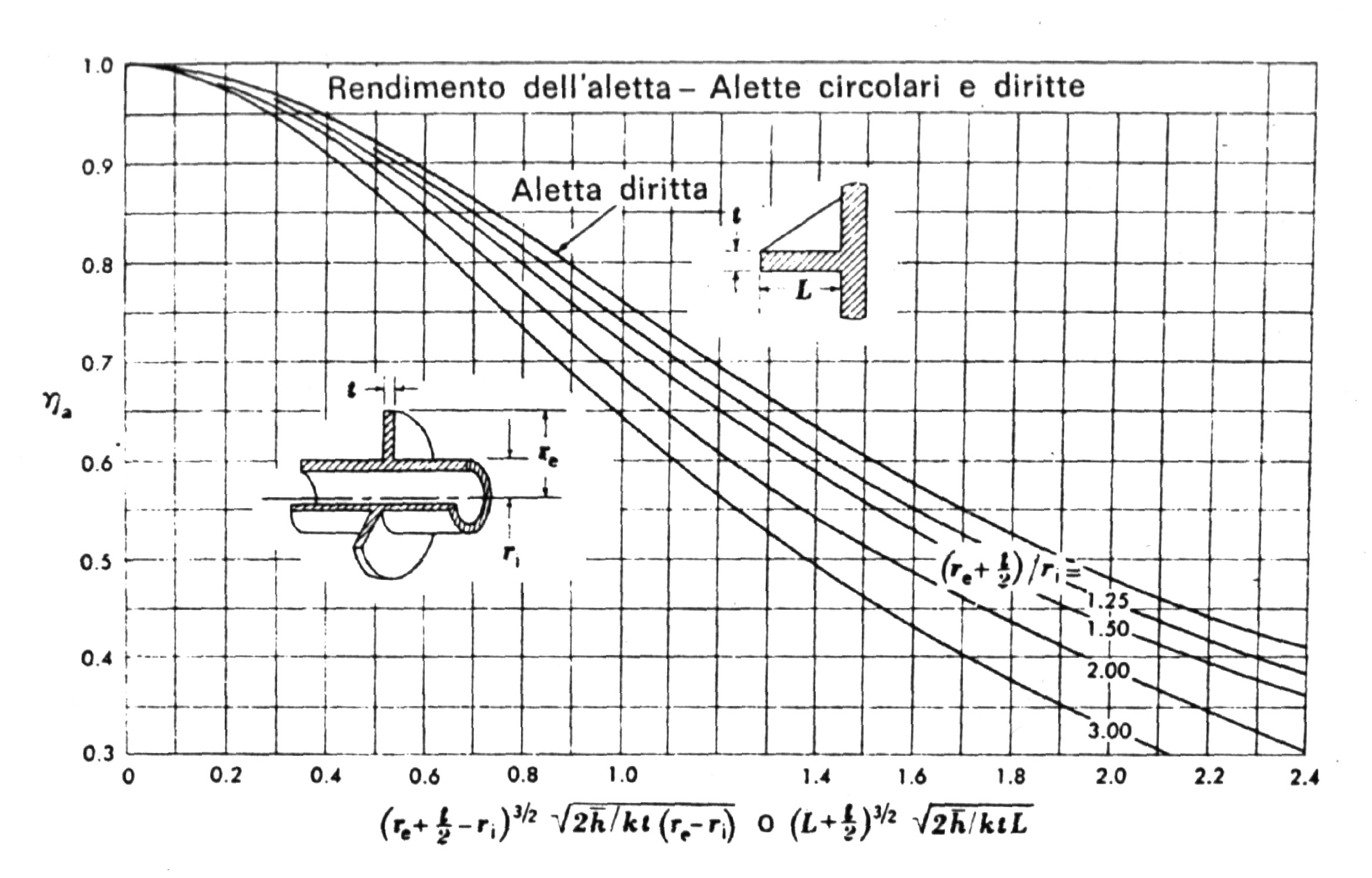
Figura 6 - rendimento di alette circolari e diritte
ESERCIZIO: dispersione per un componente elettronico
Si ha una CPU quadrata di lato 50mm posta in verticale, e se ne vuole sapere la temperatura sia nel caso che non abbia alettatura, sia nel caso che ne venga applicata una. Sia la temperatura ambiente di 20°C e il calore dissipato 20W.
CASO A: nessuna alettatura:
C'è solo scambio termico:
![]()
Serve allora conoscere h, cioè la convezione naturale: si cerca allora il numero di Grashof Gr, la cui espressione è data da
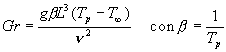
Dove g è la gravita', b il coefficiente di dilatazione termica (inverso della temperatura per i gas), L il lato della superficie quadrata, n la viscosita' cinematica dell' aria. Si ha allora (prendendo come temperatura di primo tentativo 100°C)
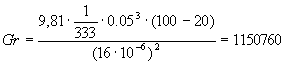
tenendo poi presente che in questo caso il numero di Prandtl Pr è circa 0.71, si ha che il numero di Raleigh Ra è
![]()
cioè molto minore di 109 : ci si trova in situazione di moto laminare, per cui dalle tabelle si può ricavare la formula del numero di Nusselt Nu:
![]()
e dal numero di Nusselt si puo' infine ricavare il coefficiente di convezione h:
![]()
si puo' allora trovare la temperatura della CPU, che è
![]()
Come si vede, è molto alta: non è allora possibile trascurare gli effetti dovuti a irraggiamento, e di conseguenza si usa un coefficiente htot=h+hR da cui si ricava
![]()
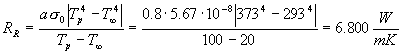
che dà una temperatura finale di
![]()
![]()
che è una temperatura troppo alta per un componente elettronico.
CASO B: Con alettatura:
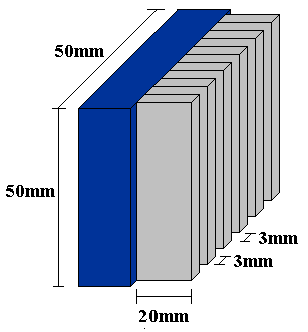
Figura 7 - applicazione dell' alettatura
Si usa un' alettatura commerciale di alluminio, con L=20 mm, alette spesse 3 mm e spaziate 3 mm, che occupano perciò il 50% della superficie della CPU. Si vede che in 50 mm si hanno 8 alette:
S=0.05+0.05=Sal+Spiana
con
![]()
Si pone allora
![]()
![]()
![]() (essendo la superficie totale delle alette)serve quindi l' efficienza dell' aletta, che si può ricavare sia dalle tabelle del costruttore che dalle formule viste nei capitoli precedenti:
(essendo la superficie totale delle alette)serve quindi l' efficienza dell' aletta, che si può ricavare sia dalle tabelle del costruttore che dalle formule viste nei capitoli precedenti:
![]() dal diagramma si ricava allora che il coefficiente eA è 0.93 e si ottiene dunque una temperatura:
dal diagramma si ricava allora che il coefficiente eA è 0.93 e si ottiene dunque una temperatura:
E' accettabile, per la CPU ed è vicino alla temperatura di 100°C con cui si erano fatti i calcoli per l' irradiazione e l' irraggiamento; se invece la temperatura fosse risultata essere più alta, si sarebbe potuto ricorrere ad alette un po' più lunghe (essendo l' efficienza elevata, un ulteriore allungamento delle alette sarebbe ancora conveniente) oppure si potrebbe usare una ventola per migliorare la convezione dell' aria.