Esercizi di scambio termico per irraggiamento

UNIVERSITA’ DEGLI STUDI DI PARMA

Anno accademico 2000-2001

Corso di laurea : ingegneria delle telecomunicazioni

Corso di fisica tecnica

Docente del corso : Angelo Farina

Relazione della lezione di fisica tecnica tenuta il giorno 18/12/2000 alle ore 16 :30-18 :30

Esercizio 1

Questo esercizio studia il caso particolare di due superfici ,due corpi grigi, poste l' una di fronte all' altra, separate da una cavità e poste a temperature differenti T₁ e T₂ .

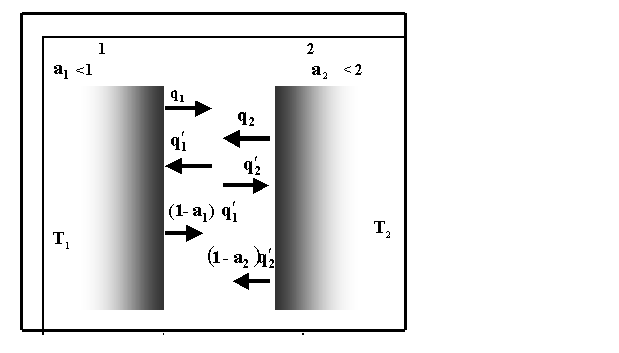
Fig.1 Scambio termico tra due corpi grigi

Di tali superfici sono anche noti i coefficienti di assorbimento a₁ e a₂ (di conseguenza anche quelli di riflessione).

In questa situazione vogliamo trovare il ovvero il potere emissivo

Sappiamo che ciascuna delle due pareti emette una potenza e e che invece su ognuna delle due incide una potenza complessiva che chiameremo per s₁ e per s₂.

Bisogna però anche considerare che sia l'una che l'altra riflettono e che quindi avremo in gioco altre due "pacchetti" energetici cioè la potenza (1-a₁) appunto riflessa da s1 e ovviamente (1-a₂) da s₂.

Da queste informazioni possiamo ricavare un sistema a 2 incognite :

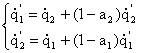(0)

Questo sistema è stato ovviamente ricavato dal bilancio energetico su ogni superficie.

NB: in realtà ,come avviene per lo studio dell' acustica , bisognerebbe considerare questo caso come un transitorio cioè studiare tutti i possibili rimbalzi energetici passo dopo passo.

Però negli studi di scambio del calore tali fenomeni avvengono talmente rapidamente che fare un bilancio finale non comporta l' insorgere di un errore rilevante. Quindi possiamo risolvere questo semplice sistema ottenendo :

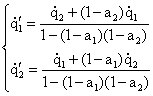(1)

Se conosco le due potenze incidenti possiamo fare il bilancio su ognuna delle due

superfici con la relazione di Prevost e unire il risultato con l' equazione di

Stefan-Boltzmann per ottenere :

(2)

Ricordando ,dalla teoria precedentemente studiata ,che

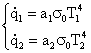(3)

Dove σ₀ è la costante di Boltzmann =5.67 10^-8 combiniamo la (2) con la (3) ottenendo che :

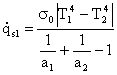(4)

N.B. il valore assoluto permette di considerare anche il caso T₂>T₁

ESEMPIO NUMERICO :

In questo esempio diamo dei dati numerici per renderci conto di cosa succede dimensionalmente

T₁=400K a₁=0.8

T₂=300K a₂=0.6

Sostituiamo cioè nell' equazione trovata precedentemente valori che potremmo trovare in un problema reale otteniamo :

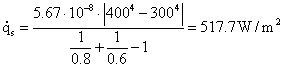(5)

Volendo quindi calcolare la resistenza termica (qui per unità di superficie ) ottengo

(6)

Si può anche trovare il coefficiente di irraggiamento , cioè

Questo risultato è dimensionalmente concorde con i problemi già visti di convezione tanto che , in genere , non si può non considerare la portata di un fenomeno come l' irraggiamento. La trascurabilità di questi risultati cambia poi a seconda dell' ambito in cui si lavora (in acqua per esempio non si considera ).

Esercizio 2

Questo esercizio vuole mostrare sia l' importanza di un fenomeno come l' irraggiamento nella realtà che l' utilità dei calcoli fatti in precedenza per lo studio delle reti elettriche equivalenti. Analizza infatti il caso dello scambio di calore tra due pareti, una di cemento e una di mattoni, entrambe intonacate (fig.2 ). La struttura elettrica equivalente è mostrata nella stessa figura.

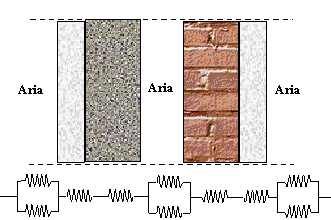
Fig.2 Parete multistrato e rete elettrica equivalente

Sono noti gli spessori di tutti gli strati:

Spessore 1° strato: intonaco 1cm

Spessore 2° strato: cemento 10cm

Spessore 3° strato: aria 5cm

Spessore 4° strato: mattoni 20cm

Spessore 5° strato: intonaco 1cm

Si vuole ricavare la potenza che si disperde attraverso la parete multistrato.

Le conducibilità dei vari materiali sono rese note:

1. λ₂ = l_cemento = 1W/mk

2. λ₃ =l_mattoni = 0.5W/mk

3. λ_1,4 = l_intonaco = 0.2W/mk

E’ noto anche il coefficiente di convezione dell’ aria poiché non bisogna dimenticare che nella cavità si verificano sia irraggiamento che convezione.

h=5W/m²K

Quanto valgono quindi le resistenze?

Sapendo che S=1m² e conoscendo le conducibilità ottengo :

parte raggiante 1/h_r

1° strato S₁/l₁ 2° strato S₂/l₂ 3° strato S₃/l₃ 4° strato S₄/l₄

parte convettiva 1/h

Per calcolare il coefficiente di irraggiamento h_r utilizziamo il coefficiente di assorbimento

a₁=0.6

a₂=0.8

E le temperature T_intonaco1=20°C e T_intonaco2=0°C.

All’ intercapedine si può pensare invece una DT (T_p4-T_p3) di 10 ^oC

Quindi come primo tentativo ipotizziamo T_p3= T_cemento=5°C e T_p4 =T_mattoni=15°C .

Questa ipotesi alla fine risulterà essere assolutamente ragionevole anche se all' inizio le due temperature sono ricavate dalla sola intuizione di chi svolge l' esercizio.

Da questi dati ottengo il calore scambiato per irraggiamento

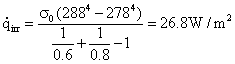(7)

E da esso ricavare h_r tramite l’ equazione = h_rΔT dove ΔT=10°C

Otteniamo così h_r = 2.68W/m²K

Risolviamo con tali informazioni la rete equivalente sapendo che le due resistenze centrali sono in parallelo (vedere figura 2 ) e possono dunque essere sostituite con una resistenza equivalente

(8)

La resistenza totale, essendo somma di resistenze (sempre in figura 2 ) in serie è facilmente calcolabile come

(9)

Siamo in vista del traguardo! Infatti (10)

che rappresenta la potenza che se ne va attraverso la parete multistrato.

FATTORE DI FORMA O DI VISTA

Questo nuovo parametro ci permetterà di studiare lo scambio termico per irraggiamento fra due e più corpi tenendo in considerazione proprietà ,come l' orientazione relativa tra superfici ,che altrimenti rappresenterebbero un problema assai complesso. Per capire di cosa si tratta facciamo un semplice esempio :

se ho due corpi A e B che si scambiano calore accade che parte della potenza emessa dal corpo A ()viene recepita dal corpo B() mentre un' altra parte si perde; questo è dovuto agli effetti della orientazione sulla trasmissione del calore per irraggiamento tra due superfici .

E inoltre abbastanza comune il fenomeno per il quale si recepisce una quantità di calore differente a seconda di come ci si ponga (di fronte o lateralmente) nei confronti di una sorgente.

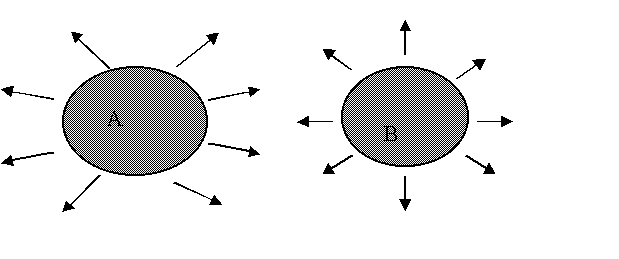
Fig.3 - Scambio termico tra due corpi

Definiamo con fattore di forma ( di vista , di configurazione ,di scambio) il rapporto fra il calore assorbito dal corpo B e il calore totale emesso da A cioè :

(11)

Analogamente

(12)

Che ovviamente rappresenta il rapporto tra il calore assorbito da A e quello totale emesso da B

Questa frazione è quindi basata sull' ipotesi che la radiazione recepita da una superficie è proporzionale all' angolo solido sotto cui viene vista essa stessa dalla sorgente.

Esiste anche un fattore di forma particolare F_AA che è definito come frazione della radiazione della superficie A che colpisce la superficie stessa ; per i corpi convessi più comuni questo varrà ovviamente zero.

Il fattore di vista , nella sua forma più generale, sarà sempre minore uguale ad 1. Il caso visto in precedenza delle due superfici piane parallele evidentemente implicava un fattore di forma uguale ad uno.

La tabella sottostante (tab1) mostra il fattore di forma tra due cilindri coassiali di lunghezza finita al variare delle loro dimensioni mentre quella successiva (tab 2) indica il fattore di vista del secondo cilindro su se stesso . Questi dati ci serviranno nello studio di particolari problemi in seguito.

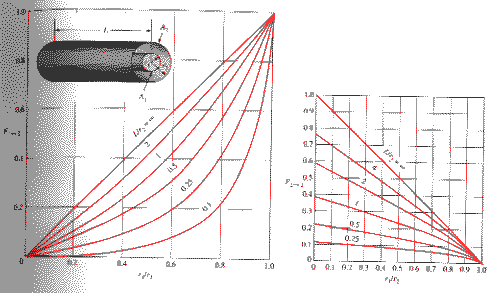
Tab. 1 Fattore di forma di 2 cilindri concentrici.

CASI PARTICOLARI

1) uno dei due corpi è caratterizzato da una superficie Sa piana sterminata mentre l' altro presenta una superficie sferica Sb<<Sa (fig.4)

Fig.4 -Scambio termico tra due corpi di dimensioni non confrontabili

(13)

Valutando invece F_BA si può notare che vale 0.5 poiché metà della potenza dalla sfera (quella emessa dall' emisfero che non si affaccia su S_A) si disperde.

2) Superficie chiusa convessa costituita da due o più parti indipendenti ( in figura 5

è mostrato il caso di tre parti indipendenti)

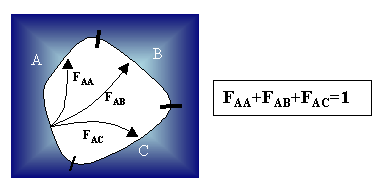
Fig.5 -Corpo concavo formato da tre superfici diverse

Come si può facilmente vedere in figura ogni parte cede energia a se stessa e alle altre, tant' è che svolgendo un semplice bilancio si ottiene che :

(14)

Dividendo quest' espressione per Qa si ottiene

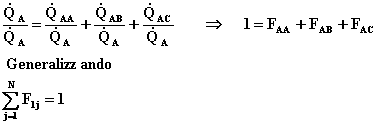(15)

La potenza è cioè equilibrata.

Tale relazione vale quindi per qualsiasi numero N di superfici e non è altro che la formulazione matematica della regola della somma :

la somma dei fattori di vista della superficie i di una cavità verso tutte le superfici della cavità ,essa stessa inclusa, è uguale ad uno.

3) un corpo ha superficie Sa concava contenete un corpo B convesso

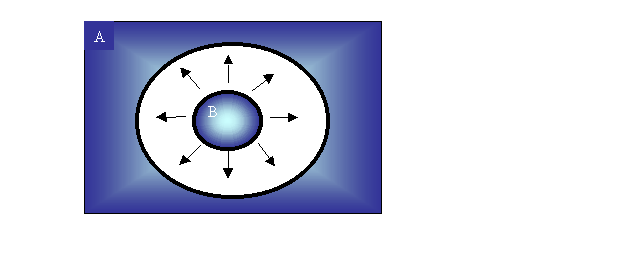Fig.6 -Scambio termico tra un corpo concavo contenente uno convesso

F_BA vale ovviamente 1 poiché tutte le radiazioni emesse da B cadono su A, mentre F_AB non è 1 perché una frazione dell' energia emessa da A si chiude su A stessa, essendo S_b piuttosto ridotta, quindi F_AB<<1

Studiamo meglio questa situazione:

chiamiamo e le potenze emesse da ciascuna superficie, mentre e quelle incidenti.

Possiamo utilizzare gli stessi concetti utilizzati nel primo esercizio, e indichiamo con e le potenze scambiate rispettivamente da A e da B. Otteniamo così un sistema di due equazioni in due incognite che, risolto, ci permette di ricavare

Pertanto sarà:

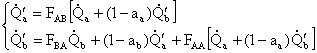(16)

risolvendo il sistema per sostituzione, otteniamo:

; (17)

ricordando che è F_BA=1 e F_AA=1-F_AB e utilizzando la relazione di Prevost (per la potenza scambiata complessiva) si ha:

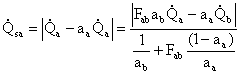. (18)

Dato che si ha poi:

, , (19)

la (18) equivale alla relazione:

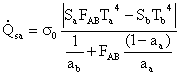, (20.a)

che nel caso di superfici completamente affacciate (F_AB=1 e S_a= S_b), considerando anziché mi permette di ottenere 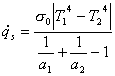(20.b)

che è , ovviamente lo stesso risultato del primo esercizio

La (20) consente inoltre di determinare rapidamente il valore di F_AB; infatti se T_a=T_b, deve essere anche Q_s=0, per cui dovendosi annullare il numeratore della (20) deve essere:

. (21)

E’ una relazione che vale solo se il corpo B è convesso (altrimenti emetterebbe in parte su di sé e i nostri calcoli precedenti non sarebbero più validi) e se entrambe le superfici sono isoterme.

Consideriamo un caso particolare: S_a/S_b molto grande, cioè F_AB<<1. Nella (20) posso trascurare il 2° termine al denominatore; ricordando che possiamo scrivere S_b=F_ABS_a si ottiene:

. (22)

Si osserva quindi che per un corpo dentro un ambiente grande (situazione frequente nei nostri problemi), entrambi grigi, si ottiene una relazione come se esso fosse contenuto in un corpo nero.

Esercizio 3

Consideriamo un forno rotante per la cottura del cemento: si tratta essenzialmente di un cilindro rotante attorno al suo asse. Lo scambio termico sulle facce è trascurabile poiché la dispersione del calore avviene solo lateralmente. Si chiede di determinare la potenza dispersa dal forno prima che si operi qualche modifica per limitarla.

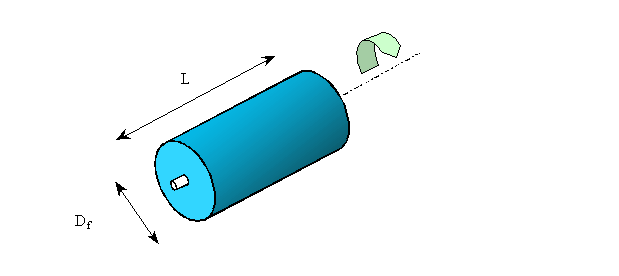
Fig.7 -Forno rotante per la cottura del cemento

Dati del problema :

D_f=1.5m

L=5m

T_p=523K

T_∞=300K

a=0.8

La soluzione è immediata, infatti

= (23)

con S=πD_fL

Questa potenza risulta essere eccessiva; per ridurla si installa un secondo tubo formato da un foglio di lamiera zincata (non rotante) il cui diametro D_s è 2.25m e il cui coefficiente di assorbimento a_s è 0.4

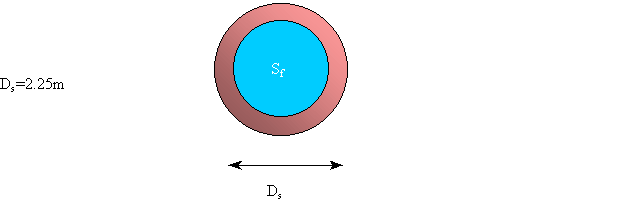
Fig.8 -Sezione del forno schermato

Fig.9 -Rete elettrica equivalente

Chiamando le due superfici di forno e lamiera S_f e S_s possiamo risolvere rapidamente il problema ,ovviamente la nostra nuova incognita sarà la potenza .

Teoricamente lo schermo stesso dovrebbe avere una resistenza termica conduttiva che però (come si vede in figura 9 ) è trascurabile in questo caso.

Di conseguenza la potenza scambiata sarà

(24)

Questa situazione implica l' uso della forma complessa dell' equazione trovata in precedenza, in quanto le due superfici sono confrontabili tra loro. Uguagliando quest' espressione con la prima calcolata si ottiene una "semplice" equazione con incognita T_S

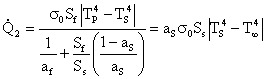(25)

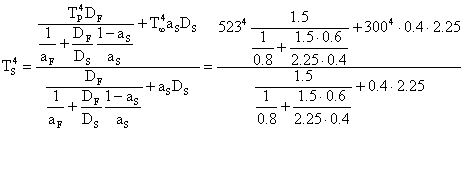(26)

T_s = 437K che permette di trovare con una delle due equazioni trovate ,in questo caso la (25),

(27)

Si è quindi ridotta di più di un terzo la potenza scambiata senza introdurre alcun isolante.

Esercizio 4

Completiamo la trattazione dell' esercizio sulla convezione del 12-12-00 (per maggiore precisione vedere la tesina di Sordi Francesco ) in cui si cercava di impedire fenomeni di arrugginimento da parte di un tubo attraverso uno strato isolante .

Si era ipotizzato un diametro dell' isolante posto intorno al tubo preso in considerazione pari a 20mm. Conoscendo il coefficiente di assorbimento, la conducibilità termica, il coefficiente di convezione interno ed esterno, ci si domanda se i risultati precedentemente ottenuti sono ancora validi alla luce della conoscenza dei fenomeni di irraggiamento.

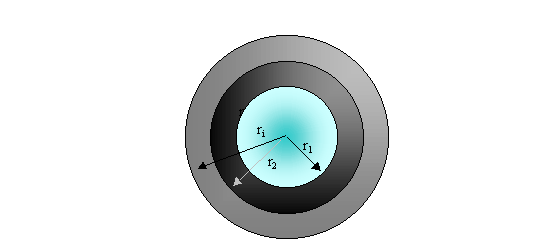
Fig.10- Sezione del tubo

Dati

Usando la formula semplificata per l’irraggiamento (non lineare):

(28)

Dalla definizione di coefficiente di irraggiamento so che :

(29)

Quindi sostituendo numericamente si ha:

(30)

Nella nuova rete elettrica equivalente bisogna introdurre una resistenza in parallelo rispetto a quella convettiva; questo non comporta nessun cambiamento nella risoluzione del problema, se non dal punto di vista numerico. Si trova infatti che la resistenza totale è

R_tot = 0.6466+0.7879 = 1.434Km/W

A questo punto siamo in grado di calcolare la potenza totale scambiata

(31)

Per trovare infine :

(32)

Quindi il raggio dell’isolante determinato nell’esercizio precedente è ancora valido, essendo la nuova temperatura di parete ancora maggiore di 10°C.