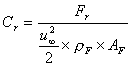MOTO ESTERNO
Il termine "moto esterno" indica quella parte della fluidodinamica che studia il moto dei fluidi intorno ai corpi, o meglio, studia le forze che i corpi ricevono dai fluidi in movimento (o viceversa se sono i corpi stessi a muoversi nei fluidi).
A tale scopo il moto esterno si occupa di tutti quei casi in cui il fluido viene a contatto con la superficie esterna di un oggetto ed è equivalente ai fini fisici che il corpo sia fermo ed il fluido in movimento o che il fluido sia fermo ed il corpo in movimento o, ancora, che si muovano entrambi: studia, in pratica, il moto relativo tra fluido e corpo di contatto.
Il moto
relativo di un fluido rispetto ad un corpo, infatti, provoca su questi sforzi (forze, cioè, per unità di
superficie) che possono essere di due nature, normale e tangenziale.
Gli sforzi
normali sono dovuti alla pressione che il fluido esercita sulla superfice di
contatto del corpo in esso immerso e possono dar luogo a delle forze portanti
(si veda l'ala di un aereo).
Le
interazioni, invece, tra le particelle del fluido a diretto contatto con la
superficie del corpo, che sono ferme rispetto ad esso per l'ipotesi di
aderenza, e quelle vicine, che conservano la velocità iniziale, provocano una
decellerazione del fluido che implica, secondo Newton, uno sforzo tangenziale.
Lastrina Piana
Consideriamo
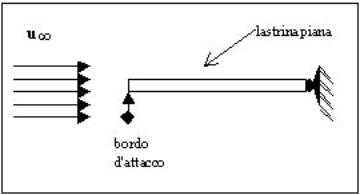
l'esempio semplice di una lastrina piana,
di spessore irrilevante e lunghezza infinita, immersa in un fluido dotato di
una certa viscositA' ![]() .Tale fluido scorre con un profilo di velocità piatto,
diretto parallelamente alle superfici della piastrina, con velocità u
.Tale fluido scorre con un profilo di velocità piatto,
diretto parallelamente alle superfici della piastrina, con velocità u![]() .
.
Situazione ritratta in figura 1.
Fig.1-Lastrina piana investita da un flusso.
Supponendo che, ad una distanza sufficientemente grande, in proporzione alle dimensione dell'ostacolo, il fluido rimanga imperturbato dalla presenza del corpo stesso, restringiamo il nostro campo d’osservazione alle immediate vicinanze della superficie di contatto. Inoltre, grazie all'evidente proprietà di simmetria delle facce della lastrina, possiamo esaminare il solo sistema fluido - superficie superiore, ritenendo speculare quello che avviene sull'altra superficie.
Per l'ipotesi di aderenza,
secondo la quale in tutti i fluidi le particelle a diretto contatto con i
confini solidi non scorrono rispetto al confine stesso, nelle immediate
vicinanze della parete superiore della piastrina il fluido subisce una rapida
decelerazione passando dalla velocità u![]() , velocità del fluido lontano dal corpo, ad una
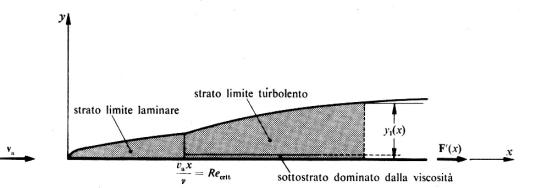
velocità nulla. La porzione di fluido, all'interno della quale le particelle
subiscono questa decelerazione, prende il nome di Strato Limite ed è definito come il luogo dei punti in cui le
particelle hanno una velocità
, velocità del fluido lontano dal corpo, ad una
velocità nulla. La porzione di fluido, all'interno della quale le particelle
subiscono questa decelerazione, prende il nome di Strato Limite ed è definito come il luogo dei punti in cui le
particelle hanno una velocità
![]() (1)
(1)
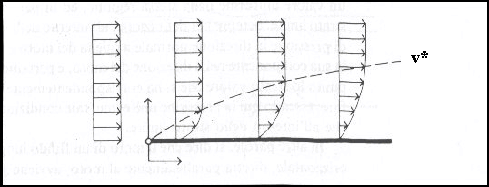
fig.2-Strato limite.
Filo Cilindrico investito da un fluido
Caso Fluido ideale
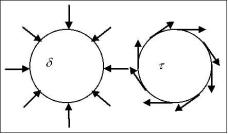
fig.5- Sezione frontale del cilindro con
gli
sforzi tangenziali (![]() ) e normali (
) e normali (![]() ).
).
Avendo
considerato l'aria un fluido ideale gli sforzi tangenziali saranno tutti nulli
e dall'equazione di continuità applicata nelle sezioni 1 e 2 (figura 6) si
ricava che la velocità di fuga del fluido dal corpo è maggiore di quella di
arrivo
![]() (5)
(5)
Molto esternamente, invece, ad una distanza di 10, 15 ,al massimo 20 diametri D dal corpo sono presenti zone in cui gli effetti di perturbazione generati a causa della presenza del corpo stesso risultano praticamente nulli e il fluido continua nel suo moto ignorando la presenza del cilindro.
Nella zona ristretta intorno al solido in cui sono apprezzabili tali effetti il profilo di velocità dell’aria non è più piatto ma risulta essere del tipo mostrato in figura 6.
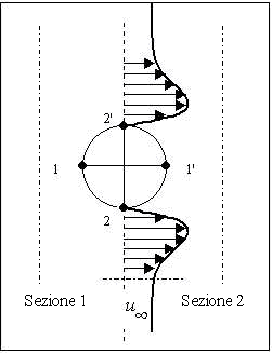
Fig.6 profilo di velocità
Scrivendo l'equazione di Bernulli ,che è applicabile anche in presenza di fluidi ideali otteniamo:
![]() (6)
(6)
questo perché le perdite di carico R sono nulle, avendo considerato l'aria un fluido ideale, la variazione di energia potenziale è trascurabile e non c'è nessuna produzione di lavoro l.
![]()
Essendo, per la (5), u2
maggiore di u1 si ha che
![]() (7)
(7)
dove
p![]() è la pressione dell'aria lontano dal cilindro.
è la pressione dell'aria lontano dal cilindro.
La pressione nei punti 1 e 1', di figura 6, detti punti di ristagno, in quanto la velocità li è nulla, sarà
![]() (8)
(8)
dove pr indica la pressione di ristagno.
Nei punti 2 e 2' si ottiene, dalla (6), un valore della pressione pari a
![]() (9)
(9)
e dalla (8) e dalla (9) si deduce che pr è maggiore sia di p2 sia di p1, e che p2 è minore della pressione atmosferica.
Ora, se fissiamo un sistema di riferimento angolare tale che
![]() punto
1
punto
1
![]() punto 1'
punto 1'
si può
ricavare l'andamento della pressione sulla superficie del cilindro.
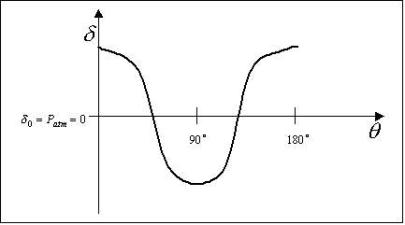
Fig.7-Andamento della pressione sulla superficie del cilindro.
La forza normale dovuta a questa pressione sarà
![]() (10)
(10)
essendo l'elemento infinitesimo
![]() (11)
(11)
dove,
rispettivamente, R è il raggio della
circonferenza base e L la lunghezza
del cilindro, ed essendo, inoltre, la pressione ![]() una funzione
dell'angolo
una funzione
dell'angolo ![]() e la componente
ortogonale del vettore forza la sua proiezione tramite il coseno, si ricava
e la componente
ortogonale del vettore forza la sua proiezione tramite il coseno, si ricava
![]() (12)
(12)
Sostituendo
nella (11), integrando da ![]() a
a ![]() e moltiplicando per
due giacché quanto detto sinora vale in modo del tutto analogo per la parte di
cilindro compresa tra i
e moltiplicando per
due giacché quanto detto sinora vale in modo del tutto analogo per la parte di
cilindro compresa tra i ![]() e
e ![]() si ottiene
si ottiene
![]() (13)
(13)
Il risultato è che gli sforzi normali si equilibrano perfettamente, la forza risultante F è nulla e il cilindro resta fermo nel fluido: paradossale, in quanto, la forza F non è, nella realtà, nulla.
Questa conclusione, cui siamo giunti, servendoci di un fluido ideale, è conosciuta come il Paradosso di D'Alambert che viene così enunciato:
Se il fluido è ideale esso porta ad una forza trasversale nulla.
Il corpo, cioè, non viene né posto in rotazione né quantomeno trascinato dal fluido perché sia la risultante degli sforzi normali che quella degli sforzi tangenziali sono nulle.
Caso Fluido Reale
Verificato
che il fluido ideale non esiste, riconsideriamo l'esempio precedente supponendo
l'aria dotata di una certa viscosità ![]() .
.
Grazie a questa
nuova ipotesi, tra le particelle del fluido e la superficie del cilindro si
genera attrito viscoso che provoca la perdita, per scambio termico, di parte
dell’energia cinetica del fluido; ne consegue che l’aria che attraversa la
sezione 1 ha più energia di quella che attraversa la sezione 2. La conclusione
è che gli sforzi normali, che prima erano perfettamente equilibrati, tendono,
ora, a diminuire in modulo procedendo da ![]() a
a ![]() in senso orario, e
l’andamento della pressione non sarà più come quello di figura 7 ma il
seguente.
in senso orario, e
l’andamento della pressione non sarà più come quello di figura 7 ma il
seguente.
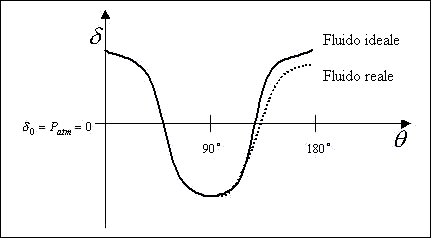
Fig.8-Confronto tra la pressione esercitata sulla superficie
del cilindro dal fluido reale ed ideale.
Questo scostamento, se pur piccolo, provoca uno sbilanciamento degli sforzi normali, i quali non essendo più equilibrati, non danno luogo ad una forza risultante nulla, bensì ad una forza F, che seppur poco apprezzabile perché piccola è la differenza tra la curva reale ed ideale, tende a trascinare l’oggetto.
Per quanto riguarda, invece, gli sforzi
tangenziali, ossia la tensione esercitata tangenzialmente alla superficie del
cilindro, dovuta all’attrito viscoso dell’aria, il cui valore è dato ancora
dalla (3), possiamo ricavarne l’andamento fissando il sistema di riferimento
angolare usato in precedenza.In base ciò si ottiene il seguente grafico.
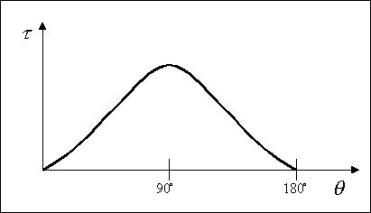
Fig.9 tensione tangenziale lungo la superficie del cilindro.
Dalla tensione tangenziale possiamo ricavare la forza
di trascinamento Ft
![]() (14)
(14)
La Forza risultante delle tensioni tangenziali e
normali è un forza F applicata nel
baricentro del corpo e con direzione e verso rivolto verso ![]() .
.
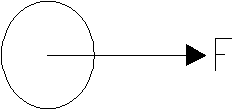
Fig.10-Forza risultante.
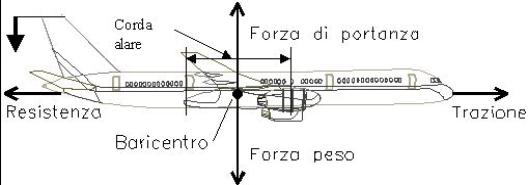
Ali di aereo
Le ali di un
aereo sono gli oggetti che per antonomasia vengono associati allo studio del
moto esterno dei fluidi.
Esse sono costruite per sfruttare al meglio la forza di portanza in modo da far sollevare l’aereo usando la più bassa forza di trazione con un notevole guadagno in termini di rendimento del sistema.
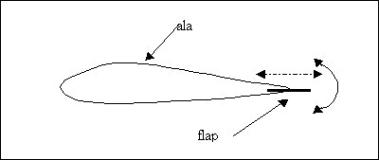
Il profilo di un’ala è quello mostrato nella figura seguente.
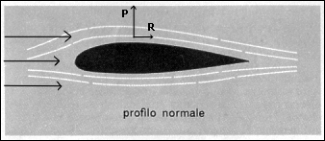
Fig.11-Profilo alare
con flusso d’aria.
Esistono, inoltre, dei diagrammi che rappresentano l’andamento della forza di portanza e di resistenza in funzione del profilo alare (dell’angolo di regolazione dei flaps), della velocità e della densità dell’aria (figura 14).
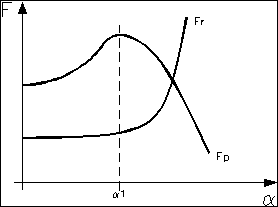
Fig.14- Forza di portanza e forza resistente (aereo).
Si nota che la forza portante risulta maggiore della resistente in un primo tratto; questo è il tratto in cui deve lavorare l’aereo per un rendimento ottimale. L’angolo a1 è detto angolo di stallo.
Per gli aerei il rapporto Fp/Fr è dell’ordine di 4¸5 ma può arrivare a 12 per gli alianti.
Teoria dei Modelli
Fin’ora
abbiamo studiato un caso di problema relativamente facile; ma nonostante ciò
non siamo riusciti a trovare espressioni analitiche semplici per le forze: nel caso reale risulta molto complesso
calcolare analiticamente il valore ![]() e t(q). Per i casi più complessi, ovvero per casi in cui
i solidi non siano delle figure geometriche elementari, è praticamente
impossibile valutare numericamente le grandezze di cui sopra. Nonostante
l’impiego di computer e algoritmi di calcolo sempre più potenti e sofisticati,
la complessità intrinseca del problema è tale da non permettere uno studio
preciso. Per questi motivi, la fluidodinamica esterna viene studiata
principalmente per via sperimentale,
cioè con le cosiddette gallerie del vento
(si veda “Galleria del vento”).
e t(q). Per i casi più complessi, ovvero per casi in cui
i solidi non siano delle figure geometriche elementari, è praticamente
impossibile valutare numericamente le grandezze di cui sopra. Nonostante
l’impiego di computer e algoritmi di calcolo sempre più potenti e sofisticati,
la complessità intrinseca del problema è tale da non permettere uno studio
preciso. Per questi motivi, la fluidodinamica esterna viene studiata
principalmente per via sperimentale,
cioè con le cosiddette gallerie del vento
(si veda “Galleria del vento”).
Lo studio dei sistemi complessi (per esempio ali di aerei, automobili, radiatori, ecc.) richiederebbe, specialmente per oggetti di grandi dimensioni, gallerie del vento molto grosse e quindi molto costose. A questo inconveniente pone rimedio la teoria dei modelli che, come dice la parola stessa, fa uso di modelli in scala del sistema da studiare. Secondo la teoria dei modelli, infatti, è possibile studiare la fluidodinamica esterna di un sistema con lunghezza caratteristica L usando un modello in scala del sistema stesso con lunghezza caratteristica L’<<L, i risultati così ottenuti possono essere riportati sul modello originale tramite numeri puri.
La grandezza
caratteristica di un sistema è la dimensione di una particolare zona presa
come riferimento per tutte le altre e scalando questa viene scalato l’intero
sistema. Nella studio fluidodinamica esterna la grandezza presa come
riferimento è l’Aria Frontale, cioè la superficie della proiezione
dell’oggetto in esame lungo ![]() (per esempio l’Aria
Frontale del sistema aria-filo cilindrico, discusso in precedenza, era il
diametro del cilindro stesso).
(per esempio l’Aria
Frontale del sistema aria-filo cilindrico, discusso in precedenza, era il
diametro del cilindro stesso).
La figura successiva mostra un esempio di aria frontale per un sistema costituito da una automobile immersa in un fluido.
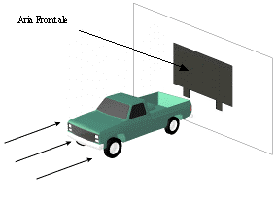
Fig.15-Esempio
di ari frontale.
Come visto nelle precedenti lezioni, il numero di Reynolds si calcola con l’usuale formula
![]() (15)
(15)
dove
u velocità del fluido;
D grandezza caratteristica;
![]() viscosità
cinematica fluido
viscosità
cinematica fluido
Con la teoria dei modelli, invece, eseguiamo prove di laboratorio su un modello in scala con grandezza caratteristica D’<< D trovando un valore del numero di Reynolds (Re’) che dovrà essere uguale al numero di Reynolds trovato in precedenza sul modello reale (Re). Cioè:
![]() (16)
(16)
In questo caso si nota che, essendo la viscosità cinematica costante (se si suppone uguale la temperatura e lo stesso fluido), affinché i due numeri di Reynolds (numeri puri) rimangano uguali occorre eseguire prove con u’ >> u.
Analogamente al coefficiente di resistenza Cx, che determina la forza di resistenza (di cui tra breve parleremo) che si oppone al moto relativo fluido-oggetto, è possibile determinare il coefficiente di portanza Cp, che determina la forza di portanza, cioè quella forza che spinge verso l’alto il modello (per esempio le ali).
Forza di Resistenza-Forza di Portanza
La forza di resistenza Fr, come abbiamo detto, è la forza che si oppone al moto relativo fluido – corpo, essa tende a trascinare il corpo lungo una direzione.
La sua espressione analitica è
![]() (22)
(22)
u velocità
fluido
AF aria
frontale
![]() densità
fluido
densità
fluido
La forza di portanza Fp è la forza responsabile della spinta verso l’alto (o verso il basso) di un oggetto. Per esempio le ali di un aereo sono geometricamente studia per ottenere una forza di portanza più elevata possibile, mentre la geometria delle auto da corsa è tale da ottenere una forza di portanza rivolta tutta verso il basso in modo da rendere più stabile possibile la vettura.
La sua espressione analitica è
![]() (23)
(23)
La somma vettoriale della (20) e della (21) dà la forza di
trascinamento totale.
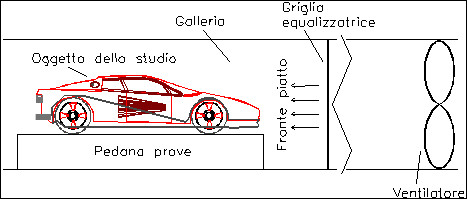
Galleria del Vento
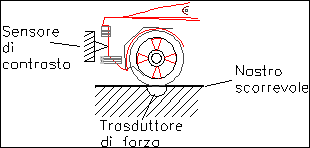
Dalla figura si vede che sulla pedana sono montati dei trasduttori di forza usati per la misura dei carichi aerodinamici scaricati sul terreno e dei sensori di contrasto per misurare la spinta posteriore (oltre che per mantenere fermo il modello).
Inoltre si pongono sulla superficie dell’oggetto in questione diverse decine di piccole cannucce per misurare la pressione nei vari punti e ciò equivale ad avere tubi di Pivot che misurano la velocità dell’aria.