Coronella Pierre 111642 13/11/2000 14:30-16:30 Acustica ed elettroacustica:Generalità e Definizioni
ACUSTICA ED ELETTROACUSTICA
Generalità
L'acustica è una scienza nata quando ancora non esistevano i sistemi di gestione elettrica del suono e ha avuto un impulso incredibile nell'ultimo decennio , a partire dal 1991 , grazie a due fattori fondamentali: il primo è lo sviluppo delle tecnologie a lei connesse che hanno permesso mezzi più affidabili , mentre il secondo è la teoria dell'elaborazione numerica del segnale. Quest'ultima, di riflesso , si è sviluppata fortemente grazie allo studio dell'acustica, poiché è possibile avere un riscontro semplice e veloce dell'elaborazione tramite il nostro proprio udito. Dietro lo studio dei segnali acustici c'è una teoria formale molto pesante ma , per controparte, abbiamo un buon passaggio dal modello alla realtà.
L'acustica è la scienza che studia il suono , un fenomeno meccanico che si sviluppa in un mezzo ( gas, liquidi e solidi ) e il cui studio ha alcuni stadi significativi , ognuno dei quali con particolari accorgimenti.
Innanzitutto avremo lo studio della propagazione del segnale nel mezzo ( principalmente l'aria ), poi dopo il passaggio in un trasduttore ( ottenendone la traduzione ) avremo la relativa gestione di una grandezza elettrica. Il segnale elettrico passerà per un convertitore dove verrà convertito in numeri ed infine elaborato da un algoritmo. L'elaborazione ha innumerevoli funzioni , ad esempio modificare alcuni parametri quali l'ampiezza, la frequenza e l'affidabilità.( fig.1 ).
![]()
Il disegno mostra il diagramma a blocchi di un sistema digitale , ho una catena che percorsa in un senso mi darà dei numeri mentre nell'altro mi darà un segnale acustico. Questa "catena" non deve essere obbligatoriamente completa ma , se realizzata solo con i primi due stadi ( mezzo e trasduttore ) darà luogo ad un sistema analogico e di un sistema acustico se ridotta al solo primo stadio, cioè se il segnale sonoro viene modificato meccanicamente. La scelta del sistema più appropiato sarà determinata in prima analisi dalla tolleranza ai disturbi del sistema e successivamente dal costo. Incominciamo a studiare questi sistemi partendo con la definizione di suono.
Suono
Il suono è un fenomeno di trasporto energetico ( quindi dove si ha un movimento di energia meccanica da un punto ad un altro ) ma non di materia, e in generale diremo che si tratta di energia acustica, sarà così possibile parlare di potenza del segnale, di rendimento, ecc.
Per la propagazione di questa energia sarà necessario un mezzo, che dovrà essere elastico e massivo ( cioè dotati di massa ed elasticità in distribuiti con continuità ). Un esempio esemplificativo di queste due ipotesi è l'esperimento della sveglia sotto la campana una campana di vetro.( fig. 2 )

Fig. 2 - Sveglia
Mentre la sveglia è udibile all'interno della campana nella prima fase dell'esperimento, nella seconda, in cui viene tolta l'aria all'interno di questa ( viene cioè tolto il mezzo che prima era l'aria ), la sveglia non sarà più udibile. Precisiamo che questa non è una trasmissione di onde elettromagnetiche che non richiedono un mezzo ( una teoria dice che sono esse stesse il mezzo, essendo fasci di onde di particelle ). Il mezzo può allora essere idealmente rappresentato come un susseguirsi di masse infinitesime collegate da delle molle. (fig. 3 ).
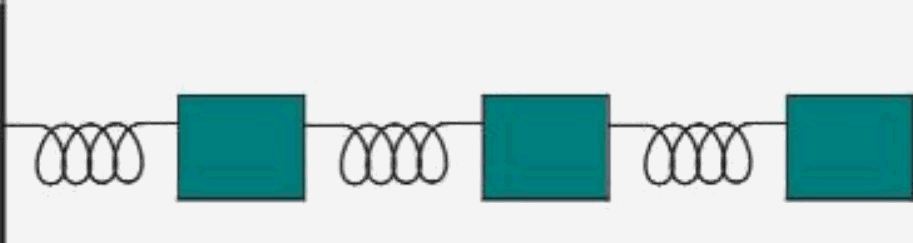
Fig. 3 Mezzo elastico e massivo
Spostando una molla dalla sua posizione di quiete questa incomincia ad oscillare andando avanti e indietro intorno alla sua posizione di equilibrio, cosi facendo carica e scarica le molle a lei adiacenti e quindi il moto della prima massa si trasmette lungo il mezzo. Visto che l'oscillazione intorno al punto di equilibrio potrà avvenire lungo le due dimensioni, potremo distinguere tra due specie: le onde longitudinali in cui il moto delle particelle intorno ad una posizione di equilibrio avviene parallelamente alla direzione dell’onda e le onde trasversali in cui il moto delle particelle è perpendicolare alla stessa. Un esempio della prima può essere un pistone che comprime dell'aria ( fig. 5 ), mentre un esempio della seconda può essere il movimento delle onde del mare ( fig. 4 ).
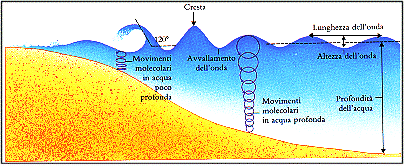
Fig.4 Esempio di onda marina trasversale
Attenzione, però: non solamente le onde sonore trasmettono il suono! Se per esempio considero il caso in cui una persona parla in una stanza, sappiamo che la sua voce potrà essere udita ( se il locale non è eccessivamente insonorizzato ) anche in una stanza adiacente; in questo caso però le onde sonore si propagano nelle infrastrutture sotto forma di altre onde di tipo trasversale ( di taglio, o di riflessione, ad esempio ), le quali poi irradiano onde sonore nell'ambiente ricevente.
Velocità del suono
Chiaramente il fenomeno si sviluppa in un certo tempo, per cui esiste una velocità di propagazione, che chiameremo c. Nei mezzi non dispersivi vedremo che questa velocità sarà la stessa per tutti i tipi di suono, indipendente dall'ampiezza dello spostamento e dalla frequenza con cui varia l'oscillazione. Allora la velocità sarà dipendente esclusivamente dal materiale attraversato quindi , dato un mezzo elastico e massivo , all'interno dello stesso le onde si propagano con una velocità caratteristica del mezzo stesso. La velocità c nell'aria è praticamente costante ( anche se varia debolmente con la temperatura ) e corrisponde a circa 343 m/s.
Per considerare l'origine fisica del suono consideriamo un sistema fisicamente semplice, costituito da un pistone che oscilla periodicamente grazie ad un albero rotante ( fig. 5 ).
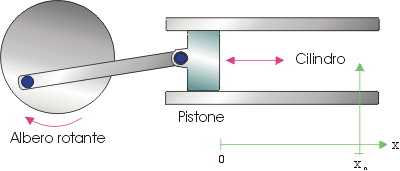
Fig. 5 Pistone con albero rotante
Questo pistone fluttua avanti e indietro spingendo le particelle di aria che sono all'interno del cilindro. Dalla fluidodinamica sappiamo che la prima molecola d'aria segue la stessa legge del moto del pistone. Questo sistema genera onde meccaniche di tipo longitudinale (cioè simili alle onde sonore), e ci permette di capire la dinamica con la quale tali onde si propagano. Se l'albero rotante si muove con velocità angolare w , il moto del pistone sarà di tipo armonico con oscillazioni di ampiezza sinusoidale date dalla seguente legge ( A indica il raggio dell'albero rotante, e X(t ) la posizione del pistone rispetto alla posizione iniziale):
![]() (1)
(1)
La legge del moto è altrettanto valida utilizzando il coseno nella formula ( 1 ) e la scelta dell'uno o dell'altro è esclusivamente determinata dalla posizione iniziale del pistone. Possiamo rappresentare graficamente questa legge con il seguente grafico ( fig. 6 )
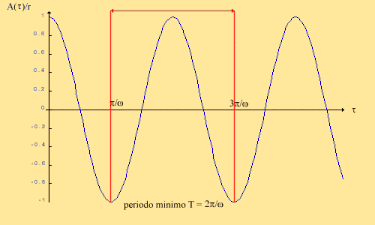
Fig. 6 - Grafico delle oscillazioni in dipendenza dal tempo
Per tale tipologia di moto sono definite tre grandezze, il periodo T e la frequenza f. Il primo ( si misura in secondi, s ) è il tempo impiegato, nel nostro caso, dal pistone ad effettuare un'intera rotazione; la seconda (si misura in hertz, Hz ) è il reciproco del periodo. Per la frequenza non è possibile utilizzare [ 1/s ] come unità di misura perché per il S.I. la grandezza specifica va utilizzata con il proprio nome. La terza grandezza utilizzata è l'ampiezza A che corrisponde al raggio del pistone e avrà come unità di misura i metri ,anche se intuitivamente avrà valori comunque piccoli.
La velocità delle particelle u sarà derivabile matematicamente, e non ha nulla a che vedere con c , infatti nel momento in cui si sposta la particella d'aria l'energia dell'onda è già passata. Quindi si può dire che la velocità del movimento è diversa dalla velocità di movimento . Come già osservato prima l’aria immediatamente a contatto con la parete del pistone, per l’ipotesi di aderenza, segue il moto del pistone, si muove perciò alla stessa velocità che esplicitiamo derivando la (1) rispetto al tempo e ottenendo:
![]() (2)
(2)
La velocità delle particelle è quindi di tipo sinusoidale con valor medio nullo, il che significa che le particelle più vicine al pistone si muovono avanti e indietro nel tubo rimanendo aderenti al pistone.
Si può osservare che ,passando da una funzione seno ad una funzione coseno, quando si ha massimo spostamento la velocità è minima e viceversa quando lo spostamento è minimo la velocità è massima. La (2) è detta legge del moto armonico. Continuiamo lo studio su questo andamento, anche se non tutti i moti sono di questo tipo.
Derivando la velocità posso ottenere l'accelerazione a , funzione sempre sinusoidale e coerente con la legge del moto armonico.
![]() (3)
(3)
L' ![]() che viene fuori a causa della derivazione della funzione seno è un termine proporzionale alla frequenza. Con le considerazioni fatte possiamo osservare che a frequenze molto basse lo spostamento tende ad essere molto piccolo e la velocità u sarà sempre molto inferiore rispetto alla velocità della luce c.
che viene fuori a causa della derivazione della funzione seno è un termine proporzionale alla frequenza. Con le considerazioni fatte possiamo osservare che a frequenze molto basse lo spostamento tende ad essere molto piccolo e la velocità u sarà sempre molto inferiore rispetto alla velocità della luce c.
Andamento spaziale del suono
Considerando l'esempio del pistone e il concetto di mezzo elastico e massivo, andando a osservare l'andamento del moto da un punto distante xn dallo stantuffo, noteremo che lo strato di particelle aderenti al pistone agisce elasticamente trasmettendo la spinta al secondo strato dopo un certo istante di tempo; quindi l'energia meccanica, in altre parole ( per analogia ) l'onda sonora, non si propaga a velocità infinita ma con la velocità c che è stata definita prima. La velocità della generica particella ( che, è importante ripeterlo, non è la velocità dell'onda ) presente nel tubo in corrispondenza dell'ascissa x è ricavabile tramite una traslazione nel tempo della legge vista in precedenza:
![]() (4)
(4)
La traslazione xn/c non è altro che il tempo necessario per percorrere la distanza xn. La formula (4) prende il nome di Onda di propagazione del suono.Il ritardo applicato nel caso di un segnale acustico è un fattore spesso trascurabile, e si può dimostrare attraverso un esempio pratico :
Prendiamo un aula universitaria lunga 13 metri ed una persona che parla dal fondo della stanza matematicamente il ritardo sarà :
![]()
Come si vede benissimo, anche attraverso le normali esperienze, questo tempo non è tale da far sembrare il suono ed il movimento delle labbra fuori sincronia, ma ponendoci in un contesto di distanza molto più alta, e contando sul fatto che normalmente un uomo parlando pronuncia 3 sillabe al secondo, in una distanza dieci volte più ampia della precedente ( 130 m ) notiamo un ritardo matematico di :
![]()
e quindi uno sfasamento di circa una sillaba. In realtà il valore qui sopra ricavato si riferisce al ritardo della sola onda sonora diretta e non a quello degli innumerevoli effetti di riflessione e riverberazione presenti negli ambienti chiusi, che in generale possiedono un ritardo maggiore rispetto all'onda diretta. La voce della persona arriverebbe quindi all'orecchio dell'ascoltatore con una sorta di coda sonora derivante dalla somma degli effetti già citati.
Riprendendo la formula (4) e sviluppando il prodotto all'interno dell'argomento del seno ottengo:
![]() ( 5 )
( 5 )
![]() ( 6 )
( 6 )
Dove è stata introdotta la nuova grandezza k , chiamata numero d'onda e ha come unità di misura [ m –1 ] , quindi non è un numero puro. Ovviamente k può assumere anche valori negativi, ed in questo caso parleremo di anticipo nel segnale.
Che legame c'è tra w e f ? La prima è la pulsazione, cioè il numero di radianti al secondo e poiché per fare un giro completo ci sono 2p radianti :
w
=2p f ( 7 )
Lunghezza d'onda
Supponiamo ora di fare una fotografia istantanea del pistone nel momento in cui è nella massima escursione verso destra, la velocità sarà nulla e man mano che mi sposto verso destra troverò prima la situazione con velocità massima e l'escursione nulla ( x1 ) e poi nuovamente la situazione iniziale ( x3 ) e cosi via:
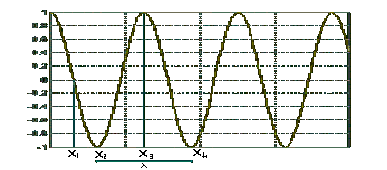
Fig. 6 - Funzione di tipo sinusoidale
Si nota subito che essa assume lo stesso valore sia in x2 che in x4, e questa distanza viene definita lunghezza d'onda (e viene solitamente indicata con la lettera greca lambda, l ): la minima distanza fra due punti che assumono lo stesso valore in un determinato istante. Se noi invece fotografassimo l'onda in un punto x = x1, avremmo ancora una sinusoide, anche se in funzione dello spazio. E così come il periodo indica un'oscillazione completa nel tempo, così la lunghezza d'onda rappresenta un'oscillazione completa nello spazio.
La relazione che c'è tra l e f sarà di tipo inverso:
![]() ( 8 )
( 8 )
e quindi per frequenze alte avremo lunghezze d'onda sempre più piccole. Nella tabella successiva sono illustrate le relazioni tra alcune frequenze e lunghezze d'onda in aria:
|
f |
l [m] |
|
20 |
17 |
|
1000 |
0,34 |
|
20000 |
0,017 |
Tab 1:valori di frequenza con le rispettive lunghezze d'onda
E' importante ora definire il campo d'azione di queste grandezze, ossia il campo di frequenza e la normativa italiana prevede di classificare un suono in un range compreso tra le frequenze di 20 e 20000 Hz . In realtà l'intervallo è leggermente più alto, perché si considerano i centri delle bande, inoltre questo dato per l'uomo è soggettivo e varia con l'età producendo un calo nelle frequenze maggiori.
Una delle osservazioni più interessante è il range di valori elevato ( tre decadi ), dando così origine ad un gran numero molto di lunghezze d'onda, a differenza per esempio di quelle per la luce che oscillano tra i 0,4¸ 0,7 nm. Trattando la luce è quindi possibile definire un valore intermedio di riferimento, mentre per le onde sonore questo non è possibile a causa della banda elevata di frequenza, in quanto il comportamento del suono varia sensibilmente al variare della lunghezza d'onda.Prendiamo per esempio un cubo di lato 1 m per schermare un'onda sonora, sarà sufficiente per qualsiasi tipo di onda? ( fig.7 )
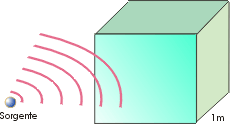
Fig.7: Cubo investito da un’onda sonora
Utilizzando i valori della tabella 1 vedrò che il segnale per basse frequenze passerà inalterato, per alte frequenze sarà bloccato dall'ostacolo e per frequenze intermedio ( che mi danno valori di l dello stesso ordine di grandezza dell'ostacolo ) avrò vari fenomeni di disturbo del segnale.
Pressione sonora
Abbiamo precedentemente detto che affinchè il suono possa diffondersi, il mezzo attraverso cui viaggiano le onde sonore deve essere elastico. Ritornando al caso del pistone mobile, possiamo dire che, dal momento che l'aria è un mezzo elastico, la sua compressione, dovuta all'avanzata del pistone, viaggia con velocità finita e quindi, ad un determinato istante di tempo e ad una opportuna distanza dal pistone, esisterà sempre uno strato di particelle rimaste ferme che costituisce una barriera all'avanzamento delle particelle perturbate dal moto del pistone. Si ha il cosiddetto fenomeno di confinamento inerziale il quale fa sì che, sebbene non vi sia una parete solida, il volume del gas diminuisca e che di conseguenza aumenti la pressione. Quando il pistone torna indietro, il volume e la pressione ritornano ai loro valori originari; possiamo quindi affermare che anche la pressione segue il moto del pistone fluttuando nel tempo con legge sinusoidale.Ricordando il significato energetico e cinetico del suono, osserviamo che al contatto con un mezzo ho il passaggio da energia cinetica ( movimento delle masse ) ad energia potenziale , sotto forma di pressione. In ogni istante l'energia posseduta è sempre la stessa e sarà la somma delle due.Se considero un elemento di aria ad una distanza r ( fig. 8a ), ho una compressione di questo volumetto ( fenomeno piuttosto rapido ) e posso considerare la trasformazione di energia adiabatica e quindi varrà la legge:
PVg =cost ( 9 )
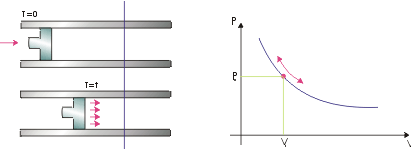
Fig.8 :compressione del pistone e relativo grafico di oscillazione
Il sistema , seguendo questa legge, oscillerà intorno al punto ( P0,V0 ) , cioè intorno alla pressione atmosferica.
Chiameremo Pressione sonora P' la differenza tra la pressione complessiva che fluttua nel tempo P (t ) meno il valore costante dato dalla pressione atmosferica P0.
P’ = P(t ) - P0 ( 10 )
Poiché si tratta di una grandezza relativa, cioè calcolata a partire da un valore di riferimento costante, che in questo caso è la pressione atmosferica media, può assumere anche valori negativi. Le pressioni coinvolte in campo sonoro sono sempre molto piccole. Si raggiunge una pressione di 1 Pa quando il suono ha un livello in decibel pari a 94 dB che è un valore superiore a quello della voce umana. Le due equazioni fondamentali che descrivono la fluttuazione di pressione sonora sono:
PV=RT ( 11 )
PVg =P0V0g ( 12 )
Da cui:
P
r -g =P0r 0-g ( 13 )P=P0
r 0-g r g ( 14 )
Dunque vedo che la pressione non cresce linearmente con la densità ma cresce con una sua potenza. Posso calcolarmi la pendenza di questa curva effettuandone la derivata:
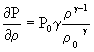 ( 15 )
( 15 )
Se calcoliamo il valore locale nell’origine ( 15 ) , nell’ipotesi di piccoli spostamenti, otteniamo la pendenza della curva in quel punto, e sarà quindi possibile approssimare la curva con una retta.
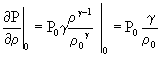 ( 16 )
( 16 )
In particolare scopriamo che questa derivata ha come dimensione quella di una velocità elevata al quadrato, infatti ricordando l’equazione di Bernoulli e che la velocità è quella del suono otteniamo:
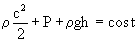
![]()
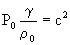
E’ possibile ora esplicitare la velocità :
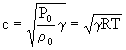 ( 17 )
( 17 )
La velocità di propagazione dipende solo dal mezzo e non dall’ampiezza e frequenza del segnale ed è invece dipendente dalla temperatura. Questa relazione è alla base della Termometria acustica, e sarà possibile così misurare per esempio la temperatura in una camera di compressione misurando il tempo di propagazione nel mezzo. Nei liquidi valgono relazioni analoghe:
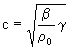 ( 18 )
( 18 )
dove b è il modulo di compressibilità isoterma e vale:
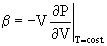 ( 19 )
( 19 )
Questo modulo ha un valore elevato e avremo una velocità di propagazione maggiore rispetto a quella dell’aria. Nella tabella 2 sono illustrate alcune tra le velocità di propagazione riferite ai mezzi più usati:
|
Mezzo |
Velocità del suono [m/s] |
|
Quarzo |
5486 |
|
Acciaio |
6096 |
|
Azoto (a 27°C e 1 BAR) |
355 |
|
Azoto (a 27°C e 100 BAR) |
379 |
|
Mercurio |
1451 |
|
Glicerina |
1895 |
|
Idrogeno |
1281 |
|
Elio |
600 |
Tabella 1 – Valore della velocità del suono in vari mezzi
Osserviamo che l’azoto non può essere considerato un gas perfetto perché la velocità del suono varia con la pressione.E' importante notare l'alto valore dell'acqua; oltre ad essere abbastanza elevato, l'acqua ha un bassissimo coefficiente di perdita: il suono infatti può percorrere in acqua anche centinaia di chilometri prima di perdere ampiezza. Questa velocità ha anche un aspetto negativo: infatti il tempo necessario a raggiungere un orecchio è pressoché uguale a quello necessario a raggiungere l'altro. Questo non ci permette, in acqua, di localizzare correttamente l'origine dei suoni. Il nostro sistema uditivo è infatti "calibrato" per ascoltare suoni provenienti dall'aria: in base al ritardo che impiega un suono a giungere alle nostre orecchie (IDT, interaural delay time o ILD, interaural level difference per le alte frequenze), capiamo da dove arriva. In acqua, dove la velocità del suono è diversa, il nostro sistema uditivo non riesce a capire dove si trova la sorgente; e però sufficiente utilizzare un dispositivo come quelli utilizzati una volta dai sottomarini per ovviare a questo problema,infatti , essendo la velocità in acqua circa cinque volte quella in aria, è sufficiente che si ascoltino, dall'interno di un involucro grande cinque volte la nostra testa (per mezzo di strumenti chiamati idrofoni) i suoni percepiti agli estremi di tale oggetto; in tale modo, inoltre, si mantiene la proporzione anche con l'effetto schermante della nostra testa. Siamo così in grado di localizzare correttamente l'origine del suono.
Per i solidi infine vale la relazione :
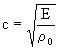 ( 20 )
( 20 )
dove E è il modulo elastico [N/m2].
Osservando i valori della tabella e ricordando la teoria dei modelli si possono fare importanti considerazioni sulla progettazione di prototipi in scala, infatti ricordando la formula:
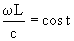 ( 21 )
( 21 )
si può osservare che per lunghezze caratteristiche del modello L molto basse la frequenza d’onda aumenta in maniera eccessiva.Si può risolvere questo problema andando ad utilizzare un fluido che abbia una velocità del suono più bassa di quella dell’aria, permettendomi così di lavorare a frequenze più basse.
Cerchiamo ora di capire il legame tra pressione e velocità. Innanzitutto dobbiamo osservare l’esempio del pendolo, in cui possiamo facilmente osservare i valori di energia potenziale ed energia cinetica, Il pendolo di compressione mostra come ci sia una suddivisione di queste due energie, con particolare attenzione ai due casi limite, il primo è quando il pendolo è nella posizione di equilibrio, in cui l'energia cinetica è massima e l'energia potenziale è nulla, mentre il secondo è nei punti di massima escursione verticale, in cui l'energia cinetica è nulla e l'energia potenziale è massima. Questo comportamento è lo stesso per la coppia pressione-velocità ed andando a diagrammarne l’andamento vedo subito che quando una è massima l’altra è nulla e viceversa. Nell’esempio considerato le funzioni che esprimono la velocità e la pressione sono:
![]()
![]()
|
|
|
Fig.9 :Pendolo di compressione e grafico velocità / pressione
Da notare inoltre il paragone dell’andamento di queste due grandezze con la tensione e la corrente in u circuito elettrico, in cui similmente abbiamo due grandezze sfasate. Le funzioni riportate nel grafico non sono necessariamente sinusoidale ne necessariamente con questo ritardo ( sfasamento ). E' possibile fare delle considerazioni sul massimo trasporto di energia che sarà dipendente dal ritardo ( analogamente ai circuiti elettrici ).Nella situazione rappresentata in figura avremo invece trasporto di energia nullo ( le grandezze sono sfasate di 90° ) e all’interno del tubo avrò un campo stazionario e otterrò delle onde stazionarie.Il massimo trasporto di energia lo avremo invece quando le due grandezze saranno in fase. Da questi due casi "limite" teorici si estrapolano poi i casi reali, con la divisione dell’energia totale tra i due. In generale in ogni onda acustica avremo una quota di campo stazionario e una quota di campo oscillante.