Scambio termico per convezione

La convezione è uno dei tre modi attraverso cui avviene la propagazione del calore. E’ un fenomeno che interessa tipicamente i fluidi e si basa sul trasporto macroscopico di materia.

Se analizziamo ciò che accade durante lo scambio termico tra un solido ed un fluido, ci accorgiamo che esiste uno scambio di tipo conduttivo ed un fenomeno di trasporto di materia; in fig.1 è rappresentato il caso di un fluido che interagisce con una parete solida a temperatura T_p > T_fluido :

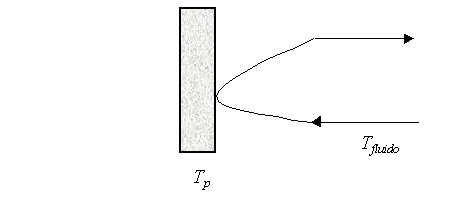
Fig. 1

Inizialmente la parete cede calore per conduzione alle particelle di fluido prossime alle superficie; l’energia così trasmessa va ad aumentare l’energia interna del fluido ed è portata via dal movimento del fluido stesso. Quando le particelle riscaldate raggiungono una regione a temperatura minore trasmettono, ancora per conduzione, del calore alle particelle più fredde.

In questo caso il moto del fluido è dovuto alla differenza di densità che si instaura tra diverse porzioni del fluido stesso a causa delle variazioni di temperatura a cui è sottoposto.

Questo meccanismo è tipico della cosiddetta convezione naturale che ha luogo ogni qualvolta un corpo viene posto in un fluido a temperatura maggiore o minore di quella del corpo stesso. Lo scambio termico che si instaura tra corpo e fluido provoca variazioni nella densità delle porzioni di fluido che si trovano nelle immediate vicinanze della superficie del corpo; le parti più pesanti tendono così ad andare verso il basso mentre quelle più leggere a salire, creando una corrente fluida (moto convettivo) con relativo trasporto di calore.

Questo fenomeno è alla base del funzionamento dei “termosifoni” (o corpi scaldanti) dove l’aria fredda, passando attraverso le lamelle, si scalda e va verso l’alto.

Diversa è la metodologia di realizzazione della convezione forzata dove entra in gioco un fattore esterno (come una pompa o un ventilatore); le correnti convettive vengono create artificialmente ed è necessario spendere del lavoro per mantenere il trasporto di calore. Il raffreddamento di un radiatore di un automobile con aria soffiatavi sopra da una ventola ne è un esempio.

Molto spesso i due fenomeni si intrecciano dando luogo alla convezione mista: è il caso del ventilconvettore dove una ventola spinge l’aria fredda attraverso le lamelle di un corpo scaldante. È importante notare che la ventola è solo un surplus il cui effetto si sovrappone alla convezione naturale che si avrebbe in ogni caso.

Lo scambio termico convettivo è quindi strettamente legato al moto del fluido ed affonda le sue radici nella trattazione termodinamica.

Come sappiamo un fluido si può muovere di moto laminare o turbolento.

Nel primo caso il fluido si muove a strati ed ogni particella procede con un cammino continuo e regolare senza mescolarsi con gli strati adiacenti.

Nel turbolento invece le particelle hanno un cammino irregolare, a zig-zag, del tutto caotico; è importante notare, però, che dal punto di vista statistico il loro moto è regolare e prevedibile.

Entrambi i moti non sono vincolati ad una specie di convezione piuttosto che ad un’altra. La tabella mostra che sia il moto laminare che quello turbolento possono verificarsi in tutti e tre i tipi di convezione.

Naturale	x	x
Forzata	x	x
Mista	x	x
	Laminare	Turbolento

Fig. 2

La massima efficacia di scambio termico si ottiene con convezione forzata in regime turbolento mentre la minima con convezione naturale in regime laminare.

Nel moto turbolento il meccanismo di trasporto del calore è favorito dalla presenza di vortici che trasportano gruppi di particelle di fluido attraverso le linee di corrente; queste particelle agiscono come trasportatori di energia, la quale viene trasmessa tramite il mescolamento con altre porzioni di fluido. Quindi un incremento della velocità di mescolamento (ovvero della turbolenza), magari tramite un agente esterno (forzata), causerà anche l’aumento della potenza termica trasmessa per convezione.

Quando invece un fluido si muove di moto laminare lungo una superficie avente una temperatura diversa, il calore si trasmette soltanto per conduzione sia all’interno del fluido, su scala molecolare, sia all’interfaccia solido-liquido e la mancanza di vortici ne penalizza la resa convettiva.

Un’ altro fattore che influisce sulla resa convettiva è il calore specifico del fluido utilizzato. Infatti un fluido con basso calore specifico riesce a “portare via” poca energia e quindi il fenomeno viene penalizzato.

Questo spiega perché il raffreddamento ad acqua in ambito meccanico è migliore rispetto ad uno ad aria; l’acqua ha un calore specifico che è circa 4,187 volte quello dell’aria e quindi, a parità di kg di sostanza, “porta via” più calore.

In ambito elettronico esistono alcune applicazioni che utilizzano anche il raffreddamento ad olio , come i trasformatori elettrici di grandi dimensioni: l’olio infatti è un materiale che ha un’ottima costante dielettrica (funziona da isolante elettrico) e inoltre ha una capacità di trasporto del calore che è molto maggiore di quella dell’aria.

Dal punto di vista matematico lo scambio termico per convezione sarebbe teoricamente studiabile modificando l’equazione di Fourier con un “trucco” già utilizzato nel campo del moto dei fluidi.

Sappiamo che nell’ipotesi di fluido fermo vale la seguente legge:

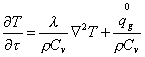
(1)

dove = a = diffusività.

Se il fluido si muove possiamo sostituire (come nell’equazione di Navier ) il simbolo di derivata parziale con quello di derivata sostanziale:

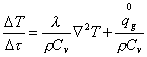
(2).

In questo modo viene rappresentato il moto incomprimibile in cui il volume specifico non varia sensibilmente , quindi possiamo trascurare il lavoro di espansione (considerando r costante).

In realtà r = r₀ + r’ , ma la sua variazione è trascurabile rispetto al valore medio sotto l’ipotesi di piccole variazioni di temperatura.

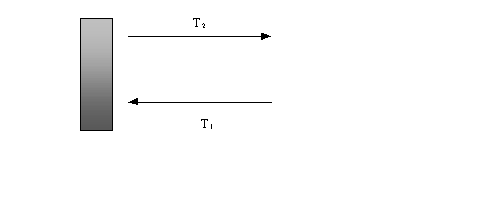
Fig. 3

Se ci riferiamo alla fig.3 , dove un gas lambisce la parete ad una temperatura T₁ e si allontana ad una temperatura T₂ , si dovrà avere ,

cioè variazioni di temperatura dell’ordine di qualche di gradi kelvin.

Ma la sola equazione di Fourier non è sufficiente per descrivere completamente il fenomeno in quanto fornisce le cause ma non riesce a descriverne gli effetti.

In generale la trattazione di un problema convettivo richiede la simultanea risoluzione dell’equazione di Fourier e di quella di Navier , accoppiate tramite quella di continuità (per la densità variabile): in regime di convezione forzata la situazione si presenta più semplice in quanto le due equazioni risultano disaccoppiate.

Nonostante questo la soluzione simultanea delle due equazioni è irrealizzabile nella stragrande maggioranza dei casi e solo nei laboratori di Los Alamos negli Stati Uniti si continua a cercarne la soluzione.

Nell’ambito ingegneristico si preferisce usare altri metodi per calcolare la convezione; dal punto di vista quantitativo si può dare una stima del fenomeno definendo il cosiddetto coefficiente di convezione attraverso la seguente relazione;

(3)

dove q è la potenza termica , è la temperatura della parete , quella del fluido lontano dalla parete e h è il suddetto coefficiente.

Poiché , cioè è una variabile spazio-temporale che varia da punto a punto , ne si definisce un valore medio spaziale (quando si ha a che fare con grandi superfici S ) :

(4)

dove (5)

è definito come integrale sulla superficie S del valore locale di h.

Dal punto di vista teorico risolvere un problema di scambio termico convettivo significa determinare il valore del coefficiente di convezione.

Ma il valore di h non è ottenibile attraverso una equazione di analisi , bensì utilizzando la cosiddetta analisi dimensionale (Teoria dei Modelli) , scienza a sé stante che studia i fenomeni dell’analogia , basandosi sul fatto che

uguali equazioni differenziali uguali risultati.

Fu fondata da Reynolds , il quale fu il primo a teorizzare questa apparente similitudine tra fenomeni fisici diversi , imputabile ad una legge fisica “superiore” (nota come Analogia di Reynolds) , riuscendo a dimostrare matematicamente e a verificare sperimentalmente la validità delle sue ipotesi in un’ equivalenza tra tre fenomeni fisici;

· Moto dei fluidi

· Scambio termico

· Fenomeni di diffusione dei gas

(es. Diffusione in aria degli odori e legge di Fick)

Dimostrata l’equivalenza tra i risultati di questi tre , Reynolds allargò il campo a tutti i fenomeni fisici che vengono studiati seguendo una procedura standard comprendente:

1) Adimensionalizzazione dei fenomeni

Tutte le equazioni che governano il fenomeno vanno scritte in forma adimensionale.

Le grandezze rappresentative del problema vengono manipolate in modo da renderle adimensionali , ossia dei numeri puri.

In tal modo un’equazione scritta con numeri puri diventa invariante rispetto alle dimensioni fisiche del problema; quindi un’equazione matematica scritta con grandezze adimensionali avrà sempre la stessa soluzione , indipendentemente da quale sia il problema fisico considerato.

La soluzione , ovviamente adimensionale , risulterà invariante ; pertanto andrà calcolata solo una volta e ad essa si farà riferimento per tutti i casi resi simili tramite operazioni di analisi dimensionale.

In pratica abbiamo circa 30 – 35 problemi fondamentali la cui soluzione algebrica risulta troppo complessa: per questo motivo , trovata la soluzione per via empirica , sono stati tabulati e divisi in classi secondo varie caratteristiche fondamentali , in modo da poter essere utilizzati come problemi “tipo”.

Parlando di moto dei fluidi (in prossimità di una parete) abbiamo già visto la definizione di una velocità adimensionale e il concetto di strato limite , definito come il luogo dei punti in cui , secondo la relazione;

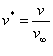(6)

dove è la velocità del fluido lontano dalla parete.

Analizziamo ora lo scambio termico per convezione tra una lastra a temperatura T_p e l’aria circostante che lontano dalla parete si trova alla temperatura T_¥ (con T_¥ > T_p ).

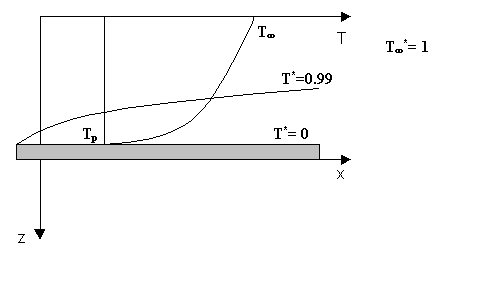
Fig. 4

A contatto con la lastra si crea uno strato limite , luogo dei punti in cui avviene il 99% del salto di temperatura.

In questa esperienza diventa possibile definire una temperatura adimensionale indipendente dai parametri finora adottati con la seguente relazione:

(7)

In questo modo sulla parete si ha = 0 e all’infinito = 1 e la variazione spaziale di è analoga a quella di (cioè le due grandezze adimensionali sono analoghe).

2) Teorema di Buckingham

L’analogia porta con sé cosiddetto Teorema p (o di Buckingham) , simile per certi versi alla regola delle fasi di Gibbs , in quanto stabilisce qual è il numero massimo di variabili indipendenti che governano un problema.

Se applicato ad un problema adimensionale , quindi inquadrato nel concetto dell’analogia di Reynolds , stabilisce che il numero di raggruppamenti adimensionali indipendenti (uno dei quali è appunto il numero di Reynolds , che ne è stato il capostipite) è uguale al

numero di variabili dimensionate ¾ numero di equazioni .

Se ho n equazioni e m variabili il numero di gradi di libertà del sistema è n - m.

Consideriamo un problema che presenta 3 variabili A,B,C tra le quali sussistano due relazioni;

(8)

Il teorema di Buckingham dice che raggruppamento adimensionale che può variare in maniera indipendente; non dice qual è , in quanto è la fisica del problema o l’analogia di Reynolds che lo caratterizza.

Possiamo chiamarlo , cioè funzione delle tre variabili ed unica vera variabile del fenomeno, come la era il numero di Reynolds nel caso del moto di un fluido dentro un tubo.

Lo stesso procedimento si applica anche allo scambio termico; mettendoci nel caso più complesso possibile , quindi in presenza di convezione forzata e moto turbolento e volendo valutare il valore locale del coefficiente di convezione (quello medio introdurrebbe un’ ulteriore equazione) , il teorema di Buckingham dice che il numero di numeri puri indipendenti possibili è 4.

Adimensionalizzando le cinque equazioni a nostra disposizione (cioè le tre di Navier, quella di Fourier e quella di continuità) otteniamo 5 variabili adimensionali;

1. N_u numero di Nusselt

2. R_e numero di Reynolds

3. G_r numero di Grashof

4. P_r numero di Prandtl

5. X/L ascissa adimensionale (posizionatore).

Il teorema p dice che dovrebbero essere 4 e non 5 Þ deve esistere una relazione formale che esprima uno di questi numeri in funzione degli altri quattro.

Normalmente si esprime N_u come;

(9)

dove L è la lunghezza caratteristica (per un liquido che scorre dentro un tubo è il diametro) la cui scelta dipende da vari fattori; di solito si adotta la definizione data dallo scienziato che ha studiato il problema.

Formalmente la soluzione di un problema convettivo si esprime dicendo che ; noti i valori delle quattro variabili , che dipendono dai dati di ingresso e nota la funzione f che esiste tabellata su libri specifici (ricavata con esperimenti) , si calcola il valore di N_u (coefficiente adimensionalizzato di convezione) e si ricava quello di h utilizzando la (9).

Definiamo ora gli altri 4 numeri puri;

(10)

(11)

dove w è la velocità e è la viscosità

(12)

dove g è l’accelerazione di gravità , b è il coefficiente di dilatazione termica del gas definito come (13)

ed esprime l’incremento percentuale di volume causato da una variazione di temperatura di 1^° C.

Poiché per un gas perfetto vale l’equazione , ricavando e sostituendo nella (13) si ottiene (14)

(Þ si misura in K^-1) valido solo per un gas a temperatura T.

Per i liquidi b è variabile e può assumere anche valori negativi.

(15)

in quanto a = diffusività = .

Dopo averli definiti cerchiamo di capirne il significato fisico.

Ciascuno di questi numeri può essere visto come un rapporto.

e dà un’idea del “motore” che produce la convezione naturale (legata all’accelerazione di gravità).

intendendo “diffusione” come propagazione spaziale.

Il numero di Prandtl ha un preciso significato fisico nel caso dello sviluppo degli strati limite (termico e dinamico) a contatto con una superficie; in questo caso dà una misura di “quanto lontano” dalla parete arriva la perturbazione fluidodinamica o quella termica.

In particolare quando

Þ gli effetti termici si estendono a maggior distanza di quelli fluidodinamici

Þ prevalgono gli effetti termodinamici.

Per l’acqua ad esempio quindi l’effetto della superficie è maggiore dal punto di vista termodinamico.

Tornando all’aspetto operativo della trattazione , le formule che esprimono N_u

in funzione degli altri quattro parametri sono solitamente espresse come prodotto fra potenze.

Infatti l’espressione generica è data da

(16)

e ogni formula implica

.