Proprietà dei gas perfetti e dei vapori surriscaldati

Vapori surriscaldati
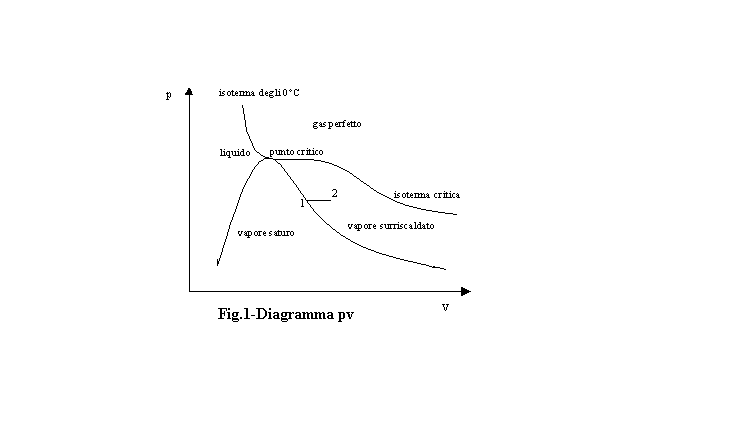
Nella zona del diagramma pv compresa tra l’isoterma critica e la curva limite superiore vi sono i vapori surriscaldati, caratterizzati, rispetto ai vapori saturi, da temperature più elevate, sono molto rarefatti e, pertanto, sono molto simili ai gas perfetti, pur essendo sotto l’isoterma critica. Difatti, se, ad esempio, mi voglio calcolare l’entropia specifica di un vapore surriscaldato, mi prendo (come in figura 1) un punto 2 appena fuori dalla curva limite e lo collego con un punto 1 sulla curva, in maniera da avere una trasformazione a pressione costante. In tal caso vale l’equazione
![]()
Dunque, conoscendo p2 mi posso ricavare la temperatura nel punto 2 dalle tabelle del vapore saturo e, quindi, l’ entalpia, dato che anche il cp lo posso ottenere dalle apposite tabelle. Tuttavia, se il punto 2 è sufficientemente vicino al punto 1, posso andare a prendere come cp il calore a pressione costante nel punto 1, in caso contrario vado a considerare il ![]() , ovvero il cp medio.
, ovvero il cp medio.
Conoscendo l’entalpia h posso facilmente calcolarmi l’energia interna u2, considerando che
![]() ,
,
e l’entropia s2, dalla relazione ![]() e quindi, visto che sto operando a p costante ,
e quindi, visto che sto operando a p costante ,
![]() .
.
Più semplicemente mi posso ricavare entalpia, entropia ed energia libera dalle apposite tabelle per i vapori surriscaldati. Queste tabelle sono dette a doppia entrata perché alla scelta dei valori di p e T, troviamo quelli di v,h, u, s, oppure di cp e cv.
Di seguito c’è un esempio di tabella a doppia entrata, che riporta i valori caratteristici del vapore d’acqua surriscaldato nell’intervallo di temperature tra 120 e 650°C e a sottoposto a pressioni di 1,2, 1,4, 1,6 bar:
|
P (bar) |
1,2 |
1,4 |
1,6 |
|||||||
|
t (°C) |
T (K) |
H |
S |
V |
H |
S |
V |
H |
S |
V |
|
120 |
393,15 |
2714,4 |
7,3787 |
1490,1 |
2712,3 |
7,3033 |
1274,0 |
2710,1 |
7,2373 |
1111,9 |
|
140 |
413,15 |
2754,7 |
7,4788 |
1570,8 |
2753,0 |
7,4044 |
1343,7 |
2751,3 |
7,3395 |
1173,4 |
|
160 |
433,15 |
2794,8 |
7,5734 |
1650,5 |
2793,4 |
7,4998 |
1412,5 |
2792,0 |
7,4356 |
1234,0 |
|
180 |
453,15 |
2834,6 |
7,6634 |
1729,7 |
2833,5 |
7,5903 |
1480,7 |
2832,3 |
7,5266 |
1293,9 |
|
200 |
473,15 |
2874,4 |
7,7492 |
1808,4 |
2873,4 |
7,6765 |
1548,4 |
2872,5 |
7,6133 |
1353,4 |
|
220 |
493,15 |
2914,1 |
7,8315 |
1886,7 |
2913,3 |
7,7591 |
1615,7 |
2912,5 |
7,6962 |
1412,5 |
|
240 |
513,15 |
2953,9 |
7,9106 |
1964,7 |
2953,2 |
7,8384 |
1682,8 |
2952,5 |
7,7758 |
1471,3 |
|
260 |
533,15 |
2993,8 |
7,9869 |
2042,6 |
2993,2 |
7,9149 |
1749,7 |
2992,6 |
7,8524 |
1530,0 |
|
280 |
553,15 |
3033,8 |
8,0605 |
2120,3 |
3033,3 |
7,9887 |
1816,4 |
3032,7 |
7,9263 |
1588,5 |
|
300 |
573,15 |
3074,0 |
8,1319 |
2197,9 |
3073,5 |
8,0601 |
1883,0 |
3073,0 |
7,9979 |
1646,8 |
|
350 |
623,15 |
3175,3 |
8,3012 |
2391,5 |
3174,4 |
8,2297 |
2049,1 |
3174,5 |
8,1676 |
1792,3 |
|
400 |
673,15 |
3277,9 |
8,4597 |
2584,7 |
3277,6 |
8,3882 |
2214,9 |
3277,3 |
8,3263 |
1937,5 |
|
450 |
723,15 |
3382,1 |
8,6090 |
2777,7 |
3381,8 |
8,5376 |
2380,4 |
3381,6 |
8,4757 |
2082,4 |
|
500 |
773,15 |
3487,9 |
8,7505 |
2970,6 |
3487,7 |
8,6791 |
2545,8 |
3487,5 |
8,6173 |
2227,3 |
|
550 |
823,15 |
3595,4 |
8,8852 |
3163,4 |
3595,2 |
8,8139 |
2711,1 |
3595,0 |
8,7521 |
2371,9 |
|
600 |
873,15 |
3704,6 |
9,0140 |
3356,1 |
3704,5 |
8,9427 |
2876,4 |
3704,3 |
8,8809 |
2516,6 |
|
650 |
923,15 |
3815,5 |
9,1375 |
3548,7 |
3815,4 |
9,0662 |
3041,5 |
3815.2 |
9,0045 |
2661,1 |
![]()
Gas perfetti
Nel diagramma pv i gas perfetti occupano la regione di piano al di sopra dell’isoterma critica, essendo caratterizzati da pressioni e temperature elevate.
Più precisamente questi gas, a meno di un errore accettabile, giacciono sulla superficie che obbedisce all’" equazione di stato dei gas perfetti " ovvero:
![]()
e, quindi, hanno le isoterme rappresentabili come iperboli equilatere (fig.2) 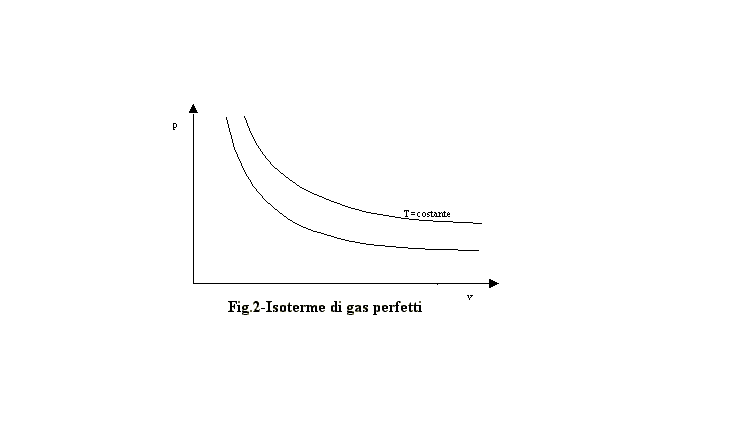
I parametri componenti l’equazione precedente sono p, la pressione misurata in Pascal, v, che rappresenta il volume specifico e viene misurato in![]() , T, la temperatura espressa in gradi Kelvin, ed R0, che è la costante universale dei gas e dipende dalle grandezze con cui operiamo.
, T, la temperatura espressa in gradi Kelvin, ed R0, che è la costante universale dei gas e dipende dalle grandezze con cui operiamo.
Dal principio di Avogadro sappiamo che una mole di qualsiasi gas perfetto occupa sempre lo stesso volume: allora, da un punto di vista chimico, l’equazione dei gas diventa
![]() ,
,
dove il volume molare, per i gas ideali a 273,15 K( 0 °C) e 1 atm,
Vm = (volume V)/(numero di moli n)![]() , e allora
, e allora
R0 ![]() .
.
Ma se volessi questa costante espressa non in funzione del numero di moli, ma della massa molare m (massa in kg contenuti in un kmol di sostanza), allora avrei la costante caratteristica dei gas
R![]() ,
,
visto che ![]() (1) e moltiplicando per m entrambi i membri dell’equazione di stato dei gas avrò
(1) e moltiplicando per m entrambi i membri dell’equazione di stato dei gas avrò ![]() , allora ho
, allora ho ![]() (2) e, dunque, confrontando la (1) con la (2) avrò come affermato in precedenza R
(2) e, dunque, confrontando la (1) con la (2) avrò come affermato in precedenza R![]() .
.
Nella tabella seguente vi sono la massa molare m e la costante R di alcune sostanze:
|
SOSTANZA |
m (kg/kmol) |
R (J/kg K) |
|
Acetilene, C2H2 |
26,039 |
319,43 |
|
Acqua, H2O |
18,016 |
461,70 |
|
Ammoniaca, NH3 |
17,032 |
488,38 |
|
Anidride carbonica, CO2 |
44,012 |
188,99 |
|
Anidride solforosa, SO2 |
64,066 |
129,83 |
|
Argon, Ar |
39,950 |
208,21 |
|
Aria |
28,968 |
287,13 |
|
Azoto, N2 |
28,014 |
296,91 |
|
Elio, He |
4,0028 |
2078,0 |
|
Etano, C2H6 |
30,071 |
276,60 |
|
Etilene, C2H4 |
28,055 |
296,48 |
|
Freon, 12CCl2F2 |
120,914 |
68,77 |
|
Idrogeno, H2 |
2,0158 |
4126,4 |
|
Metano, CH4 |
16,044 |
518,46 |
|
Neon, Ne |
20,184 |
412,10 |
|
n-Butano, C4H10 |
58,124 |
143,04 |
|
Ossido di azoto, NO |
30,007 |
277,19 |
|
Ossido di carbonio, CO |
28,012 |
296,93 |
|
Ossigeno, O2 |
31,891 |
260,83 |
|
Propano, C3H8 |
44,097 |
188,50 |
Dalla tabella osserviamo che nella teoria dei gas perfetti l’aria viene considerata un sistema chimicamente omogeneo, ma in realtà non è cosi, poiché essa è composta al 21% di ossigeno e al 79% circa di azoto, con la rimanente parte che è costituita da una porzione trascurabile di gas vari. Difatti, se facessi bollire un recipiente pieno di aria liquida, comincerei ad avere un cambiamento di fase ad una temperatura prossima alla temperatura critica dell’azoto (77,36 K o -195,79°C), più bassa di quella dell’ossigeno (90,2 K o -182,95°C), dove avrei la trasformazione in gas dell’azoto e la temperatura rimarrebbe costante finché non mi rimarrà allo stato liquido solo l’ossigeno, dopodiché avrei una risalita fino alla temperatura di ebollizione del liquido rimanente, dove ci sarebbe daccapo un punto dove avverebbe una trasformazione a T costante che mi porterebbe tutto l’ossigeno allo stato gassoso.
Tale processo, denominato distillazione frazionata, mi dimostra come l’aria in realtà non sia un sistema chimicamente omogeneo, ma nella teoria dei gas perfetti lo consideriamo omogeneo ed in quanto tale la massa molare del gas aria sarà la media numerica fra la massa molare dell’ossigeno ( m =![]() ) e quella dell’azoto (m =
) e quella dell’azoto (m =![]() ) e sarà pertanto m
) e sarà pertanto m![]() e, quindi,
e, quindi,
Raria = ![]() .
.
Per i gas perfetti è dimostrabile che
cp-cv=R.
Ma esiste un’altra grandezza che lega cp e cv, è l’esponente di v nell’equazione dell’iperbole equilatera rappresentante la trasformazione adiabatica, e, dunque, isoentropica,
![]() ,
,
rappresentata in fig.3, dove
![]()
![]()
e per un gas perfetto biatomico ![]()
![]() .
.
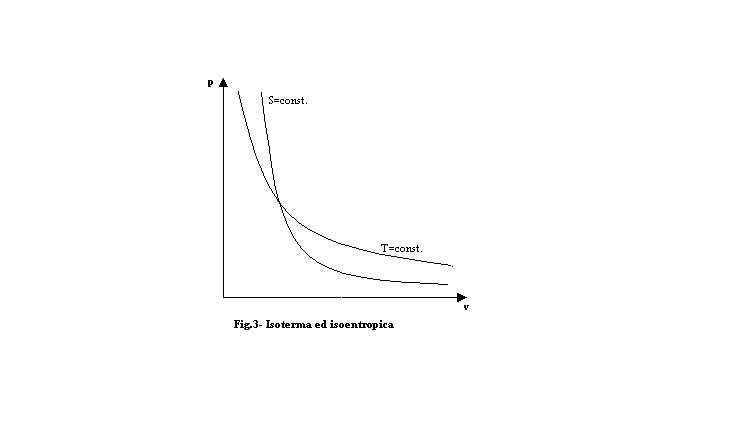
Dal grafico si comprende come l’isoentropica è più ripida dell’isoterma.
Dunque, attraverso ![]() e R posso calcolarmi cp e cv, ma non è sempre così semplice e allora queste due proprietà termodinamiche possono evincersi da varie tabelle, come quella qui sotto, dove sono riportati cp , cv e
e R posso calcolarmi cp e cv, ma non è sempre così semplice e allora queste due proprietà termodinamiche possono evincersi da varie tabelle, come quella qui sotto, dove sono riportati cp , cv e ![]() di alcuni gas alla temperatura di 0°C e pressione di 1 atm:
di alcuni gas alla temperatura di 0°C e pressione di 1 atm:
|
Sostanzacv( |
|
|||
|
Aria |
1,004640 |
0,719992 |
1,40 |
|
|
Ossigeno, O2 |
0,912548 |
0,653016 |
1,40 |
|
|
Azoto, N2 |
1,042314 |
0,745108 |
1,40 |
|
|
Idrogeno, H2 |
14,253330 |
10,130120 |
1,41 |
|
|
Ossido di carbonio, CO |
1,046500 |
0,749294 |
1,40 |
|
|
Anidride carbonica, CO2 |
0,879060 |
0,690690 |
1,27 |
|
|
Vapor d’acqua, H2O |
1,925560 |
1,465100 |
1,30 |
|
|
Anidride solforosa, SO2 |
0,644644 |
0,514878 |
1,25 |
|
|
Ammoniaca, NH3 |
2,218580 |
1,716260 |
1,29 |
|
|
Metano, CH4 |
2,469740 |
1,925560 |
1,28 |
|
Tuttavia, questi valori sono validi a 0°C e pressione di 1 atm, ma, come si può notare nella tabella seguente, dove è analizzato il gas aria a pressione atmosferica, variano, anche se in maniera abbastanza lieve, al crescere della temperatura ed alla conseguente diminuzione di densità :
|
. T(°C) |
|
cp ( |
|
-18 |
1,372 |
1,000454 |
|
0 |
1,296 |
1,004640 |
|
38 |
1,136 |
1,004640 |
|
93 |
0,960 |
1,008826 |
|
149 |
0,832 |
1,017198 |
|
204 |
0,735 |
1,025570 |
|
260 |
0,660 |
1,033942 |
|
316 |
0,597 |
1,046500 |
|
371 |
0,545 |
1,059058 |
|
427 |
0,503 |
1,071616 |
|
482 |
0,465 |
1,084174 |
|
538 |
0,434 |
1,096732 |
|
816 |
0,323 |
1,155336 |
|
1093 |
0,258 |
1,197196 |
|
1371 |
0,213 |
1,222312 |
|
1649 |
0,183 |
1,243242 |
Se sono note una coppia di variabili indipendenti (p,v) o (p,T) allora sono in grado di calcolarmi tutte le altre variabili termodinamiche:
![]() Posso ricavarmi la terza variabile (v o T) della relazione
Posso ricavarmi la terza variabile (v o T) della relazione ![]() .
.
2) L’energia interna u; difatti, essendo u una funzione di stato, essa dipende solo dai suoi valori iniziali e finali. Allora per calcolarmi la variazione di energia libera di una trasformazione da un punto 1 ad un punto 2 mi prendo un a trasformazione isocora dal punto 1 al punto 3 e poi una isoterma (fig.4):
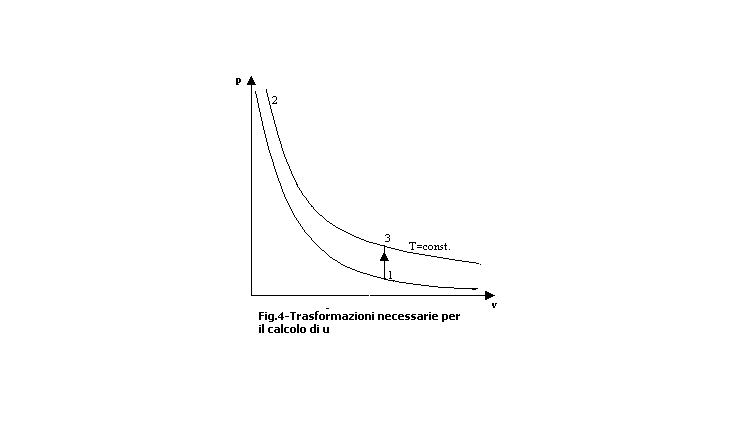
Quindi posso applicare il principio della termodinamica alla trasformazione isocora e avrò:
![]() ,
,
ma, essendo ![]() , allora
, allora
![]() e
e ![]()
e, quindi,
![]() ,
,
ma essendo la trasformazione tra 2 e 3 isoterma posso affermare che
![]()
e, dunque, ponendo la temperatura 0°C come riferimento posso concludere che u![]() (dove t è la temperatura in gradi centigradi).
(dove t è la temperatura in gradi centigradi).
3) Riesco a calcolarmi l’entalpia h operando nella sessa maniera di prima, ma con una trasformazione isobara ed una isoterma (fig.5).
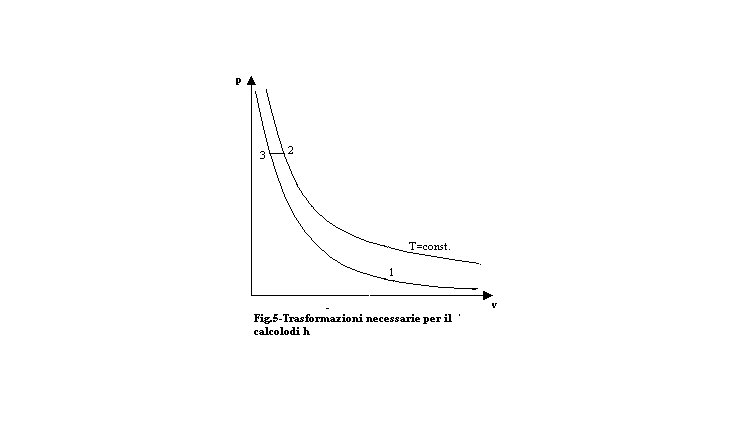
Lungo l’isobara (da 3 a 2) so che
![]()
e pertanto applicando nuovamente il primo principio e tenendo conto dell’isoterma
![]()
e, quindi, integrando tra 1 e 2 ho
h2-h1 = cp(T2-T1)
e riponendo come riferimento la temperatura 0°C ho:
u = cvt e h = cpt
4) Posso trovarmi l’entropia s addirittura in due modi, formulando in maniera differente il primo principio della termodinamica, ed ottenendo due risultati apparentemente diversi, ma sostanzialmente uguali.
Il primo procedimento consiste nell’ applicare il primo principio nella forma differenziale
du = dq-pdv
allora se
du = cvdT
e se , riprendendo la definizione di entropia,
![]()
posso scrivere che
![]()
e, dall’equazione di stato ![]() ,
,
![]()
Integrando, quindi fra lo stato 1 e lo stato 2,
![]()
Il secondo modo consiste nel applicare ancora il primo principio ma nella forma
dh = dq+vdp
allora
![]()
e se
dh = cpdT
e, tenendo conto dell’equazione di stato, posso scrivermi
![]()
Integrando nuovamente:
![]()
Le due forme esprimenti l’entropia s sono equivalenti, con la differenza che una lega s alle variazioni di v e T l’altra alle variazioni di p e T.
Un’altra espressione di s è
![]()
che grazie alle proprietà dei logaritmi posso semplificare:
![]()
e, dunque
![]()
Gas reali
Per i gas reali e i vapori surriscaldati valgono le equazioni di Van der Waals, variazioni dell’equazione di stato, dipendenti da z che è il fattore di comprimibilità dei gas e vale 1 per i gas perfetti
pv = zRT
Dove z è funzione delle coordinate ridotte, che sono pR e TR, coordinate adimensionali riportate al loro valore nel punto critico: (pR = p/pcr ;TR = Tcr).
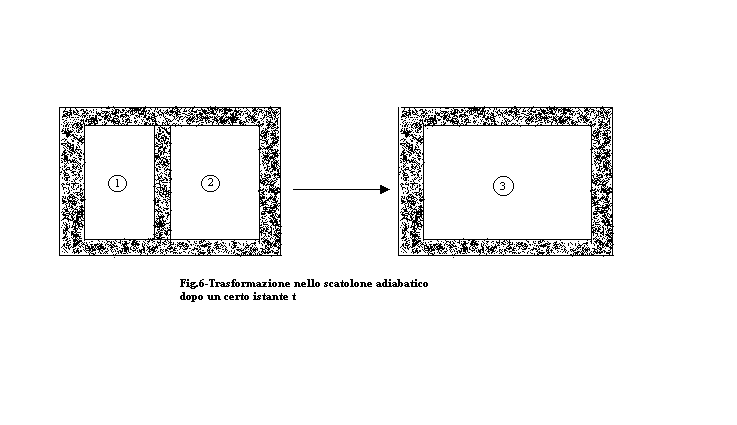
Esercizio : "Scatolone adiabatico"
Lo scatolone adiabatico in figura 6 è un sistema chiuso (v = 0 e, quindi, L = 0) termicamente isolato (Q = 0 ) pieno di aria in cui un setto rigido termicamente isolato separa due porzioni di spazio adiacenti (denominati 1 e 2) . In queste condizioni ho nel primo scomparto 1![]() di aria alla pressione di 1 bar e ad una temperatura T1 = 100°C, nel secondo 2
di aria alla pressione di 1 bar e ad una temperatura T1 = 100°C, nel secondo 2 ![]() di aria alla pressione di 10 bar e ad una temperatura T2 = 200 °C. Se ad un certo istante rimuovo il setto ottengo una miscela delle 2 quantità d’aria.
di aria alla pressione di 10 bar e ad una temperatura T2 = 200 °C. Se ad un certo istante rimuovo il setto ottengo una miscela delle 2 quantità d’aria.
Voglio determinare le condizioni finali nel contenitore (coordinate termodinamiche descriventi lo stato 3) ed un eventuale aumento di entropia al termine del processo.
Soluzione
E’ molto semplice calcolare il volume finale perché è la somma dei due volumi e, quindi, V3 = 3 ![]() .
.
Per ottenere le due incognite p e T ho bisogno di due equazioni: la prima è la conservazione dell'energia libera e cioè,
Ufin = Uin (1)
questo in quanto per definizione L = Q = 0. La seconda equazione mi deriva dal principio di conservazione della massa (essendo il sistema chiuso), difatti ,se v = V/M, ho
p1V1 =M1RT1
che costituisce la terza forma di espressione dell’equazione di stato ( la quarta è pV = nR0T), e, sostituendo i valori delle ipotesi, ho M1 = 0,934 kg e M2 = 14,75 kg, che mi fornisce la massa finale M3 = M1+M2 = 15,68 kg. Quindi, la mia seconda equazione è
p3V3 =M3RT3 (2)
Tenendo conto delle due equazioni e ricordando che l’energia libera specifica
u = U/M = cvT
posso formulare dalla (1) che
M3cvt3 = M1cvt1+ M2cvt2
(con t che costituisce la temperatura centigrada), da cui ho che t3 = 194°C = 467 K.
E’ sostituendomi il valore appena ricavato nella (2) ho che la pressione finale
p3 = 699780,8 Pa![]() 7 bar.
7 bar.
Ho tutte le coordinate termodinamiche finale in maniera tale da potermi caratterizzare lo stato del sistema e comprendere ad esempio che la temperatura finale è molto prossima alla T2, ciò era prevedibile visto che la M2 è molto più grande di M1 e che la T3 rappresenta la media pesata delle temperature di partenza, il cui peso è costituito dalle masse dei due sistemi considerati.
Mi rimane da verificare solamente un eventuale aumento di entropia: tuttavia, una volta rimosso il setto rigido ho un miscuglio delle due quantità iniziali e non sarà più possibile procedere a ritroso e ripristinare le condizioni iniziali, pertanto il processo è irreversibile ed ho sicuramente un aumento di s.
In termini numerici: essendo s una funzione di stato, hanno importanza solo i valori finali ed iniziali e, quindi,![]() S = S3-S1-S2.
S = S3-S1-S2.
Allora considerando T0 = 0°C , p = 1atm e Raria = 287 J/kg K
S1 = M1(cpln![]() -Rarialn
-Rarialn![]() ) = 292,67 J/K
) = 292,67 J/K
Similmente S2 = - 1608 ,04 J/K e S3 = -304,02 J/K.
Quindi, ![]() S = S3-S1-S2 = -304,02+1608,04-292,67 = 1011,35 J/K ed ho, come preventivato, un aumento di entropia.
S = S3-S1-S2 = -304,02+1608,04-292,67 = 1011,35 J/K ed ho, come preventivato, un aumento di entropia.