TRANSITORI TERMICI
Consideriamo una lastra piana con uno spessore S dato e suddividiamola attuando quella che è definita Discretizzazione spaziale.
Con il metodo delle differenze finite introduciamo il passo spaziale:
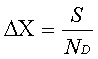
dove S è lo spessore e ND è il numero di divisioni.
La lastra è così divisa in un numero finito di strisce l’una adiacente all’altra. Il punto mediano di ciascuna striscia è chiamato nodo ed in esso si può considerare la temperatura costante.
Normalmente si assume che i nodi partano sulla superficie limite iniziale della lastra e che siano numerati da 0 a ND. Secondo questa notazione avremo dunque ND divisioni e ND+1 nodi.
Ciascun nodo interno è così rappresentativo di una striscia di materiale con spessore DC. Al contrario invece il primo e ultimo nodo sono rappresentativi di una striscia di materiale di spessore DC/2.
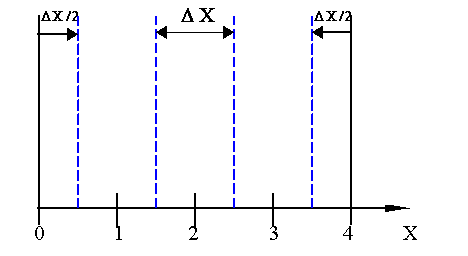
Figura 1- Esempio di
discretizzazione spaziale con cinque nodi e quattro divisioni.
L’ascissa x del nodo n-esimo equivale quindi a:
![]() con
con ![]()
dove n è un numero puro chiamato indice di nodo e rappresenta il puntatore dentro il vettore o la matrice che conterrà le temperature dei nodi. Per questo motivo indicheremo con T1 la temperatura al nodo 1, e con Tn la generica temperatura al nodo n-esimo.
Si può notare che in questo modo la variabile X non è più continua ma assume solo valori discreti.
E’ importante sapere che questa non è però l’unica rappresentazione spaziale possibile. C’è infatti chi parte ponendo il primo nodo appena dentro la pelle della lastra. In questo modo il numero dei nodi equivale a quello delle divisioni e in più anche i nodi esterni sono rappresentativi di una striscia di materiale di spessore DC.
Quale rappresentazione usare è in ogni caso una scelta soggettiva e tale decisione ha portato, tra le varie cose, alla diversa interpretazione di vettori o matrici nei vari linguaggi di programmazione. Infatti per questo motivo ci sono linguaggi in cui il primo posto dei vettori è identificato con il numero 1 mentre altri come il Basic o il Pascal in cui lo stesso è identificato con il numero 0.
Per risolvere i problemi di transitorio bisogna introdurre anche una discretizzazione temporale che è effettuata con un passo temporale costante Dt misurato in secondi.
Tenendo conto delle cose già dette avremo:
![]()
dove t è il tempo corrente e t è un numero puro chiamato indice di tempo.
La soluzione del problema di transitorio si riduce ad essere una matrice bidimensionale discreta in entrambe le direzioni che contiene le temperature dei nodi ai vari istanti esaminati.

Figura 2
- Matrice rappresentativa di un problema
suddiviso in 5 nodi ed esaminato per 7 unità temporali.
Indicheremo quindi con Tnt la generica temperatura al nodo n all’istante t=tDt the occuperà la cella (n,t) nella matrice sopra descritta (Nei linguaggi di programmazione si utilizza in genere la seguente rappresentazione: T(n,t) ,se si usa un linguaggio come il Basic o il Fortran, T[n,t] se invece si usa il Pascal o il C).
Il nostro obbiettivo è riuscire a calcolare i contenuti delle celle della matrice. Come vedremo ciò è possibile attraverso una formula ricorsiva utilizzando la tecnica di time marching.
In generale le temperature dei nodi allo stadio iniziale (corrispondente a t = 0) possono essere note a priori. Partendo da queste, sotto opportune condizioni al contorno, è possibile ricavare le temperature all’istante t = 1Dt (cioè t = 1). Analogamente le temperature dei nodi all’istante seguente si calcolano partendo da quelle dell’istante precedente.
Procedendo con questo metodo iterativo si viene a conoscenza delle temperature di tutti i nodi negli istanti considerati e si prosegue fino alla situazione stazionaria in cui più nulla cambia..
Per descrivere analiticamente il processo dobbiamo ricalcolare l’equazione di Fourier prendendo in considerazione il generico nodo n (e quindi la generica striscia DC) al generico istante e stimare le variazioni termodinamiche avvenute nell’intervallo di tempo Dt.
Dobbiamo quindi scrivere:
![]()
Considerando la lastra di spessore e altezza unitaria svolgiamo l’uguaglianza e otteniamo
![]()
dove QSN,IN è il calore che entra da sinistra e QDX,OUT è il calore che esce da destra.
Noto che ho inserito nel primo termine la differenza di temperatura del generico nodo n in due precisi istanti di tempo successivi. Questo è dovuto al fatto che il mio problema è impostato in forma finita e non più infinitesimale come eravamo abituati a considerare. Lo stesso discorso vale anche per il calore al secondo termine.
Calcoliamo ora i singoli termini
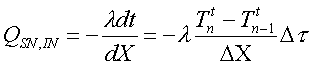
dove ho discretizzato la derivata attuando il rapporto incrementale.
Analogamente
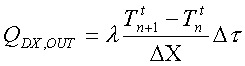
Ora sostituiamo
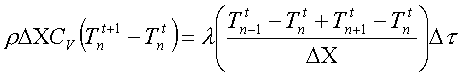
Ricordo che le temperature di tutti i nodi agli istanti t sono note e quindi la mia unica incognita è Tnt+1.
Ricaviamo quindi
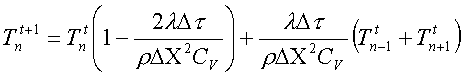
che è la formula risolutiva dei transitori.
Essa mi permette di ricavare i valori delle celle alla riga t+1 a patto che siano noti i valori della riga t.
Guardando questa formula osservo che non posso scegliere un Dt grande a piacere una volta che è stato fissato un passo spaziale DX. Potrebbe infatti succedere che il termine moltiplicativo di Tnt diventi negativo rendendo l’equazione numericamente instabile. Le temperature non tenderebbero così più al valore nominale effettivo, ma produrrebbero oscillazioni che andrebbero via via amplificandosi nel tempo mandando il computer in overflow.
Questo può essere logico anche intuitivamente in quanto non posso stimare un futuro troppo lontano se non conosco i passi intermedi, perché non ho abbastanza informazioni.
Questo è comunque un problema di tipo fisico che non posso risolvere cambiando semplicemente l’algorimo di calcolo.
Dobbiamo infatti ricordare che siamo giunti alla formula risolutiva partendo dal primo principio. Ipotizziamo di trovarci in una situazione in cui il nodo generico n ha una temperatura più bassa rispetto a quella dei nodi n-1 e n+1 che lo circondano e che il termine in esame sia negativo. Secondo la formula Tnt+1 dovrebbe quindi essere inferiore a Tnt. Questo però viola il secondo principio della termodinamica in quanto un corpo freddo circondato da due corpi più caldi si è trovato a cedere calore invece di riceverlo. Andiamo quindi incontro ad un paradosso.
Si può quindi introdurre il Dtlim che corrisponde al maggior passo temporale accettabile.
Imponendo la condizione di non negatività del termine sopra discusso:
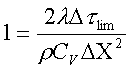
ricaviamo
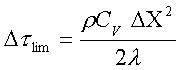
Bisogna però fare anche attenzione a non eccedere attuando una discretizzazione troppo fina. Infatti utilizzare passi troppo piccoli risulta essere dannoso per il processo di calcolo anche se teoricamente non sembrerebbe.
Visto che un eccesso di discretizzazione è altrettanto dannoso che una discretizzazione insufficiente si è vista la necessità di introdurre una discretizzazione ottima che garantisca il giusto compromesso tra le due.
Generalmente si usa utilizzare il seguente Dtott:
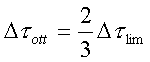
Se sostituiamo nell’equazione risolutiva il valore di Dtlim otteniamo
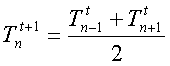
che corrisponde alla media temporale delle temperature del nodo n+1 e n-1 prese all’istante appena precedente.
Ogni cella risente quindi solo ed esclusivamente della presenza delle due celle che stanno, rispetto a lei, in alto a destra e in alto a sinistra.

Figura 3
- Schema risolutivo per un Dtlim.
Analogamente se usiamo Dtott otteniamo
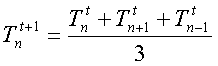
Quindi il valore della generica cella risulta essere calcolato come media delle tre celle che le stanno sopra.
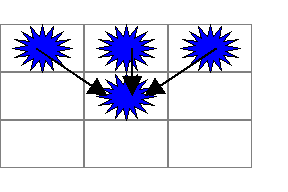
Figura 4 - Schema risolutivo per un Dtott.
ESEMPIO
Consideriamo una lastra di spessore S = 25 cm e diffusività a = (l/rC) = 0,023 m2/h. La temperatura della lastra è di 38 °C. Al tempo t = 0 Immergiamo il tutto in un pentolone d’olio bollente alla temperatura di 260 °C.
Vogliamo studiare il transitorio del materiale nei primi 3 minuti.
Prima di cominciare dobbiamo però specificare le condizioni al contorno, cioè il particolare comportamento della pelle della lastra. Ipotizziamo che la pelle (corrispondente alle coordinate X=0 e X=S) assuma, immediatamente con l’immersione, la temperatura dell’olio e che questa temperatura sia costante durante il transitorio.
Avremo quindi una temperatura della pelle Tp = 260 °C costante nei tre minuti.
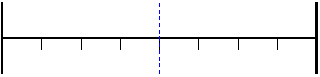
Possiamo quindi ora attuare la discretizzazione spaziale. Per semplicità discretizzo con 9 nodi (0,1,…8) e avremo quindi 8 divisioni.
Il passo spaziale risulta quindi essere:
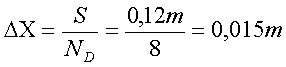
0
1 2 3 4 5
6 7 8
Figura 5
- Discretizzazione spaziale della lastra in
esame.
Dalla figura noto che il problema è simmetrico e quindi lo sarà anche la soluzione.
Possiamo perciò scrivere:
T0 = T8
T1 = T7
T2 = T6
T3 = T5
Decido di utilizzare il Dtlim da cui:
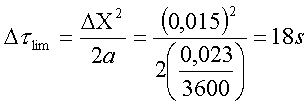
Per cui avremo (3*60/18)=10 passi temporali.
Possiamo ora cominciare a riempire la tabella con le temperature dei nodi ai vari istanti.
Io conosco a priori le condizioni al contorno e quelle iniziali. Per questo motivo sono immediatamente note la prima(e l’ultima) colonna e la prima riga.
Avremo cosi il nodo 1 e il nodo 8 costantemente alla temperatura di 260 °C. Analogamente al tempo t = 0 i nodi che non appartengono alla pelle avranno una temperatura di 38 °C.
Le temperature delle restanti celle si calcolano secondo la formula risolutiva trovata e discussa in precedenza. Per cui se vogliamo conoscere T11 ,cioè il valore della cella (1,1), dovremo fare la media aritmetica tra la cella (0,0) e la cella (2,0) per un valore numerico di (260+38)/2 = 149 °C.
Procedendo riga per riga iterativamente si viene a completare tutta la matrice e si conclude il problema.
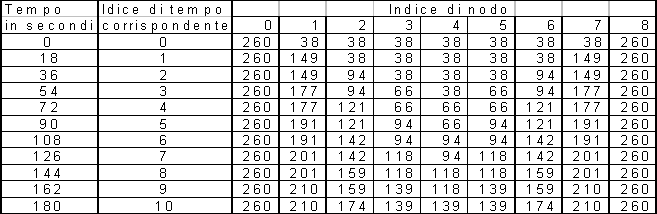
Figura
6 - Tabella risolutiva del
problema in esame usando il Dtlim.
Analizzando la tabella si può verificare la simmetria sopra descritta.
Si può anche notare che l’innalzamento progressivo delle temperature non è uguale per tutti i nodi, ma i nodi più esterni si scaldano più velocemente rispetto a quelli più interni.
Per descrivere più accuratamente questo fenomeno possiamo tracciare un grafico che descrive le temperature dei nodi in funzione dell’indice di tempo t.
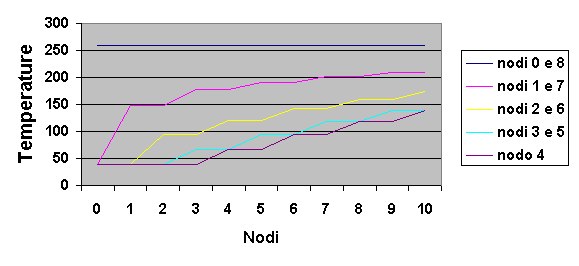
Figura 7
– Grafico che mostra la variazione della
temperatura in funzione dell’indice t per un Dtlim
Noto che le temperature di ciascun nodo non variano con continuità, ma per due istanti successivi assumono sempre lo stesso valore.
Questo problema è dovuto al fatto che noi calcoliamo il valore di ogni cella prendendo in considerazione solo le due celle che le stanno in alto a destra e in alto a sinistra
Se ripeto ora il calcolo utilizzando il Dtott = 2/3 Dtlim = 12 s devo considerare anche la temperatura dello stesso nodo all’istante precedente.
Da un lato quindi avrò un maggior numero di calcoli perché utilizzo un passo temporale più piccolo, ma dall’altro riesco ad ottenere un grafico che varia con continuità, a quindi più preciso.
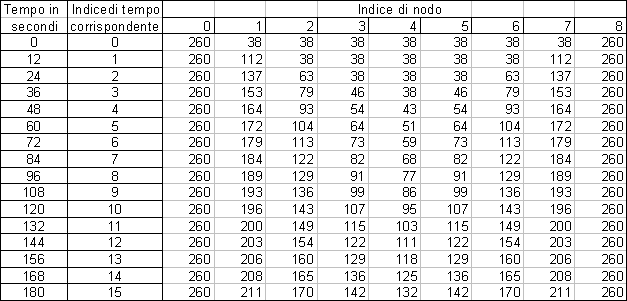 .
.
Figura 8
-
Tabella risolutiva del problema in esame usando un Dtott
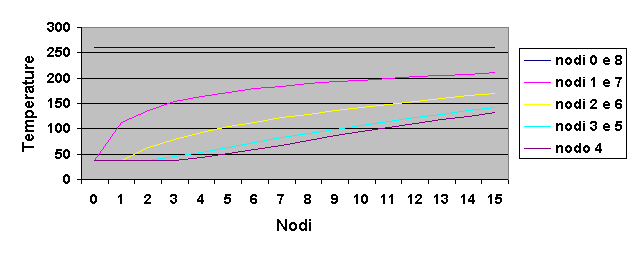
Figura 9
– Grafico che mostra l’andamento delle
temperature in funzione di t per un Dtott
Fino ad ora abbiamo considerato delle specifiche condizioni al contorno. Spesso invece succede che le temperature sulla pelle della lastra non siano bene precisate.
In particolare il primo nodo potrebbe essere connesso da una resistenza termica a una temperatura nota. Questa nuova condizione al contorno può ad esempio essere descritta da un certo coefficiente a dovuto alla convezione, all’irraggiamento o alla somma dei due.
Sotto queste nuove ipotesi devo andare ad analizzare il comportamento del primo nodo che è rappresentativo di una porzione di lastra pari a DC/2.
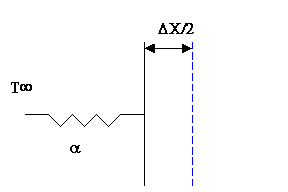
Figura 10
- Esempio di primo nodo connesso a una
temperatura nota tramite resistenza termica
Dato che non posso più ritenere costante la temperatura del primo e dell’ultimo nodo mi devo andare a calcolare anche per queste regioni una formula risolutiva.
Analogamente a quanto espresso in precedenza per i nodi interni avrò:
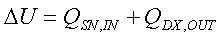
Per cui:
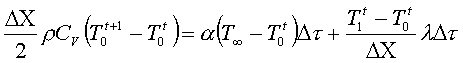
da cui si ricava
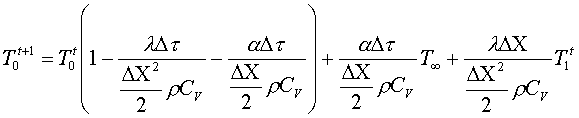
Questa è la formula ricorsiva che mi permette di calcolare la temperatura della pelle della lastra in funzione della temperatura che la stessa aveva all’istante precedente.
Anche in questo caso, guardando la formula, noto che il termine moltiplicativo di T0t potrebbe essere negativo provocando la violazione del secondo principio della termodinamica.. In particolare tanto più a è grande tanto più ci saranno problemi.
Dovrò quindi introdurre un passo per i nodi esterni, che difficilmente coincide con quello dei nodi interni, ma risulta essere più piccolo. Per risolvere questo inconveniente basta scegliere il più piccolo passo temporale e applicarlo su tutta la lastra (pelle compresa).
Possiamo quindi affermare a priori che la presenza di convezione mi porta ad usare passi temporali più piccoli.
Bisogna tener presente che in presenza da a molto grandi mi posso trovare davanti passi ridicolmente piccoli che mi portano a dover affrontare un’infinità di calcoli con grande dispendio di tempo e energia.
Uguagliando a zero il termine sopra descritto posso ricavate il massimo passo temporale applicabile sul primo nodo:
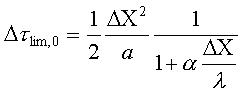
Possiamo a questo punto facilmente vedere la dipendenza del passo da a.
Guardando la formula possiamo notare anche la presenza del termine:
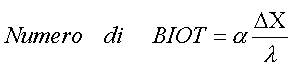
che rappresenta un numero puro ed è caratteristico dei fenomeni di transitorio termico.
Possiamo affermare che quando il numero di Biot >40 ,cioè con a molto grande, la temperatura alle pareti sia equivalente a quella all’infinito, e ricadiamo nel caso descritto in precedenza.
Viceversa se numero di Biot<0.1 si può ipotizzare che l’intera parete sia isoterma in ogni istante. In questo caso non avremmo un problema di transitorio in quanto la mia lastra entra subito istantaneamente a regime.
Nei casi intermedi la convezione e l’irraggiamento non sono trascurabili e devo studiare l’intero transitorio passo per passo anche sulle pelli.
Per risolvere problemi di questo genere devo utilizzare quello che è chiamato metodo implicito.
Fino ad ora abbiamo utilizzato un metodo esplicito in quanto era possibile esprimere un’unica incognita in funzione di termini tutti noti ragionando dal presente verso il futuro.
Il metodo implicito, viceversa, ragiona dal presente verso il passato.
Quando vado a fare il bilancio dell’energia avrò perciò una derivata temporale sinistra e non più destra.
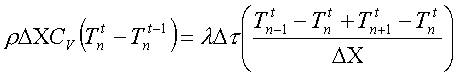
In questo caso però non posso ricavare subito la soluzione in quanto io conosco solo le temperature del passato. Ho quindi 3 incognite.
Noto però che io ho scritto il bilancio relativo solo al nodo generico n. Se io ripeto il calcolo per i nodi interni (n=1,…..n=n-1) alla fine trovo un sistema di n equazioni in n incognite risolvibile con tecniche di calcolo a noi note.
Una riga generica di questa matrice potrebbe essere
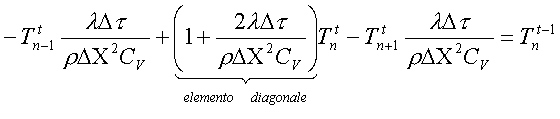
ripetendo lo stesso procedimento per tutti i nodi interni posso ottenere la seguente rappresentazione
![]()
dove A è una matrice tridiagonale.
Moltiplico entrambi i membri per A-1
![]()
Il vettore delle temperature cercate si ottiene quindi moltiplicando le temperature note per la matrice inversa di A.
Concludendo posso affermare che il metodo implicito è sempre stabile sotto qualsiasi condizione al contorno. Non ho più il problema di oscillazioni in caso di un passo temporale troppo ampio come succedeva utilizzando il metodo esplicito.