STRUMENTI PER LE MISURE IGROMETRICHE
Vi sono delle sostanze igroscopiche che possiedono la proprietà di assorbire l’umidità atmosferica. L’assorbimento di acqua da parte di tali sostanze ne altera le proprietà e questo fatto si può sfruttare per misurare, sia pure indirettamente, l’umidità relativa dell’aria. Infatti, quanto maggiore è l’umidità relativa tanto maggiore è la quantità d’acqua che le sostanze possono assorbire.
In questa sezione vengono presi in esame apparecchi capaci appunto di misurare l’umidità relativa di un gas o di un vapore, in particolare dell’aria atmosferica. Si possono distinguere:
1: Igrometro a capello
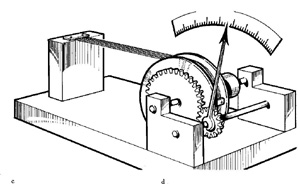
Contiene un fascetto di capelli (o peli animali), solitamente un misto di campioni di vario tipo, teso tra un punto fisso e uno mobile, tenuto da una molla. I capelli hanno la proprietà di accorciarsi all’aumentare del grado idrometrico. A seconda dell’umidità relativa dei capelli in esame, il punto mobile si sposta e muove, attraverso un sistema di ingranaggi e leve, una lancetta indicatrice. Questo strumento non si rivela molto preciso e soprattutto, per valori molto bassi dell’umidità, mostra una notevole inerzia.

Fig.1 – Igrometro a capello
Vi è una variante di questo strumento, chiamata igrografo, utilizzato nelle applicazioni di misura in campo meteorologico e in ambienti dove vi sono sistemi di trattamento aria che devono mantenere condizioni costanti (musei, biblioteche). E’ costituito da una cassetta metallica contenente una finestrella che permette l’entrata dell’umidità e da una parte trasparente in cui è situato un tamburo girevole avvolto da un rotolo di carta (occorre sostituirlo o ogni giorno o una volta a settimana), sul quale tre pennini lasciano traccia, movimentati, rispettivamente, da un termometro, un igrometro a capello e un barometro.
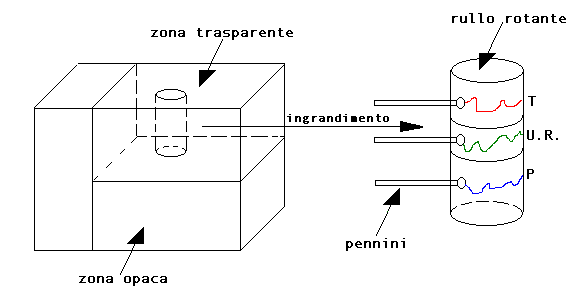
Fig.2 - Igrografo
2: Metodo della pesata
Normalmente impiegato in laboratorio, pesa l’effettivo quantitativo di umidità nell’aria, fornisce direttamente il titolo. Si compone di un tubo, contenente granuli di materiale avido d’acqua (H2SO4), da allacciare alla linea da analizzare e di un contatore volumetrico a scatti, in grado di determinare il volume d’aria in uscita.
Allacciando il tubo alla linea, il contatore comincerà a registrare i metri cubi d’aria secca uscenti dal dispositivo, in quanto l’aria umida in entrata avrà ceduto tutta l’acqua che contiene all’interno del tubo. Terminata l’acqusizione, si stacca il tubo, se ne misura il peso e lo si confronta col peso prima dell’operazione. Tale differenza è il peso dell’acqua catturata dal sale anidro. L’impiego in laboratorio sottintende una certa preparazione tecnica per riuscire ad utilizzare al meglio l’apparecchio.
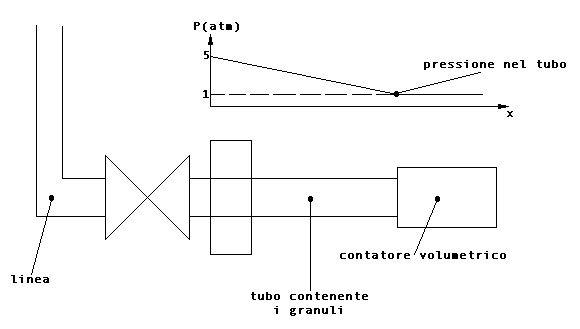
Fig.3 – Metodo della pesata
3: Igrometro a condensazione
Strumento attualmente in disuso. E’ costituito da un contenitore cilindrico di acciaio inox (a temperatura inferiore dell’ambiente) e da due termometri.
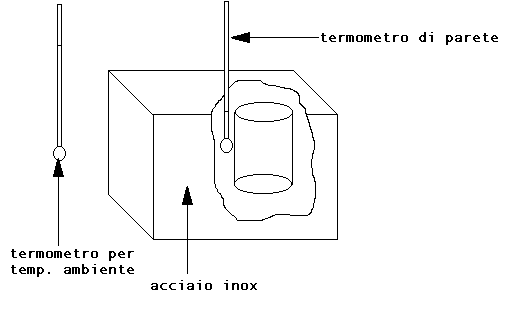
Fig.4 – Igrometro a condensazione
Il suo funzionamento è piuttosto semplice: dell’etere, fatto evaporare rapidamente per mezzo di una corrente d’aria, raffredda il recipiente di metallo che lo contiene e l’aria a contatto con la parete raggiunge una temperatura TB a cui corrisponde una certa pressione di vapore saturo; a questo punto un vapore umido si condensa e deposita sul metallo, rendendolo opaco. Con i due termometri si misurano le due temperature TA(ambiente) e TB(pozzo). E’ così possibile, mediante diagramma psicrometrico, ricavare il punto fisico di nostro interesse, e da esso ricavare i valori incogniti:
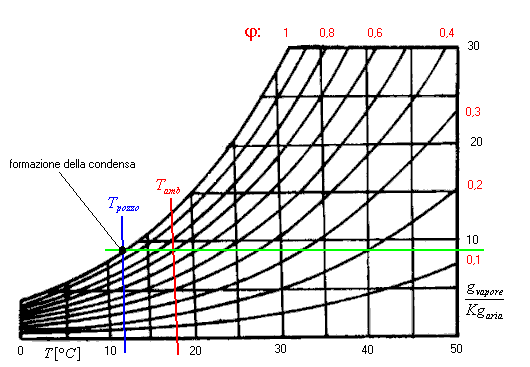
Fig.5 – Diagramma psicrometrico
Vi è anche la soluzione analitica, che sfrutta la seguente formula:
![]()
Le misurazioni fatte con questo strumento devono essere effettuate con grande prontezza, in quanto occorre leggere le temperature non appena si forma lo strato di condensa.
4: Igrometro elettronico
Contiene dispositivi che possono variare le loro caratteristiche elettriche in base a temperatura o umidità. In figura è realizzato un igrometro realizzato con un ponte di resistenze. Non appena la resistenza R2 varia, non ho più un insieme di quattro resistenze uguali, e la tensione misurata non è più nulla: è possibile stabilire una correlazione tra variazione di tensione e grado di umidità.
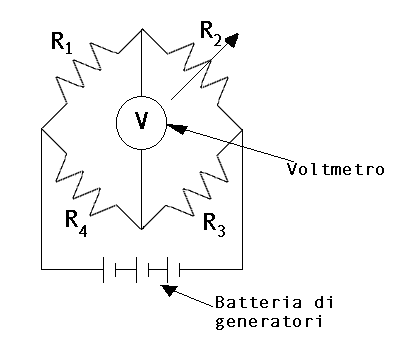
Fig.6 – Ponte di resistenze
Questo dispositivo ha una discreta precisione (1-2%) ed un costo piuttosto modesto rispetto ad altri strumenti di misurazione: viene ampiamente impiegato in ambito tecnico lavorativo ma limitatamente in laboratorio.
5: Fiale Drager
Questo strumento viene usato dai vigili del fuoco. E’ costituito da una pompa azionata a mano con molla di contrasto e da due terminali rigidi per l’aspirazione e la fuoriuscita dell’aria. Vi è inoltre una fiala di vetro da montare su uno dei due terminali, contenente dei granuli di materiale sensibile alla grandezza da analizzare. Una volta montata la fiala, si effettuano un numero di pompate indicate sulla fiala stessa al fine di farvi penetrare la sostanza di cui voglio conoscere la caratteristica; al termine dell’operazione una parte dei granuli in essa contenuti cambia colore: analizzandoli e leggendo la tacca indicante il livello del materiale , è possibile risalire direttamente alla grandezza in esame.
Non è un apparecchio precisissimo, tuttavia funziona a qualunque pressione; è robusto in quanto non possiede né parti elettroniche né parti meccaniche, vi si possono montare centinaia di fialette diverse e fare così analisi su varie caratteristiche fisiche di sostanze differenti. Occorre però tener presente che le fialette invecchiano con la luce e presentano una data di scadenza.
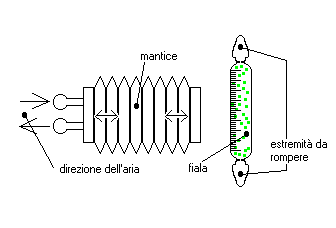
Fig. 7 – Fiala Drager con pompa a mano
6: Psicrometro (Igrometro di Assman)
E’ lo strumento più preciso in assoluto. Si compone di due termometri, uno detto a bulbo asciutto e l'altro detto a bulbo bagnato (il bulbo è il rigonfiamento posto nella parte inferiore del termometro, in cui è contenuto la maggior parte del mercurio).
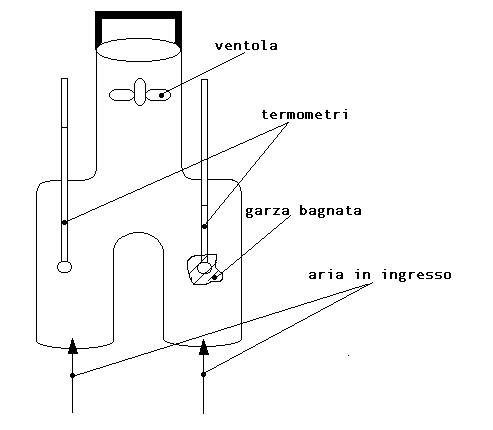
Fig.8 - Psicrometro
Il termometro a bulbo asciutto è un normale termometro. Quello a bulbo bagnato, invece, è così definito perchè il bulbo è avvolto da una garzina. L'operazione di lettura della temperatura di rugiada si chiama operazione psicrometrica e consiste nelle seguenti azioni: l'osservatore inumidisce la garzina con dell'acqua distillata (priva di impurità). Attraverso una ventolina, azionata o da una molla o da un motorino elettrico, viene forzata la ventilazione attorno al bulbo bagnato. Lo scopo della ventilazione forzata consiste nel sollecitare l'evaporazione dell'acqua di cui è imbevuta la garzina.
L'acqua comincia ad evaporare: questo processo comporta un consumo di energia che in questo caso si compie a spese del termometro, che pertanto si raffredderà: la colonnina di mercurio comincia a scendere fino a che il processo di evaporazione non termina.
A questo punto l'osservatore potrà leggere due valori di temperatura: uno sul termometro "asciutto" (TA), e l'altro sul termometro "bagnato"(TB). La temperatura di quest'ultimo ci fornirà il valore del punto di rugiada.
Attraverso il diagramma psicrometrico fornito a corredo dello strumento è possibile ricavare il valore dell'umidità relativa partendo dalle due temperature.
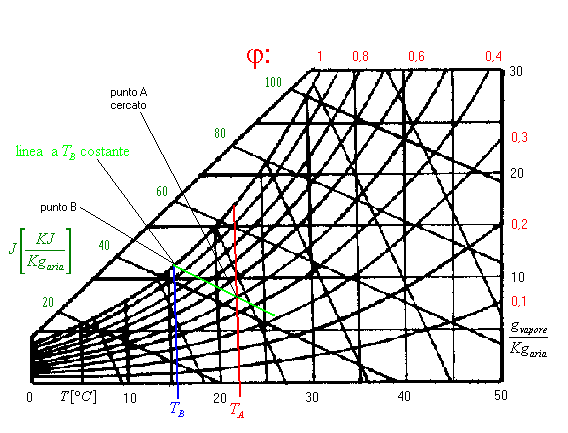
Fig.9 – Diagramma psicrometrico
Queste linee sono in prima approssimazione a entalpia J costante; in realtà le cose non sono propriamente così. Infatti sul sistema termometro+garza in un tempo infinitesimo dt si scambia un calore dQ da aria a garza; la temperatura di quest’ultima rimane fissa ed il calore fa evaporare una massa dM di acqua secondo la formula:
![]()
dove il meno sta ad indicare una diminuzione di massa.
La spiegazione fisica è semplice: l’aria ha abbassato la sua entalpia cedendo calore; considerando
![]()
uguagliando (2) e (3) ottengo:
![]()
dividendo entrambi i membri per dMa:
![]()
nelle quali è sottinteso essere x il titolo.
Ora cerco la pendenza della retta a entalpia J costante:
![]()
e sapendo che per il teorema del differenziale totale è:
![]()
applico la formula ed ottengo:
![]()
per una pendenza:
![]()
Confrontando le formule si nota facilmente che si ha lo stesso numeratore ma denominatori leggermente differenti; in prima approssimazione cioè le pendenze sono identiche.
Lo strumento esiste anche in una versione elettronica che sfrutta la termoresistenza PT100: consente una lettura immediata con una precisione ancora più elevata.
Esercizio 1: Scatolone adiabatico (sistemi aperti)
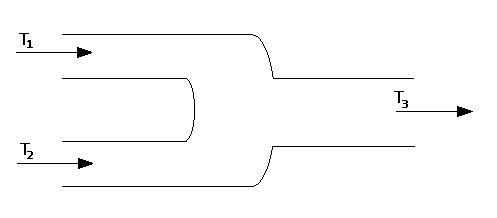
Forniti i seguenti dati in ingresso, determinare quelli d’uscita:
Portata in massa nel punto 1: MA1 = 400 Kgariasecca/h
Temperatura nel punto 1 : T1 = 32°C
Grado igrometrico in 1: j 1 = 0.8
Portata in massa nel punto 2: MA2 = 800 Kgariasecca/h
Temperatura nel punto 2 : T2 = 26°C
Grado igrometrico in 2: j 2 = 0.5
Portata in massa nel punto 1: MA3 = ?
Temperatura nel punto 1 : T3 = ?
Grado igrometrico in 1: j 3 = ?
Svolgimento:
Essendo lo scatolone adiabatico non ho scambi di calore con l’esterno, non verrà nemmeno compiuto su di esso alcuna forma di lavoro (Q=0, L=0). Inoltre, essendo in regime stazionario, non ho fenomeni di accumulo di massa e di energia, e posso quindi impiegarne le relative leggi di conservazione.
Per la massa vale:
![]()
Per cui ![]()
Troviamo ora i titoli di partenza in 1 e 2, usando la (11):
![]() (11)
(11)
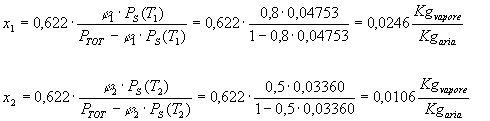
con i valori di PS(T1) = 0,04753 e PS(T2) = 0,03360 ottenuti mediante l’utilizzo della tabella in ultima pagina.
Se all’uscita l’umidità relativa j è minore di uno si conserva la portata in massa di vapore; ipotizzando che questo fatto sia vero, possiamo scrivere che:
![]() (12)
(12)
Da cui:
![]()
Per l’energia ho invece (trascurando le variazioni di energia potenziale e cinetica):
![]()
Effettuo quindi il calcolo:
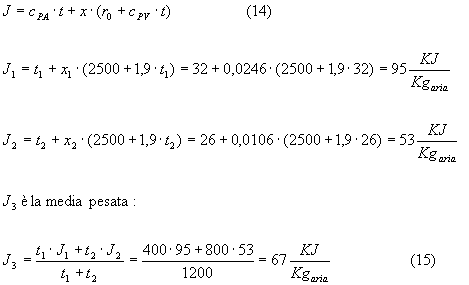
Per ricavare la temperatura in 3 utilizzo ancora la (14):
![]()
Per ottenere il grado igrometrico utilizzo la tabella, conoscendo T3:
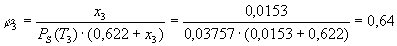
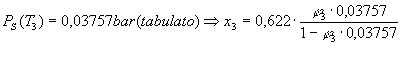
risultato che giustifica ampiamente l’ipotesi della conservazione della portata in massa di vapore.
Risolvendo il problema per via grafica (fig.10), il risultato di T3(28°C), risulta abbastanza prossimo a quello trovato in precedenza. Esso si troverà su di un punto del diagramma psicrometrico, contenuto nel segmento congiungente gli estremi pari ai valori corrispondenti di T1 e T2:
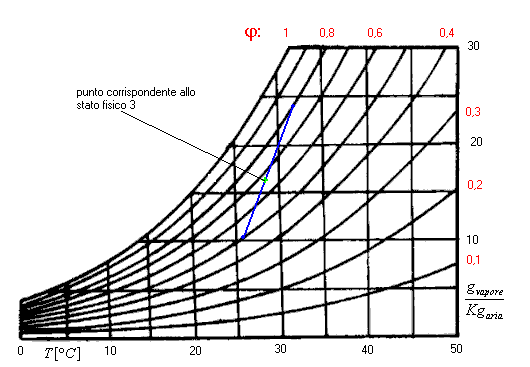
Fig.10 - soluzione grafica del problema
Supponendo una miscelazione con due masse aventi grado igrometrico prossimo all’unità, si sarebbe potuto ottenere il punto relativo allo stato fisico finale sulla curva a j=1 (stato della nebbia), corrispondente a una miscela bifasica fatta di goccioline; se addirittura viene superata tale curva si ha la condizione della pioggia che si verifica quando aria calda e umida si miscela con aria fredda e umida (fig.11).
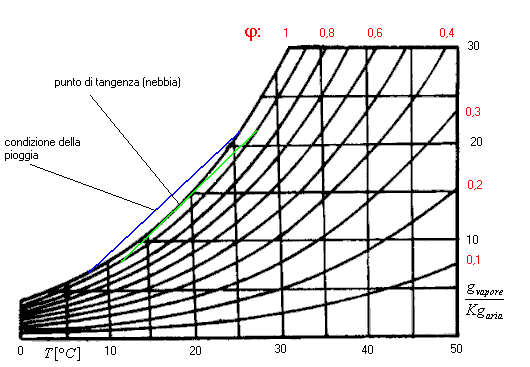
Fig.11 – caso della nebbia e della pioggia
Esercizio 2: Condizionatore d’aria
Funzionamento:
Il condizionatore in figura preleva aria alla temperatura T1 attraverso la bocchetta A, mediante la ventola B. In seguito, all’aria aspirata viene tolto calore tramite la batteria alettata C (un insieme di lamierini d’alluminio che lasciano passare l’aria). L’aria raggiunge così la temperatura incognita T2. Una parte di vapore in esso contenuta condensa e l’acqua che precipita viene raccolta da una serie di lamierini zigrinati (sezione D in figura) e fatta defluire attraverso il canale di scolo F. L’aria trattata, prima di essere espulsa, viene in seguito fatta passare attraverso una seconda batteria alettata E, che la riscalda, onde evitare l’emissione di aria satura fredda nell’ambiente.
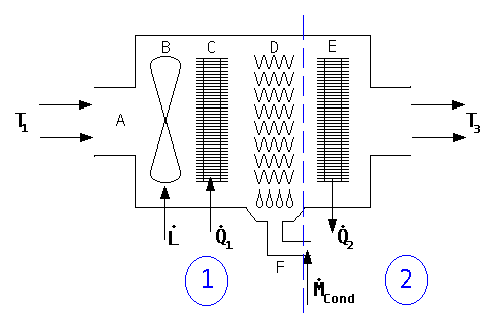
Fig.12 – Condizionatore d’aria
Il condizionatore viene montato in un’aula di 470 m3, e si richiede che l’ambiente sia sottoposto a un ricambio orario, cioè che ad ogni ora venga ricambiato un volume d’aria pari al volume dell’ambiente stesso. Tutto il processo avviene a pressione costante.
Pressione: Ptot = 1 bar
Temperatura aria esterna: T1 = 32°C
Grado igrometrico aria esterna: j 1 = 0,8
Temperatura aria trattata: T3= 20°C
Grado igrometrico aria trattata: j 3 = 0,5
Potenza ventola: L = 450 W
Volume ambiente: V = 470 m3
Temperatura aria dopo raffreddamento: T2 = ?
Portata tubo di scolo: Mcond = ?
Potenza assorbita batteria C: Q1 = ?
Potenza fornita batteria E: Q2 = ?
Svolgimento:
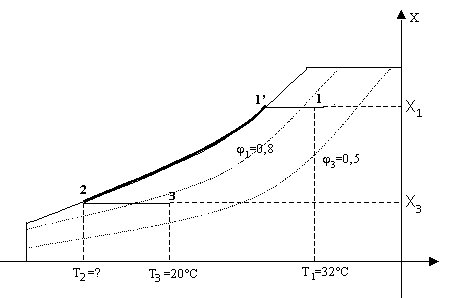
Fig.13 – Diagramma psicrometrico del processo
1à1’: l’aria entra ad una temperatura di 32°C e viene raffreddata (il titolo rimane costante) dalla batteria C fino a quando non comincia a condensare il vapore;
1’à2: una quantità sempre maggiore di vapore si condensa e l’aria continua a raffreddarsi: il titolo della miscela di conseguenza si abbassa finchè viene raggiunta la temperatura incognita T2;
2à3: l’aria viene infine postriscaldata dalla batteria E, mantenendo ovviamente il titolo costante, fino a raggiungere la temperatura T3 di 20°C.
E’ possibile ricavare i titoli x1 e x3 dell’aria in ingresso e in uscita dal condizionatore, mediante l’utilizzo congiunto della (22) e della tabella in ultima pagina, grazie alla quale è possibile ricavare PS tenendo presente che nei punti 1 e 3 la temperatura vale rispettivamente 32°C e 20°C.
![]() (16)
(16)
Sostituendo i valori numerici si ottiene:
![]()
![]()
per ricavare la portata in massa di condensato è sufficiente moltiplicare la portata in massa dell’aria trattata con la differenza dei 2 titoli appena ricavati:
![]() (17)
(17)
I dati del problema, però, danno solo informazioni relative alla portata in volume dell’aria da trattare, non in massa. Per ricavare una portata dall’altra è necessario considerare l’aria secca come un gas perfetto ed applicare la relativa equazione di stato:
![]() (18)
(18)
Viene assunta come temperatura T il valore T3 di 20°C, in quanto la portata volumetrica che il condizionatore deve sopportare è relativa all’aria che esce a 20°C, non a quella che entra dall’esterno a 32°C. E’ ancora ignota la pressione parziale dell’aria secca pA3. Per ricavarla, si utilizza la legge di Dalton:
![]() (19)
(19)
da cui, considerando ptot pari alla pressione atmosferica di 1 bar, e sfruttando la definizione di grado igrometrico j, si ricava:
![]()
Sostituendo infine i valori numerici, la pressione parziale dell’aria secca risulta essere
![]()
Sostituendo i valori numerici nella (18) si ottiene
![]()
dove:
![]() (19)
(19)
in cui mA rappresenta la massa molare dell’aria secca, considerata pari a 29kg/mol, mentre R0 è espressa in unità del S.I. Per ottenere una portata in chilogrammi orari, (essendo 470 il valore di metri cubi orari), il valore di pA3 è stato espresso in chilopascal.
A questo punto è possibile sostituire i valori numerici nella (17)
![]()
Ora, per calcolare la temperatura T2 dell’aria all’uscita dalla batteria alettata C, utilizzo ancora la (16) e calcolo pS2, pressione parziale del vapore di saturazione nel punto 2, vista l’uguaglianza tra x2 e x3. Considero stavolta il valore di j unitario, dal momento che il punto 2 si trova sulla curva limite del diagramma psicrometrico. Sostituendo i valori già ricavati si ottiene:
![]()
Utilizzando ancora la Tabella si ricava, interpolando, che T2=9,5°C.
Non rimangono che da determinare le potenze assorbite e cedute rispettivamente dalle batterie alettate C ed E. Posso considerare il mio condizionatore come l’unione di due sottosistemi aperti (vedi fig.12). Considero il sottosistema 1 (aria entra a 32 °C ed esce a 9,5C°) e ne scrivo il seguente bilancio energetico, considerando come convenzione, positive le entalpie uscenti dal sistema e negative quelle entranti.:
![]() (20)
(20)
dove con J1 e J2 indico le entalpie specifiche dell’aria nei punti 1 (aria entrante) e 2 (aria uscente), ricavate dalla formula :
![]() (21)
(21)
Sostituendo in (21) ottengo:
![]()
![]()
L’entalpia hliq che appare nella (20) è relativa alla massa di acqua che condensa contro i lamierini zigrinati (sezione D), la quale si calcola con la seguente formula:
![]() (22)
(22)
in cui il calore specifico CL ha, come noto per l’acqua, il valore di 4,187 kJ/kg°K, mentre Tcond rappresenta la temperatura dei lamierini zigrinati. Questa temperatura, tuttavia non è uguale a quella dell’aria in questa sezione, cioè 9,5°C, poiché la batteria di lamierini, essendo bagnata (l’acqua vi condensa contro), sicuramente si troverà ad una temperatura leggermente inferiore a quella dell’aria da cui è attraversata. Approssimativamente si può considerare la temperatura Tcond pari a 8°C. Sostituendo nella (22) i valori numerici indicati, si ottiene
![]()
Infine, il termine![]() , che rappresenta la potenza fornita dalla
ventola, è pari (vedi dati del problema) a –0,45kW in
quanto la potenza è entrante nel sistema. Sostituendo nella (27)
i valori numerici, ed esplicitando rispetto a Q1,
si ottiene:
, che rappresenta la potenza fornita dalla
ventola, è pari (vedi dati del problema) a –0,45kW in
quanto la potenza è entrante nel sistema. Sostituendo nella (27)
i valori numerici, ed esplicitando rispetto a Q1,
si ottiene:
![]()
Da notare che il termine 1/3600 è stato introdotto per trasformare le portate in massa da chilogrammi all’ora in portate al secondo, in modo da ottenere il risultato in chilowatt.
Passando al sottosistema 2, occorre effettuare il bilancio energetico considerando l’aria entrante ad una temperatura di 9,5°C e quella uscente ad una temperatura di 20°C per effetto del calore rilasciato dalla batteria:
![]() (23)
(23)
In questo caso non entra energia dall’esterno e non si hanno perdite di massa per condensazione. L’unico termine ancora ignoto è J3, il quale viene calcolato tramite la (21), considerando una temperatura di 20°C, cioè quella dell’aria in uscita.
![]()
Sostituendo i relativi valori nella (23) si ottiene il valore cercato
![]()
Tabella utilizzata nella risoluzione degli esercizi:
| Temperatura
aria T (°C) |
Pressione di vapore dell’aria satura P (mbar) P (mmHg) |
Titolo
di saturazione x g/Kg |
|
-20 |
1.02 |
0.756 |
0.63 |
-18 |
1.25 |
0.938 |
0.77 |
-16 |
1.5 |
1.125 |
0.93 |
-14 |
1.81 |
1.358 |
1.11 |
-12 |
2.17 |
1.628 |
1.34 |
-10 |
2.59 |
1.943 |
1.6 |
-8 |
3.09 |
2.318 |
1.91 |
-6 |
3.67 |
2.753 |
2.27 |
-4 |
4.36 |
3.270 |
2.69 |
-2 |
5.16 |
3.870 |
3.19 |
0 |
6.09 |
4.568 |
3.78 |
1 |
6.56 |
4.920 |
4.07 |
2 |
7.04 |
5.280 |
4.37 |
3 |
7.57 |
5.678 |
4.7 |
4 |
8.11 |
6.083 |
5.03 |
5 |
8.7 |
6.526 |
5.4 |
6 |
9.32 |
6.991 |
5.79 |
7 |
9.99 |
7.493 |
6.21 |
8 |
10.7 |
8.026 |
6.65 |
9 |
11.46 |
8.596 |
7.13 |
10 |
12.25 |
9.188 |
7.63 |
11 |
13.09 |
9.818 |
8.15 |
12 |
13.99 |
10.493 |
8.75 |
13 |
14.94 |
11.206 |
9.35 |
14 |
15.95 |
11.963 |
9.97 |
15 |
17.01 |
12.759 |
10.6 |
16 |
18.13 |
13.599 |
11.4 |
17 |
19.32 |
14.491 |
12.2 |
18 |
20.59 |
15.444 |
12.9 |
19 |
21.92 |
16.441 |
13.8 |
20 |
23.31 |
17.484 |
14.7 |
21 |
24.8 |
18.602 |
15.6 |
22 |
26.37 |
19.779 |
16.6 |
23 |
28.02 |
21.017 |
17.7 |
24 |
29.77 |
22.3 |
18.8 |
25 |
31.6 |
23.702 |
20 |
26 |
33.53 |
25.150 |
21.4 |
27 |
35.56 |
26.672 |
22.6 |
28 |
37.71 |
28.285 |
24 |
29 |
39.95 |
29.965 |
25.6 |
30 |
42.32 |
31.748 |
27.2 |
31 |
44.82 |
33.618 |
28.8 |
32 |
47.46 |
35.575 |
30.6 |
33 |
50.18 |
37.638 |
32.5 |
34 |
53.07 |
39.806 |
34.4 |
35 |
56.1 |
42.078 |
36.6 |
36 |
59.26 |
44.449 |
38.8 |
37 |
62.6 |
46.954 |
41.1 |
38 |
66.09 |
49.572 |
43.5 |
39 |
69.75 |
51.317 |
46 |
40 |
73.58 |
55.198 |
48.8 |
41 |
77.59 |
58.197 |
51.7 |
42 |
81.8 |
61.355 |
54.8 |
43 |
86.18 |
64.64 |
58 |
44 |
90.79 |
68.098 |
61.3 |
45 |
95.6 |
71.706 |
65 |
46 |
100.61 |
75.464 |
68.9 |
47 |
105.87 |
79.409 |
72.8 |
48 |
111.33 |
83.504 |
77 |
49 |
117.07 |
87.81 |
81.5 |
50 |
123.04 |
92.288 |
86.2 |
55 |
150.94 |
117.715 |
114 |
60 |
198.7 |
149.037 |
152 |