Equazione di bilancio di massa
Valutiamo la massa del sistema
aperto al tempo 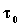 , troviamo:
, troviamo:
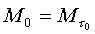 (2)
(2)
Successivamente, trascorso il tempo Dt , misureremo al tempo t+Dt una
massa pari a :
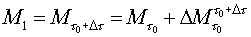 (3)
(3)
Per affrontare lo studio di un sistema aperto ci serviremo
anche di un sistema chiuso ausiliario a massa costante definito in maniera tale
da comprendere (all’istante iniziale 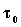 ) tutta la massa contenuta nel sistema aperto ed in più una
porzione di massa
) tutta la massa contenuta nel sistema aperto ed in più una
porzione di massa 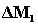 collocata
immediatamente a monte della sezione 1 d’ingresso del fluido.
collocata
immediatamente a monte della sezione 1 d’ingresso del fluido.
confine sistema chiuso
 confine sistema
aperto
confine sistema
aperto
Fig.
2: sistema aperto e corrispondente sistema chiuso ausiliario agli istanti: a)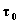 ; b)
; b) 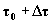 .
.
Nel
sistema chiuso ausiliario troviamo al tempo 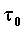 una massa di:
una massa di:
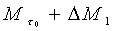 (4)
(4)
a al
tempo 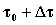 una massa di:
una massa di:
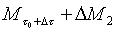 (5)
(5)
Solitamente
si ha che:
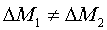 (6)
(6)
questa disuguaglianza diviene però un’uguaglianza se ci
troviamo a studiare un sistema in regime permanente, cioè un sistema in cui
entra una quantità di massa pari a quella che esce.
Considerando il sistema chiuso, che è a massa
costante per definizione, possiamo uguagliare la (4) e la (5):
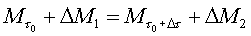 (7)
(7)
Dividendo termine a termine per 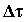 :
:
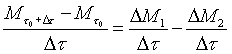 (8)
(8)
Dalla definizione di derivata al
tendere di Dt a zero abbiamo:
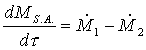 (9)
(9)
Avendo definito: 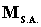 la massa del sistema
aperto e le portate in massa
la massa del sistema
aperto e le portate in massa 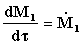 ,
, 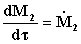 , ed avendo considerato
positive le portate in massa entranti nel sistema e negative quelle uscenti.
, ed avendo considerato
positive le portate in massa entranti nel sistema e negative quelle uscenti.
In generale, se la massa entra ed
esce da più sezioni abbiamo:
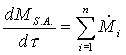 (10)
(10)
Se oltre a poter trascurare gli effetti
relativistici, siamo anche in presenza di m componenti che non reagiscono fra
loro, l’equazione (10) degenera in m equazioni; in questo caso bisogna
specificare che abbiamo m equazioni indipendenti e non m+1, perché una è
esprimibile tramite le rimanenti m.
Equazione di bilancio dell’energia
Per arrivare a scrivere un’equazione di bilancio
dell’energia indichiamo convenzionalmente positivo il lavoro fatto dal sistema
sull’ambiente, e positivo il calore fornito dall’ambiente al sistema.
Solitamente il lavoro scambiato fra sistema aperto ed ambiente è dato dalla
rotazione di un albero dovuta al passaggio del fluido, se è il sistema a
compiere lavoro, o ad un motore se è l’ambiente a compiere lavoro.
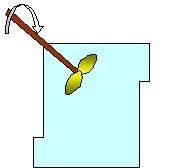
Fig.
3: schematizzazione del lavoro scambiato fra sistema ed ambiente.
Valutiamo
l’energia all’istante iniziale e all’istante finale, considerando anche forme
d’energia come quella potenziale e cinetica che erano state supposte
trascurabili per i sistemi chiusi.
Indicando
con 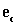 ,
, 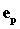 ,
,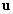 , rispettivamente le energie specifiche cinetica, potenziale
ed interna abbiamo che all’istante
, rispettivamente le energie specifiche cinetica, potenziale
ed interna abbiamo che all’istante 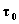 la massa
la massa 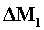 contiene un’energia
pari a :
contiene un’energia
pari a :
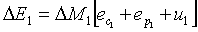 (11)
(11)
la massa 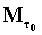 un’energia:
un’energia: 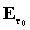 .
.
All’istante
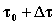 la massa
la massa 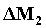 ha un’energia:
ha un’energia:
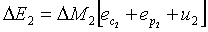 (12)
(12)
la massa 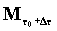 un’energia:
un’energia: 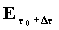 .
.
Solitamente non sono specificate
le energie contenute in 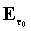 ed in
ed in 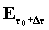 perché non ci
interessa sapere che tipo di energie siano.
perché non ci
interessa sapere che tipo di energie siano.
Dobbiamo
relazionare in funzione della variabile temporale anche i flussi di lavoro e di
calore, per cui abbiamo che il lavoro ed il calore scambiati in Dt
saranno rispettivamente:
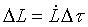 (13)
(13)
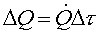 (14)
(14)
ove si è
indicato con 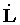 la potenza meccanica
e con
la potenza meccanica
e con 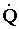 la potenza termica.
la potenza termica.
Ora ci manca da calcolare il lavoro di “pompaggio”
del fluido in entrata ed in uscita, perché in effetti il sistema chiuso si è
deformato nel lasso di tempo trascorso fra l’istante iniziale e l’istante
finale della nostra osservazione.
Allora
poiché:
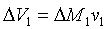 (15)
(15)
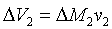 (16)
(16)
e poiché l’equazione di bilancio di energia per un sistema
chiuso afferma:
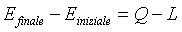 (17)
(17)
si ha:
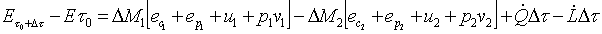 (18)
(18)
Nella sovrastante equazione si è
tenuto conto che  è data dalla somma
dell’energia contenuta nella massa
è data dalla somma
dell’energia contenuta nella massa 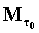 e
e 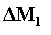 più il lavoro di “pompaggio” del fluido verso l’interno del
sistema aperto ed
più il lavoro di “pompaggio” del fluido verso l’interno del
sistema aperto ed 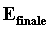 è la somma
dell’energia contenuta in
è la somma
dell’energia contenuta in 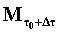 e
e 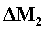 più il lavoro di “pompaggio” verso l’esterno; inoltre si è
sostituito ad
più il lavoro di “pompaggio” verso l’esterno; inoltre si è
sostituito ad 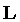 e
e 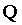 rispettivamente
l’equazione (13) e (14).
rispettivamente
l’equazione (13) e (14).
Ora ricordando che:

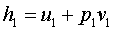 (19)
(19)
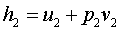 (20)
(20)
sostituendo la (19) e la (20)
nell’equazione (18) e dividendo termine a termine per 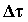 otteniamo:
otteniamo:
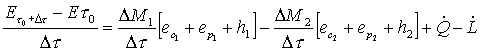 (21)
(21)
facendo tendere 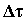 a zero:
a zero:
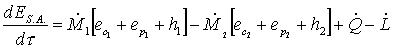 (22)
(22)
ove 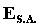 indica l’energia del sistema aperto.
indica l’energia del sistema aperto.
Se ci troviamo nella situazione di regime
permanente:
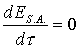 (23)
(23)
quindi l’energia del sistema aperto è costante; inoltre in
questa particolare condizione:
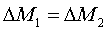 (24)
(24)
Cioè vale:
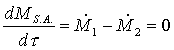
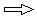
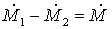 (25)
(25)
l’equazione di bilancio
dell’energia in regime permanente risulta quindi essere:
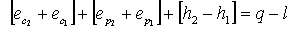 (26)
(26)
ove: 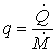 ;
; 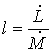
Si noti che tutti i termini dell’equazione (26)
sono energie specifiche pertanto misurabili in J/kg.
Generalmente si incontrano delle difficoltà nel
calcolare l’energia potenziale e quella cinetica perché di solito non sono
costanti lungo la sezione del sistema salvo che in casi particolarmente
semplici, mentre per l’entalpia resta valido il metodo usato per calcolarla
attraverso le tabelle.
Per un corpo rigido vale:
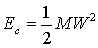 (27)
(27)
ma un fluido non è un corpo
rigido in movimento, per cui si definisce la velocità media W come quel valore ipotetico della
velocità parallelo all’asse del condotto che, uniforme su tutta la sezione
normale S sarebbe in grado di dare
la stessa portata in volume che si ha nella realtà.
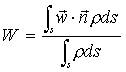 (28)
(28)
Se la densità r
è costante:
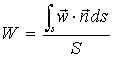 (29)
(29)
Inoltre abbiamo che:
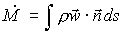 (30)
(30)
Con r costante:
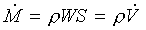 (31)
(31)
ove 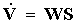 è la portata in volume.
è la portata in volume.
Quindi:
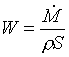 (32)
(32)
La velocità media è però
un cattivo indicatore per l’energia cinetica poiché scrivendo
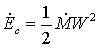 (33)
(33)
non
teniamo conto dei contributi dovuti alle componenti della velocità fuori asse
che si presentano nei liquidi con moti vorticosi e del fatto che il quadrato del
valore medio è minore del valore medio dei quadrati.
Per questo motivo si
introduce un coefficiente correttivo a>1 per cui:
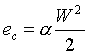 (34)
(34)
Il coefficiente a è
di difficile determinazione, fatta eccezione per alcune particolari situazioni:
·
se siamo in presenza di un fluido avente un profilo di
velocità parabolico di Poiseville, si riscontra: a=2. Tale valore di a
è ritenuto un tetto superiore perché è molto difficile ottenere un moto
laminare di Poiseville;
·
se abbiamo un moto rigido, ove cioè un piccolo strato
di fluido sul bordo della conduttura ha moto relativo ed il corpo centrale del
fluido si muove rigidamente, allora: a=1;
·
se abbiamo un
moto fortemente turbolento ove la velocità media è pressoché costante a causa
della viscosità del fluido allora si trova: a=1.
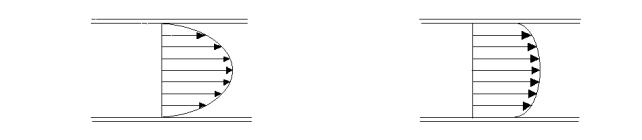
a)
b)
Fig. 4: profili di velocità per fluido in moto : a)
laminare; b) turbolento
Possiamo quindi esprimere
l’energia cinetica specifica come:
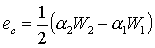 (35)
(35)
L’energia potenziale di un
corpo si esprime:
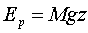
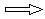
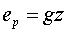 (36)
(36)
Poiché si pone per
semplicità nell’equazione (35) 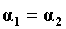 , possiamo scrivere l’equazione di bilancio dell’energia
nella seguente forma:
, possiamo scrivere l’equazione di bilancio dell’energia
nella seguente forma:
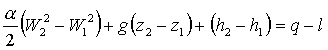 (37)
(37)
Se l’energia cinetica e
quella potenziale sono trascurabili, allora la (37) diviene:
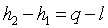 (38)
(38)
CICLO DI RANKINE
Poiché la massima produzione di lavoro a parità di calore
fornito si ha per la macchina di Carnot che è però una macchina non fisicamente
realizzabile, si è cercato di trovare una soluzione pratica a questo problema e
si è visto che la macchina di Rankine bene approssima il rendimento di quella
di ideale di Carnot.
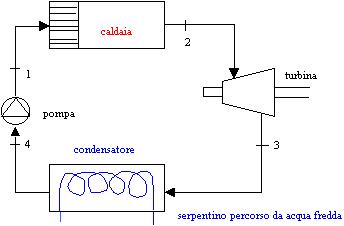
Fig. 5: schema della
macchina di Rankine
La macchina di Rankine è una macchina a vapore utilizzata su
ampia scala, soprattutto per produrre energia elettrica nelle centrali
termoelettriche.
Solitamente all’interno di queste macchine si usa dell’acqua
demineralizzata a pH neutro, perciò è importante riuscire a recuperarla per il
suo costo elevato; essa verrà pertanto rimpiazzata solo per le frazioni perse
negli sfiati e nelle valvole.
Il ciclo di Rankine si presta bene ad essere studiato
attraverso la matematica dei sistemi aperti.
All’interno della turbina il gas si espande compiendo lavoro
e mettendo in rotazione il rotore della stessa.

Fig. 6: disegno di una turbina a vapore con spaccato che rende visibili
sia lo statore che il rotore.

Fig.
7: sezione di una turbina in fase di montaggio, si notano le “alette” del
rotore.
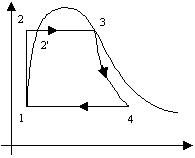
Osserviamo il diagramma pv del ciclo di Rankine:
p
 v
v
Fig.
8: diagramma del ciclo di Rankine.
Descriviamo il ciclo punto per punto:
da 1 a 2: il
fluido che è nella fase liquida viene compresso mediante la pompa;
da 2 a 2’ e
da 2’ a 3: il fluido viene riscaldato e poi vaporizzato a pressione costante per
mezzo di una caldaia;
da 3 a 4: il
fluido nella fase di vapore saturo secco compie lavoro espandendosi
isoentropicamente nella
turbina;
da 4 a 1: il
fluido ora nella fase di vapore saturo a bassa pressione viene condensato nella
fase
liquida a pressione e temperatura
costanti per mezzo di un condensatore all’interno del
quale si trova un serpentino
percorso da acqua fredda.

![]() (1)
(1)
![]()
![]()

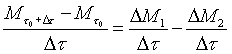
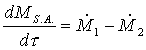
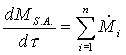

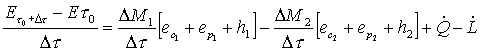
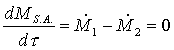
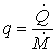
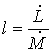
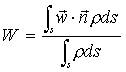
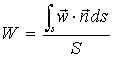
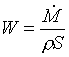
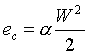
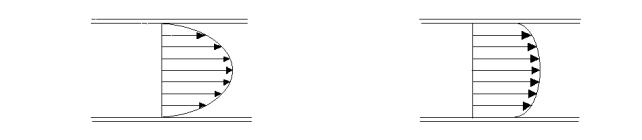
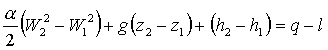



 v
v