Onde Sferiche
La trattazione fino ad ora eseguita,riguardo lo studio delle onde acustiche,è stata incentrata sul comportamento delle onde piane,cioè di quelle particolari manifestazioni oscillatorie riguardanti l’aria, che si manifestano all’interno di cilindri (nell’idealità di lunghezza infinita) come possono essere,ad esempio,le canne di un organo o i condotti di aspirazione e scarico di un motore a combustione interna.
Anche dall’inattuabilità pratica della ‘ipotesi pistone infinito’ ,nasce l’esigenza di considerare in termini per quanto possibili rigorosi,la situazione di onde che si propagano nello spazio tridimensionale,come accade,in effetti,per onde in uscita da un cilindro di lunghezza finita,o più semplicemente per quelle onde che vengono emesse da un comunissimo altoparlante.
Focalizzeremo la nostra attenzione sulla cosiddetta sorgente sonora sferica,la cui principale caratteristica è quella che tutti i punti della sua superficie vibrano uniformemente in fase spostandosi radialmente rispetto alla posizione di equilibrio per effetto di contrazioni ed espansioni;le onde generate da una simile sorgente,dette appunto onde sferiche,si propagano allora con le stesse modalità in tutte le direzioni,mantenendo sempre la simmetria sferica,per cui il fronte d’onda sarà costituito da superfici sferiche concentriche (Fig.1).
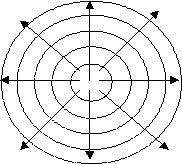
Figura 1
Nello studio di questa nuova situazione la particolare geometria del problema,impone ,come è logico pensare,l’utilizzo di coordinate sferiche e cilindriche,qui sotto brevemente richiamate:
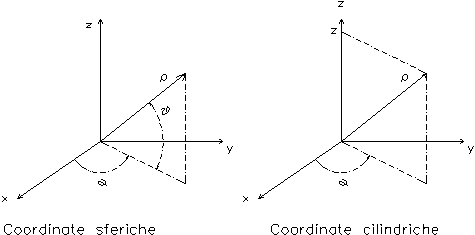
Figura 2
Coordinate sferiche: Coordinate cilindriche:
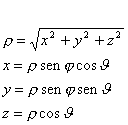
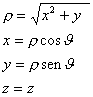
Fatte queste premesse è allora possibile scrivere l’equazione di D’Alambert in coordinate sferiche:
![]() (1)
(1)
dove:

La soluzione di questa equazione differenziale,necessita
dell’imposizione di una condizione al contorno,che in questo caso viene
rappresentata dalla velocità delle particelle d’aria che si misura sulla
superficie della sorgente sonora sferica;indicando il raggio di tale sfera con ![]() ,mi pongo nella condizione
,mi pongo nella condizione ![]() e la velocità in tale
condizione è:
e la velocità in tale
condizione è:
![]() (2)
(2)
E’ bene sottolineare come questa condizione al contorno sia congruente con l’ipotesi di aderenza delle particelle d’aria nelle vicinanze della superficie sferica.
La soluzione cercata è,dunque, del tipo:
![]() (3)
(3)
dove K è il numero d’onda (![]() ) e
) e ![]() è una costante da definire,imponendo alla 3 la
condizione 2;in effetti la generica velocità u,altro non è che la derivata
spaziale del potenziale di velocità,per cui:
è una costante da definire,imponendo alla 3 la
condizione 2;in effetti la generica velocità u,altro non è che la derivata
spaziale del potenziale di velocità,per cui:
![]() (4)
(4)
che nella condizione r=![]() ,deve essere uguale alla 2:
,deve essere uguale alla 2:
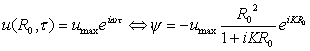
(5)
Ciò significa,in definitiva, che posso scrivere la generica velocità u come:
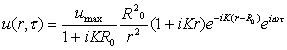 (6)
(6)
Mentre per
quel che riguarda la pressione ho:
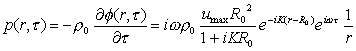 (7)
(7)
La 6 e la 7 permettono,infine di calcolare l’impedenza Z:
![]() (8)
(8)
Oppure,poichè K=![]() :
:
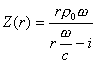 (9)
(9)
Occorre allora notare alcune cose fondamentali:
L’impedenza è una grandezza complessa caratterizzata da un modulo e da una fase;
L’impedenza è il rapporto di due grandezze complesse sfasate tra di loro:ciò implica un trasporto di energia non ottimale in quanto il maggior rendimento possibile si avrebbe con le due grandezze in fase.
L’impedenza dipende dalla distanza r a cui mi pongo rispetto alla sorgente sonora.
A questo proposito,è interessante osservare come varia la
funzione Z(r) nei casi estremi di distanza r molto piccola e molto grande
rispetto alla lunghezza d’onda ![]() .
.
Cominciamo con ![]() :
:
![]() (10)
(10)
Mentre se ![]() trovo:
trovo:
![]() (11)
(11)
E’ allora notevole sottolineare che se r>>![]() ,l’impedenza assume valore puramente reale e la sua fase è
ovviamente nulla:ci si ritrova,pertanto nel caso di un fronte d’onda piano precedentemente studiato.
,l’impedenza assume valore puramente reale e la sua fase è
ovviamente nulla:ci si ritrova,pertanto nel caso di un fronte d’onda piano precedentemente studiato.
Se invece r<<![]() il valore dell’impedenza si approssima allo zero,ma essa è
fortemente reattiva:ciò significa che pressione e velocità sono completamente
sfasate,determinando un’efficienza di radiazione pessima dovuta ad una riflessione di energia che ritorna sulla
sorgente sferica;
il valore dell’impedenza si approssima allo zero,ma essa è
fortemente reattiva:ciò significa che pressione e velocità sono completamente
sfasate,determinando un’efficienza di radiazione pessima dovuta ad una riflessione di energia che ritorna sulla
sorgente sferica;
Pertanto,se a titolo di esempio considero il caso di due altoparlanti,che a parità di
potenza elettrica ad essi fornita,hanno,l’uno dimensione molto piccola rispetto
a ![]() e l’altro molto
maggiore rispetto alla stessa lunghezza d’onda,avrò rispettivamente:
e l’altro molto
maggiore rispetto alla stessa lunghezza d’onda,avrò rispettivamente:
- Nel primo caso, una efficienza di radiazione molto bassa,in quanto il campo acustico è fortemente reattivo e non si accoppia con l’impedenza dell’aria in cui devo irradiare il suono
- Nel secondo caso una efficienza decisamente migliore,in quanto pressione e velocità tendono a ritornare in fase tra loro e l’impedenza Z(r) tende ad uguagliare quella meccanica del cono di cartone dell’altoparlante (e quindi quella dell’aria)
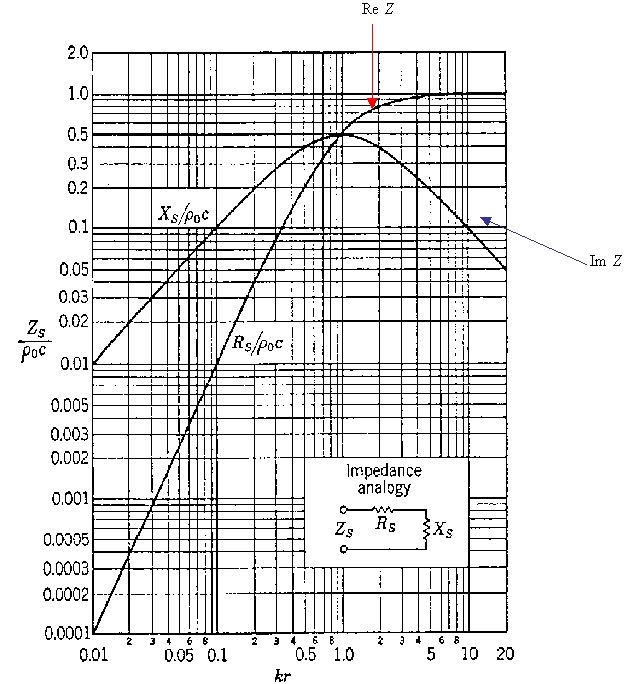
E’ opportuno,per quantificare il discorso,riportare i grafici che mostrano
l’andamento della Re[Z(r)],Im[Z(r )] e del modulo della stessa
Z(r),specificando che le ampiezze sono grandezze specifiche,cioè rapportate
all’impedenza dell’aria ![]() .
.
Figura 3:andamento della parte reale ed
immaginaria di Z(r)
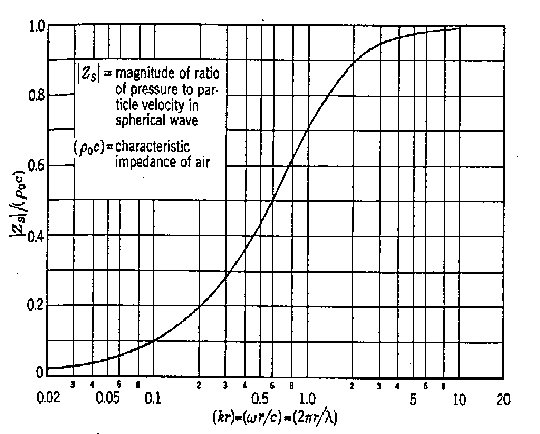
Figura 4:andamento del modulo di Z(r)
E’ interessante,inoltre mostrare l’andamento qualitativo del modulo di p ed u la cui espressione è riportata in 7 e 6 :
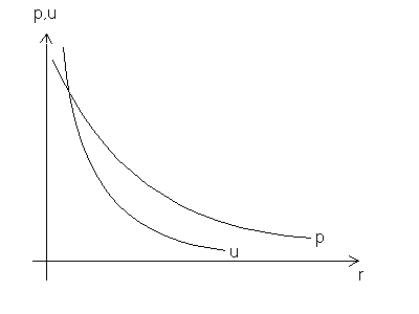
Figura 5:andamento del modulo di p ed u
Il grafico appena presentato permette di introdurre un concetto interessante riguardante i trasduttori fonici noti come microfoni;infatti,contrariamente a quello che comunemente si può pensare,non esistono solo microfoni che trasducono la pressione sonora in oscillazione elettrica,ma anche modelli che vengono costruiti per generare la medesima oscillazione elettrica in funzione della velocità dell’onda sonora captata.
Pertanto con un comunissimo microfono a pressione l’avvicinamento della sorgente sonora allo stesso ha come unico effetto l’innalzamento del segnale prodotto (e viceversa l’abbassamento se la distanza aumenta),mentre se si utilizza un microfono a velocità l’avvicinamento della sorgente causa un’esaltazione delle componenti frequenziali più gravi,mentre l’aumenta della distanza mette meglio in evidenza le componenti più acute.
Tutto ciò è noto come effetto di prossimità ed ha importanza rilevante nell’ambito musicale,specie per quello che riguarda i cantanti:
infatti se un vocalist usa un microfono a pressione,egli ha convenienza a variare la distanza dello stesso dalla sua bocca al fine di regolare l’ampiezza del suono che verrà irraggiato o registrato;se invece lo stesso cantante usa un microfono a velocità,egli può,ancora variando la distanza tra la bocca ed il microfono,decidere se esaltare un acuto o un suono più grave.(Fig. 6)

Fig 6: i cantanti usano
variare la distanza del microfono dalla loro bocca
per “equalizzare” il suono
Si può passare,ora,all’analisi energetica delle onde sferiche fin qui illustrate.
Come è già noto l’intensità istantanea di un’onda acustica è:
![]() (12)
(12)
Mentre l’intensità media è ovviamente espressa come:
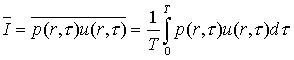 (13)
(13)
Note le espressioni di p ed u dalle 7 e 6,e grazie al fatto di avere già definito l’impedenza Z(r) posso semplificare l’espressione dellìintensità come segue:
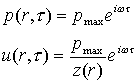 (14)
(14)
Dove ![]() è:
è:
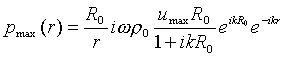 (15)
(15)
E’ utile,inoltre esprimere il
valore di ![]() nel punto
nel punto ![]() :
:
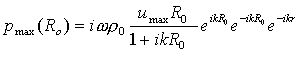 (16)
(16)
A questo punto posso effettuare l’operazione descritta in 13,la quale mi fornisce:
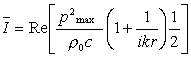 (17)
(17)
Che posso anche esprimere come:
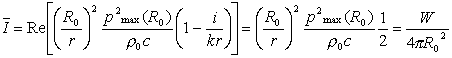 (18)
(18)
Dove W è la potenza acustica definita come l’energia sonora emessa dalla sorgente nell’unità di tempo.