
Andrea Bertolaccini 124962
UNIVERSITA’ DEGLI STUDI DI PARMA

Anno accademico 2000/2001
Corso di laurea in ingegneria delle telecomunicazioni
Corso di Fisica tecnica del docente Angelo Farina
Esercizi sullo scambio termico per conduzione
e convezione
PREMESSA
I due esercizi seguenti, svolti durante le due ore di lezione, sono utili per la comprensione dei fenomeni di scambio termico per conduzione e convezione trattati nelle lezioni precedenti. Prima di esporli può essere però d’aiuto l’analisi di alcuni casi particolari nei quali è possibile effettuare delle semplificazioni sulle grandezze in gioco. Ricordando che Nu = f(Re,Gr,Pr,x/L) si possono avere i seguenti casi:
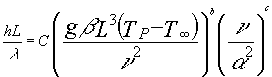
Se poi il moto è laminare allora deve anche essere c=b; quindi Nu è espresso attraverso un solo parametro cioè Nu = (GrPr)b. Il prodotto GrPr è detto numero di Raleigh (Ra);
Nu = c(RePr)a ; il prodotto RePr è detto numero di Peclet (Pe).
ESERCIZIO 1:
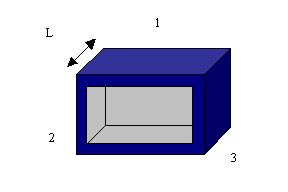
Figura 1: condotto rettangolare con aria all’interno
Si tratta di un problema di convezione naturale all’interno di un condotto rettangolare; sono forniti i seguenti dati:
T1 = 0 °C (temperatura della parete uno);
T2 = T3 = 100 °C (temperatura delle pareti due e tre);
L = 1m (lunghezza del condotto);
S1 = 2m2 (superficie della parete uno);
S2 = S3 = 1,5m2 (superficie delle pareti due e tre).
Si sà inoltre che la parete su cui poggia il condotto è adiabatica (quindi non in grado di scambiare calore) e che che dentro tale condotto è presente aria inizialmente ferma. Si chiede la temperatura Ti dell’aria all’interno (in realtà si intende la temperatura media complessiva in quei punti, altrimenti la domanda potrebbe sembrare mal posta).
Innanzitutto è bene farsi un’idea del possibile moto dell’aria nel condotto visto in sezione:

Figura 2
La circolazione sarà quindi dovuta ad una risalita periferica e ad una discesa
centrale d’aria a diverse temperature determinata dalla convezione naturale.
Facendo uso della teoria dei modelli, per la risoluzione del problema rappresentiamo la rete elettrica equivalente:
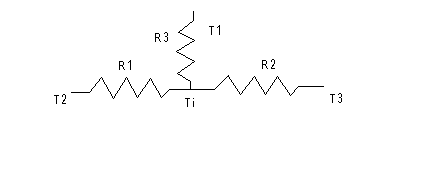 Figura 3: rete elettrica equivalente
Figura 3: rete elettrica equivalente
Siccome T2 = T3 le due resistenze R1 ed R2 sono da considerarsi in parallelo quindi la rete equivalente si riduce a:
Figura 4
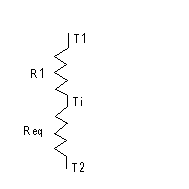
R1 ed R eq indicano le due resistenze termiche che si calcolano in questo modo:
R1 = 1/h1S1 1)
R eq = 1/2h2S2 2)
Conoscendo già le superfici dobbiamo prima di tutto calcolare i coefficienti di convezione; non essendo in regione d’ingresso ed essendo in convezione naturale, si ha in generale che Nu = cGra Prb 3)
Bisogna quindi trovare le costanti c, a, b che dipendono dalla geometria del sistema (ciò implica che quelli delle superfici verticali differiscono da quelli della parete orizzontale); con l’aiuto delle tabelle ci accorgiamo che sulle pareti poste in verticale vale la formula
Nu = 0,13Ra0,33 4)
mentre su quella posta in orrizzontale vale
Nu = 0,14Ra0,33 5)
(Ra assume lo stesso significato fisico nella convezione naturale che assume Re in quella forzata).
Essendo Ra = GrPr calcoliamo i due numeri di Grashof attraverso la formula 7):
Pr = 0,71 6)
![]()
Tale formula indica la dipendenza di Gr dalla temperatura Ti che è incognita; è necessario quindi ipotizzare una Ti* di primo tentativo (ad esempio Ti* = 60 °C) e fare i calcoli verificando che sia una previsione attendibile. A tale temperatura corrispondono una viscosità cinematica di 1,89∙10-5 ed una costante beta (1/T) di 1/333. Si ha quindi:
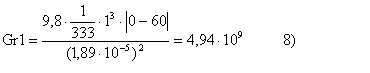
Se poi calcolo
Ra1 = GrPr = 3,5∙109 > 109 9)
mi accorgo che il regime risulta turbolento e che la formula 5), valida proprio in questa condizione è lecita.
Si ottiene quindi il numero di Nusselt (ricordo che il pedice 1 si riferisce sempre alla parete posta in orrizzontale mentre il pedice 2 a quelle poste in verticale):
Nu1 = 0,14(3,5∙109)0,33 = 197,79 10)
Essendo poi:
Nu1 = h1 L /l aria 11)
ricavo h1 = Nu1 l aria / L = 197,79 . 0.028 / 1 = 5,54 W/m2K 12)
dove l aria = 0.028 W/mK
Calcoli del tutto analoghi ci permettono di trovare:
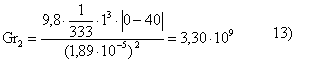
Ra2 = Gr Pr = 3,3 . 109 . 0,71 = 2,34 109> 109 14)
Nu2 = 0,13 (3,3 . 109) 0,333 = 160,6 15)
h2 = Nu2 l aria / L = 4,5 W/m2K 16)
Essendo Q il flusso di calore che passa attraverso la rete equivalente di figura 4, ottengo ora la Ti cercata:
Q = (T2 – T1)/[(1/h1S1)+(1/2h2S2)] = (Ti – T1)/h1S1 =>
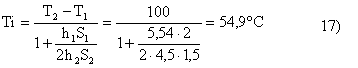
Questo valore differisce troppo da quello stimato (del 9,3 %); proviamo quindi a rifare gli stessi conti con un seconda temperatura di tentativo Ti** = 54,9 °C:
Gr1 = 4,61∙109 Ra1 = 3,27∙109 => Nu1 = 193,17
Gr2 = 3,77∙109 Ra2 = 2,68∙109 => Nu2 = 167,87
I due nuovi coefficienti di convezione sono quindi:
h1 = 5,41 W/m2K e h2 = 4,70 W/m2K
Si trova ora un valore Ti = 56,7 °C che differisce solo del 3,27% ed è perciò accettabile.
ESERCIZIO 2:
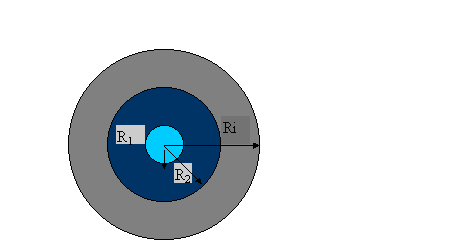 Figura 5:
Figura 5:
condotto circolare metallico
Si tratta di un problema combinato di scambio termico conduttivo/convettivo, di fluidodinamica e termodinamica. Si cerca di isolare un condotto circolare metallico (acciaio) dentro al quale scorre dell’ acqua; sono dati:
R1 = 13mm (raggio interno del condotto);
R2 = 17mm (raggio esterno del condotto);
L = 1m (lunghezza del condotto);
Tacqua = 5 °C;
j ¥ = 0,5 (grado igrometrico);
T¥ = 20° C (temperatura ambiente);
W = 1m/s (velocità dell’acqua nel tubo);
Ri = ? (raggio dell’isolante, incognita del problema).
Il carattere igrometrico del problema ci porta a definire una temperatura di rugiada
Tr = 9 °C; ciò ci fa capire che la temperatura esterna dell’isolante Tpe deve essere maggiore di Tr altimenti l’aria che lambisce il condotto formerebbe delle goccioline d’acqua per condensazione che causerebbero poi la ruggine e tutti i problemi che da essa possono seguire. Si comprende allora l’importanza di un buon isolamento termico e quindi la determinazione di un Ri adeguato.
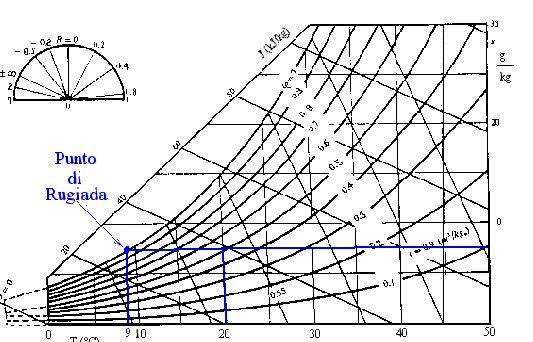
Figura 6: diagramma psicrometrico relativo alla pressione atmosferica
Ricaviamo dalle tabelle i valori di:
l
i= 0,04 ![]()
l
acciaio=75![]()
Studiamo innanzitutto il problema dal punto di vista termico:
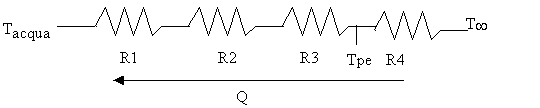
Figura 7: rete elettrica equivalente
con:
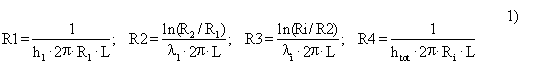
htot tiene conto anche del fenomeno dell’irraggiamento seppur non ancora studiato.
.
Calcoliamo quindi i coefficienti di convezione:
per l’acqua all’interno del tubo (convezione forzata) si usa l’equazione di Dussel Boelter
Nu = 0,023Re0,8Pr0,4 2)
Sarebbe stato Nu = 0,023Re0,8Pr0,3 se fosse il fluido a cedere calore ma nel nostro caso è l’acqua ad essere riscaldata.
Il numero di Reynolds risulta essere:
![]()
Il regime è quindi turbolento; Pr è tabellato e per l’acqua a 5 °C vale 12,2.
Nu1 = 0,023(17000)0,8(12,2)0,4 = 152 4)
Essendo poi
Nu1 =h1 D1 /l 5)
Þ h1 = Nu1 l / D1 =3332 W/m2K ; l = 0,57 W/mK 6)
Siccome Tpe è funzione di Ri che è incognita, dovremo procedere per tentativi fissando un primo valore verificandone poi la sua idoneità; prendiamo ad esempio per cominciare Ri* = 20mm.
La convezione all’esterno del tubo è naturale; si ha quindi:
Nu = 0,53Gr0,25Pr0,25 (valide in regime laminare) 7)
![]()
Perciò:
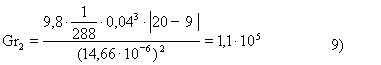
Dove DI = 40mm = 0,04m (diametro isolante ossia lunghezza caratteristica) e ß = 1/288 poichè è stata considerata la temperatura media dell’aria che lambisce l’isolante Tm = 15 °C circa;
=> Nu2 = 0,53(1,1∙105)0,25(0,71)0,25 = 8,7 10)
Dunque: h2 = Nu2 l / D1 =5,2 W/m2 K con l =0,04 W/m2K 11)
Risulta h1>>h2 che potrebbe anche essere trascurato ; nel considerare htot e quindi il contributo irraggiante, raddoppio approssimativamente il valore trovato, operando in questo modo una stima che si rivelerà in seguito accurata.
=> htot = 2 h2 = 10 W/m2K circa 12)
Sono ora in grado di calcolare il flusso di calore:
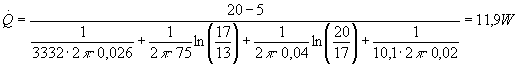 13)
13)
Nel calcolare Rtot si sono considerate tutte e quattro le resistenze termiche anche se R1 ed R2 sono molto piccole rispetto alle altre due (si potevano perciò trascurare).
Concludendo, grazie alla legge di Ohm, ricaviamo la Tpe cercata:
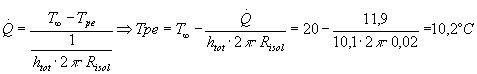 14)
14)
Si ottiene dunque una temperatura di 1,2 °C superiore a quella di rugiada, il che è un margine di sicurezza; con la scelta fatta di un Ri* = 20 mm si ha perciò un buon isolamento termico del condotto metallico.
Vengono di seguito riportate le tabelle relative alle formule e ai dati usati durante lo svolgimento dei due problemi:
|
Campo di validità: (RE) |
Ing. Dinamico |
Ing. Termico |
Regime Sviluppato |
Costante in parete
T Q |
Calcolo del Numero di Nusselt NU = C Rea Prb
C a b |
Autori |
|||
|
< 2300 |
· |
· |
· |
0.289 (D/X)1/2 |
0.5 |
0.33 |
Elser |
||
|
< 2300 |
|
· |
· |
1.86 (D/X)1/3 |
0.33 |
0.33 |
Sieder e Tate |
||
|
< 2300 |
· |
· |
· |
0.664 (D/X)1/2 |
0.5 |
0.33 |
Pohlhausen |
||
|
3000-30000 |
· |
· |
0.0033 |
1 |
0.37 |
Bohm |
|||
|
2700-7000 |
· |
· |
· |
0.01 (D/X)0.37 |
1 |
0.37 |
Giulianini e al. |
||
|
>10000 |
· |
· |
0.036 (D/X)1/18 |
0.8 |
0.33 |
Nusselt |
|||
|
>10000 |
· |
0.032 (D/X)1/20 |
0.8 |
0.37 |
Kraussold |
||||
|
>10000 |
· |
0.032 (D/X)1/20 |
0.8 |
0.30 |
Kraussold |
||||
|
>10000 |
· |
0.183 (D/X)1/3 |
7/12 |
0.33 |
Elser |
||||
|
>10000 |
|
· |
· |
0.023 |
0.8 |
0.4 |
Dittus e Boelter |
||
|
>10000 |
· |
· |
0.023 |
0.8 |
0.3 |
Dittus e Boelter |
|||
|
>10000 |
· |
· |
0.027 |
0.8 |
0.33 |
Sieder e Tate |
|||
|
12000-220000 |
· |
· |
0.02 (DI/DE)0.53 |
0.8 |
0.33 |
Monrad e Pelton |
|||
Tabella 1: formule sperimentali per il calcolo del numero di Nusselt in condizioni di convezione forzata
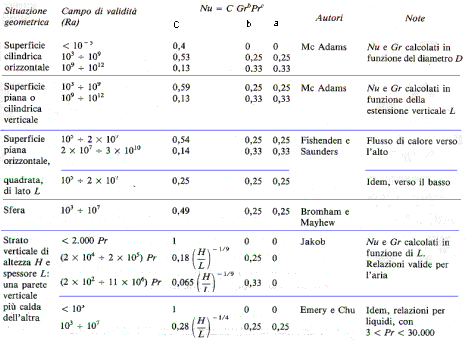
Tabella 2: formule sperimentali per il calcolo del numero di Nusselt in
convezione naturale
|
Temperatura |
Calore Specifico (p cost) |
Densità |
Viscosità Dinamica |
Conduttività Termica |
Numero di Prandtl |
|
|
T |
cp |
r |
m |
l |
Pr |
|
|
°F |
°C |
KJ/kg× °K |
kg/m3 |
kg/m× s × 10-3 |
W/m× °K |
|
|
32 |
0 |
4.225 |
999.8 |
1.79 |
0.566 |
13.25 |
|
40 |
4.44 |
4.208 |
999.8 |
1.55 |
0.575 |
11.35 |
|
50 |
10 |
4.195 |
999.2 |
1.31 |
0.585 |
9.40 |
|
60 |
15.56 |
4.186 |
998.6 |
1.12 |
0.595 |
7.88 |
|
70 |
21.11 |
4.179 |
997.4 |
0.98 |
0.604 |
6.78 |
|
90 |
26.67 |
4.179 |
995.8 |
0.86 |
0.614 |
5.85 |
|
100 |
32.22 |
4.174 |
994.9 |
0.765 |
0.623 |
5.12 |
|
110 |
37.78 |
4.174 |
993.0 |
0.682 |
0.630 |
4.53 |
|
120 |
43.33 |
4.174 |
990.6 |
0.616 |
0.637 |
4.04 |
|
121 |
48.89 |
4.174 |
988.8 |
0.562 |
0.644 |
3.64 |
|
130 |
54.44 |
4.179 |
985.7 |
0.513 |
0.649 |
3.30 |
|
140 |
60 |
4.179 |
983.3 |
0.471 |
0.654 |
3.01 |
|
150 |
65.55 |
4.183 |
980.3 |
0.43 |
0.659 |
2.73 |
|
160 |
71.11 |
4.186 |
977.3 |
0.401 |
0.665 |
2.53 |
|
170 |
76.67 |
4.191 |
973.7 |
0.372 |
0.668 |
2.33 |
|
180 |
82.22 |
4.195 |
970.2 |
0.347 |
0.673 |
2.16 |
|
190 |
87.78 |
4.199 |
966.7 |
0.327 |
0.675 |
2.03 |
|
200 |
93.33 |
4.204 |
963.2 |
0.306 |
0.678 |
1.90 |
|
220 |
104.4 |
4.216 |
955.1 |
0.267 |
0.684 |
1.66 |
|
240 |
115.6 |
4.229 |
946.7 |
0.244 |
0.685 |
1.51 |
Tabella 3: proprietà termofisiche dell’acqua
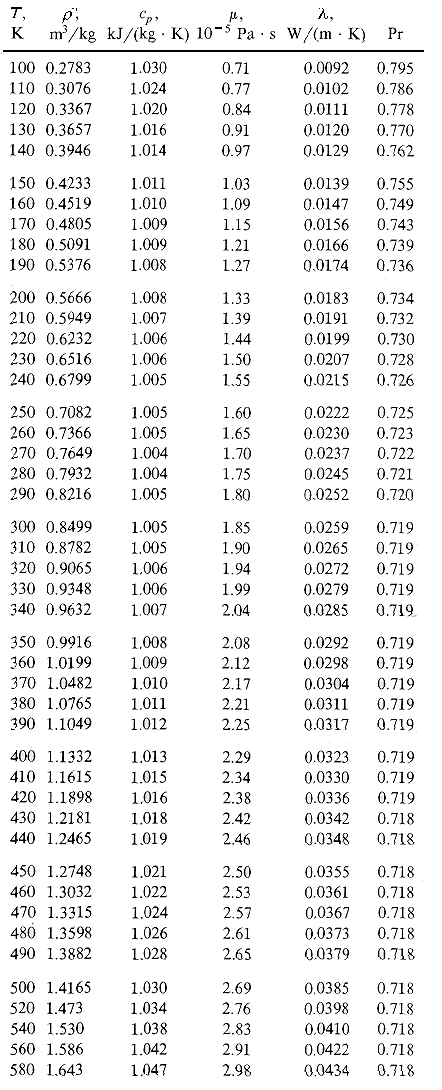
Tabella 4: proprietà termofisiche dell’aria