Lo studio dei transitori termici implica l’analisi di una evoluzione spaziale e temporale della temperatura. Questo tipo di problema richiede, per la sua risoluzione ,strumenti matematici il cui utilizzo risulta essere spesso complicato; sono infatti necessarie le equazioni differenziali, le quali sono raramente risolubili per via analitica. Per ovviare a questo problema si utilizzano tecniche fornite dal calcolo numerico, che seppur non forniscano la soluzione esatta rendono facilmente disponibili soluzioni approssimate che possono essere anche molto accurate.

Prendiamo per esempio una lastra piana ed indefinita di spessore s che per t <0 si trova alla temperatura T=T₀ e in seguito al tempo t =0 andremo ad immergere in olio bollente. Operiamo usando il metodo delle differenze finite: discretizziamo lo spessore della lastra suddividendola in una successione di strisce di spessore D x e abbiamo:

(1)

dove:

• s è lo spessore totale della lastra
• D x è lo spessore di una striscia
• N_d è il numero di suddivisioni in strisce

Rappresentiamo la situazione con il seguente schema:

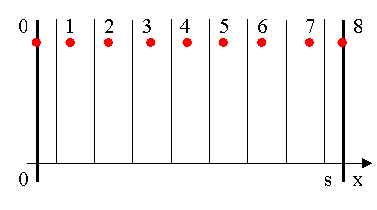
Figura 1 – Discretizzazione geometrica della piastra

Supponiamo ad esempio di suddividere lo spessore della lastra in 7 strisce e operiamo la suddivisione in modo tale che ogni striscia abbia spessore D x tranne quelle adiacenti alla pelle della lastra che saranno prese di spessore D x/2.Individuiamo quindi dei punti particolari che chiameremo nodi prendendo il primo e l’ultimo sulle facce della lastra mentre quelli interni al centro di ciascuna striscia.

Operando in questo modo tutti i nodi sono distanti D x tra loro e saranno pari al numero di strisce meno una.

I nodi sono punti molto importanti perché approssimiamo la temperatura dell’intera striscia con la temperatura del nodo che contiene, in questo modo possiamo trascurare le variazioni di temperatura che si hanno tra un lato e l’altro di una stessa striscia.

Abbiamo dunque effettuato una discretizzazione spaziale ; l’ascissa x è cioè una variabile discreta e vale la relazione :

(2)

dove i è un numero intero non negativo che chiamiamo indice di nodo. (i=0…N_d)

Effettuiamo anche una discretizzazione temporale; per questo dobbiamo prendere un opportuno passo temporale D t e vale la relazione:

(3)

dove t è l’indice di tempo.

Per risolvere il transitorio ci serviremo di una matrice bidimensionale di questo tipo:

Figura 2

Per indicare la temperatura di un nodo ad un certo istante temporale useremo la notazione :

dove l’apice è l’indice di tempo e il pedice è l’indice di nodo.

Vogliamo ora trovare l’algoritmo che permetta di stimare il profilo delle temperature al passo temporale successivo dalla conoscenza delle temperature di ogni nodo al passo corrente.

Rifacciamo la costruzione dell’equazione di Fourier concentrando la nostra attenzione su un generico nodo a un generico istante di tempo.

Dobbiamo scrivere la variazione di temperatura in funzione dei flussi di calore sulla faccia destra e sinistra usando il principio di conservazione dell’energia:

(4)

dove :

- è la quantità di calore entrante dal lato sinistro della striscia

- è la quantità di calore uscente dal lato destro della striscia

D’altra parte sappiamo che :

  (5)

che discretizzando la derivata diventa:

(6)

(7)

Da queste uguaglianze la (4) diventa:

(8)

avendo ipotizzato

Da questa equazione ricaviamo la temperatura al tempo t+1 e ottengo:

(9)

Ci poniamo ora il problema di vedere se l’intervallo temporale D t possa essere preso grande a piacere. Notiamo che se D t fosse troppo grande il coefficiente che moltiplica potrebbe diventare negativo; se ciò accadesse l’equazione diventerebbe numericamente instabile dando luogo ad oscillazioni. L’instabilità dell’equazione non è però causata dall’inaccuratezza del nostro modello ma è dovuta a cause fisiche; la temperatura del nodo n è infatti destinata a crescere ma se il coefficiente di fosse negativo potrebbe anche diminuire contraddicendo il secondo principio della termodinamica.

Esiste dunque un valore limite di D t che si ottiene ponendo nullo il coefficiente di e vale:

(10)

essendo

una grandezza che rappresenta la rapidità di propagazione delle variazioni di temperatura nel materiale detta diffusività termica.

In questa tecnica ,detta TIME MARCHING, permette inoltre di simulare una velocità di propagazione del calore

che diminuisce al diminuire di D x.

Se nella (9) usiamo D t _lim questa diventa:

(11)

che è la media aritmetica tra le temperature dei nodi adiacenti.

Questa scelta di D t è probabilmente un po’ troppo "grossolana", infatti per il calcolo di non si tiene conto di .

Si usa scegliere il D t ottimale che è uguale ai 2/3 del D t limite.

Con questa scelta la (9) diventa:

(12)

Dove a causa di un passo temporale più piccolo devo eseguire un numero maggiore di operazioni ma ottengo una soluzione più accurata.

Consideriamo una lastra di spessore s=12 cm che al tempo t =0 si trova alla temperatura T₀=38°C e che viene successivamente immersa in olio bollente che impone una temperatura di parete T_p=260°C. E’ noto anche il valore di diffusività della lastra che vale .

Il nostro obbiettivo è trovare T(x) nei primi tre minuti e per questo adottiamo una discretizzazione spaziale con 9 nodi e prendiamo inizialmente come intervallo temporale:

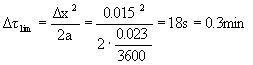
Devo quindi considerare 10 passi temporali perché il transitorio da studiare è di 3 minuti e il passo temporale di 0.3 minuti.

Supponendo che i nodi situati sulla pelle vadano istantaneamente alla temperatura di 260°C, andiamo a calcolare le temperature con una tabella in cui in ogni cella è riportata la temperatura di un nodo, in un determinato istante temporale, la quale è data dalla media aritmetica delle temperature dei nodi adiacenti all’istante temporale precedente.(stiamo usando il D t limite)

Tabella 1

Nota:

All’inizio del transitorio i nodi interni alla lastra rimangono alla temperatura iniziale di 38°C,poi la temperatura aumenta dall’esterno verso l’interno in modo simmetrico.

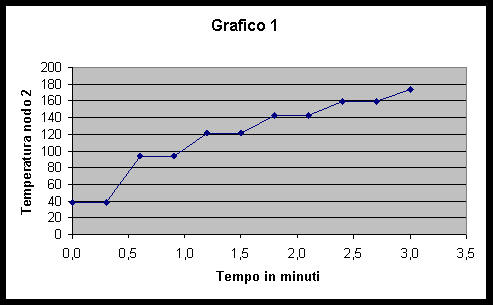
Dal grafico notiamo che in passo temporale ogni due ho un mantenimento della temperatura dell’istante temporale precedente. Questo andamento "a pianerottoli" è dovuto alla scelta di D t ; se invece operiamo una scelta migliore di D t prendendo ad esempio D t ottimo dobbiamo considerare un numero maggiore di passi temporali essendo:

dovremo quindi considerare 15 passi temporali.

Tabella 2

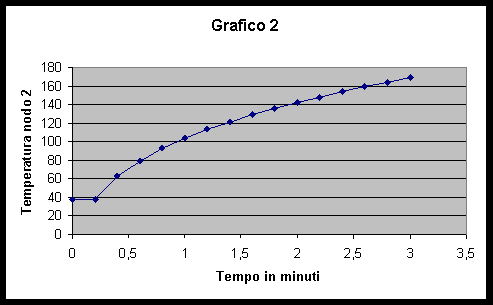
In questo caso il grafico è strettamente crescente.

Ci si trova però spesso di fronte a problemi nei quali la condizione che i nodi esterni vadano subito alla temperatura di regime non è realistica.

Possiamo schematizzare la situazione in questo modo:

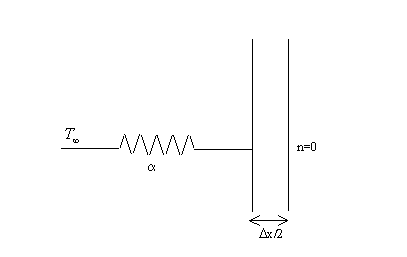Figura 2

dove a è il coefficiente di convezione.

In questa nuova situazione anche la temperatura dei due nodi esterni è incognita, devo dunque utilizzare una nuova equazione di calcolo che tenga conto anche di queste due nuove incognite.

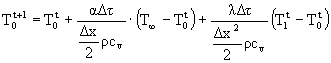
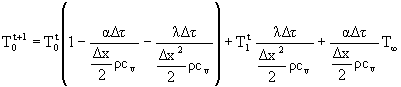(13)

Il coefficiente di non può essere negativo quindi se a è grande D t _lim per il primo nodo diventa molto più piccolo che per i nodi interni. Sulla superficie ho dunque un punto di instabilità locale e dovrò scegliere come passo temporale per tutta la discretizzazione quello più piccolo imposto dal nodo superficiale:

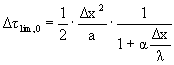(14)

dove è un numero puro caratteristico dei transitori termici detto numero di Biot.

Il numero di Biot è un’importante indicatore di come dobbiamo affrontare un problema di transitorio termico, infatti:

Se Biot<0.1 dobbiamo considerare anche convezione e irraggiamento tra la superficie

della lastra e l’ambiente esterno

Se Biot>40 possiamo considerare soltanto il fenomeno conduttivo

Fino a questo punto abbiamo usato un metodi espliciti per risolvere transitori, ma è possibile anche usare metodi impliciti.

Riprendendo la (8) e ragionando dal futuro verso il presente ho:

(15)

e scrivendo N-1 equazioni di questo tipo ho un sistema lineare con N-1 equazioni e N-1 incognite e quindi risolubile.

Riscrivendo la (15) nel seguente modo:

n=1…N-1 (16)

posso facilmente scrivere il sistema in modo matriciale del tipo:

(17)

dove A è una matrice tridiagonale con gli elementi della diagonale tutti uguali pari al coefficiente di della (16).

Notiamo che questo coefficiente è sempre positivo, quindi il metodo implicito è sempre stabile e per questo non esiste un D t _lim.

Moltiplicando ambo i membri della (17) per la matrice A^-1 ,inversa di A, ottengo:

(18)

in questo modo ricavo le temperature nuove da quelle vecchie.