Diapositiva 1

S[k]: Inverse filter

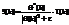
G[k]: smoothed and spectrally decimated version of the system measured transfer function.

ε: regularization parameter. has been taken (typically) equal to 0.01

T[k] : target curve.

Marco Binelli1, Angelo Farina2
1 University of Parma, Industrial Eng. Dept., Parco Area delle Scienze 181/A, 43100 PARMA, ITALY
drumboogie@gmail.com
2 University of Parma, Industrial Eng. Dept., Parco Area delle Scienze 181/A, 43100 PARMA, ITALY
farina@unipr.it

Digital equalization of automotive sound systems
employing spectral smoothed FIR filters

The usage of traditional inversion techniques gives FIR filters longer or equal than the measured impulse response. Because of the limited DSP computing power in automotive field, we aim to reduce the filter length by spectral smoothing, as previously observed by [1]. Other advantages of this method are a remarkable enlargement of the sweet spot and the stability of the equalization

We developed a graphic Matlab1 function suite. It allows to plot the measured frequency response and set all the filter parameters (length, spectral resolution, target curve, regularization parameters)

1 Matlab is a registered trademark of The MathWorks, Inc.

A blind listening test was performed to investigate on subject’s filters liking. The 9 involved persons were medium-high skilled. In detail, we chose some target curves and averaging windows and asked the subjects to fill a questionnaire

The smoothing algorithm is the same of [1]. It means that there is an independent computing for magnitude and phase and this translates in a non-linear complex averaging

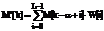
M: variable (magnitude or phase) to be smoothed

M’: smoothed variable

L: window length

α: half window length (L=2α+1)

W: window shape

Equation 1: magnitude/phase smoothing

The inversion technique is based on [3]. This ensures a correct phase handling and absence of strong peaks in the filter spectrum. The inverse filter S[k] can be computed as follow:

Equation 2: Inverse filter synthesis

We used some variable window lengths rules: Critical Bands (CB), Equivalent Rectangular Bandwidths (ERB), Double Octave Fraction (DOF) bands (1/24 octave below the car Schroeder frequency, ≈ 800 Hz, 1/3 octave above).

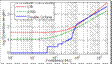
Figure 1: averaging window length vs frequency

Figure 2: magnitude plots shown after filter computation

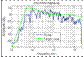
Figure 3: magnitude of a frequency response and target curve

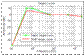
Figure 4: target curves used to build
the test filters

Figure 5: some measured spectra
of test filters

Figure 6: evaluation questionnaire
(D, E, F filter omitted)

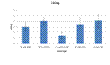
From Student’s t test we can say that the filters with “hard” target curve are the best between the tested configurations. You can see this from the Student’s t test (raw A B, table 1) and from the relationship between “spectral distance” and “liking” (figure 8).

It is difficult to establish directly if there is an averaging window better than another but it is possible to say that filters liking increases with the smoothness of the spectrum (figure 9). Further investigations will be done on smoothness types.

Other interesting results come from subjective parameters relationships. We found 5 adjective well related to the global filters liking (two are shown here, figure 10 and 11)

The resolution of the questions scale was just 5 discrete steps, so it was hard to compare between average values results because of the big standard deviation as you can see in figure 7.

Figure 7: “filter type-liking” histogram with standard deviation indicators

Figure 8: “spectral distance - liking” relationship

Figure 9: “spectral roughness - liking” relationship

Table 1: Student’s t test on “Liking” parameter

Figure 10: “liking - bass balance” relationship

Figure 11: “liking - warmth” relationship

Filter couple

Random Percentage

A B

0,22%

B C

< 0,01%

C D

0,01%

D E

16,00%

A C

< 0,01%

A D

34,80%

A E

1,83%

B D

11,54%

B E

84,87%

C E

< 0,01%

We tested inverse filters with 2 target curves (“Soft” and “Hard”) and 3 averaging windows (ERB, CB, DOF). Over these, the native car sound configuration (not filtered) was inserted inside the listening test.

This is the test filter set:

A – Soft + ERB;

B – Hard + ERB;

C – Native (not filtered);

D – Soft + DOF;

E – Hard + CB.

This work was supported by:

AES 125 Convention

Paper 7575

In this paper we investigate about the usage of spectral smoothed FIR filters for equalizing a car audio system. The target is also to build short filters that can be processed on DSP processors with limited computing power. The inversion algorithm is based on the Nelson-Kirkeby method and on independent phase and magnitude smoothing, by means of a continuous phase method as Panzer and Ferekidis showed. The filter is aimed to create a "target" frequency response, not necessarily flat, employing a little number of taps and maintaining good performances everywhere inside the car's cockpit. As shown also by listening tests, smoothness and the choice of the right frequency response increase the performances of the car audio systems.