
Brahma

Soundfield SPS-200
DPA-4

Core Sound TetraMic
(C) by Angelo Farina, University of Parma, Italy
This page deals with the problem of converting the 4 signals coming from the capsules of a Soundfield-like microphone, collectively called A-format, to a standard B-format signal, either in FuMa or Ambix variants. FuMa stands for Furse-Malham, Ambix also stands for ACN-SN3D. Both are variants of the B-format concept, which is explained here below.
First of all, these Soundfield-like A-format microphones employ 4 cardioid or subcardioid capsules, arranged (more or less) as a tetrahedron, as shown in the following pictures:
 Brahma |
 Soundfield SPS-200 |
DPA-4 |
 Core Sound TetraMic |
The first thing is to label and number the signals from the 4 capsules, which constitute the A-format stream, for avoiding to process them improperly.
We assume to employ an anthropometric Cartesian reference system (compliant with ISO 2631), as shown here:
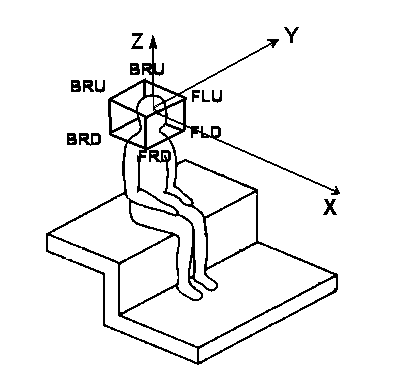
We can think that the 4 capsules are at 4 of the 8 vertexes of a cube, which surrounds the head of the "virtual listener". This cube has faces parallel to the above Cartesian reference system. We can call the faces with positional names, such as Front-Back , Left-Right and Up-Down. Each vertex of the imaginary cube is defined by the intersection of three faces, and so, for example, a microphone pointing to Front, Left, Up will be labelled FLU.
There are two possible ways of selecting the positions for the 4 capsules on the cube:
FLU-FRD-BLD-BRU (Soundfield was the first to use this layout, all the others shown above use this too, and also Ambeo from Sennheiser)
FLD-FRU-BLU-BRD (DPA-4 was originally using this, but my one was modified for complying with the Soundfield standard)
What follows is mostly referred to the Brahma microphone. When we connect the 4 microphones to a recorder (the recommend ones are the Zoom F8 or F4), we can in theory choose any order for wiring the channels. But in the case of the Brahma microphone, the order which is usually employed is the following:
- Channel 1: FLU
- Channel 2: FRD
- Channel 3: BLD
- Channel 4: BRU
Be aware, other microphones can employ a different channel ordering. You are suggested to check the documentation of your microphone!
We now record the 4 channels coming from the capsules, and we want to derive, by proper processing, the 4 channels of a standard old-style B-format stream, named W, X, Y and Z, with Furse-Malham channel ordering and Furse-Malham amplitude scaling. Be aware that, for VR applications (Youtube, Facebook, etc.) the Furse-Malham conventions are not employed, instead you need to to use ACN channel ordering and SN3D amplitude scaling (Ambix format). But in the end this just means to employ a different filter matrix, which can easily be obtained modifying the FuMa matrix, as explained at the end of this page...
These 4 B-format signals are matematically defined as the signals of 4 coincident microphones. W is a pressure microphone (omnidirectional), whilst X, Y and Z are velocity microphones, having a directivity pattern resembling a figure-of-8. The following picture shows the prescribed directivity patterns for these microphones:
 Axes |
 W |
 X |
 Y |
 Z |
The basics of the conversion from A-format to B-format is to perform the convolution of the recorded signals with a matrix of 4x4=16 FIR filters.

Here M=4, V=4 ad hence the filter matrix is 4x4.
It is outside the scope of this page to explain how to create such a filter matrix, but a good starting point can be the "virtual microphone" theory explained in detail in this paper.
So the filtering formulas are:
W = FLU*f(1,1) + FRD*f(1,2) + BLD*f(1,3) + BRU*f(1,4)
X = FLU*f(2,1) + FRD*f(2,2) + BLD*f(2,3) + BRU*f(2,4)
Y = FLU*f(3,1) + FRD*f(3,2) + BLD*f(3,3) + BRU*f(3,4)
Z = FLU*f(4,1) + FRD*f(4,2) + BLD*f(4,3) + BRU*f(4,4)
The filters are actually WAV files. A single 4-channels WAV file can contain all the 16 filters, packed in the so-called "matrix format", which is recognixed perfectly by X-volver, as shown here:
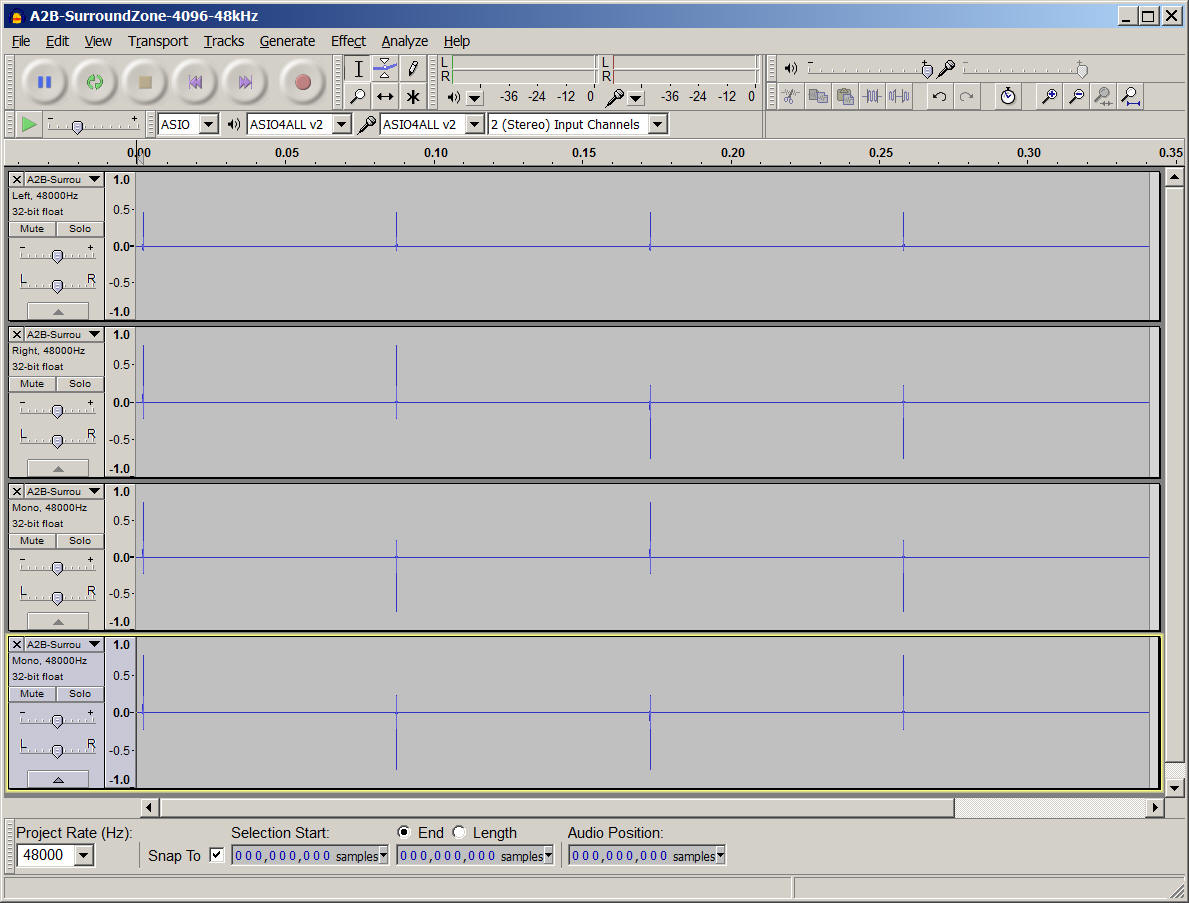
The filter matrix shown here is the one for the Soundfield SPS-200 microphone. Generally speaking, each A-format microphone should require its own "personalized" filter matrix. The Brahma microphones are individually measured in anechoic conditions, and an unique set of A2B conversion filters is generated for each unit being manufactured. Other makers, such as Soundfield, or Sennheiser (Ambeo) provide "generic" A2B filters, which of course operate sub-optimally. Coresound provides generic filters, but, on demand, can provide individual filters based on anechoic measurements. The DPA-4 is sold "without filters", and it is left to the owner of the microphone to measure it and compute his own matrix of A2B filters. Several of these A2B filter matrices can be found together with the X-volver VST plugin, which is employed for actually performing the convolution in realtime.
More info and downlod link for the VST plugin and several filter matrices here: X-volver
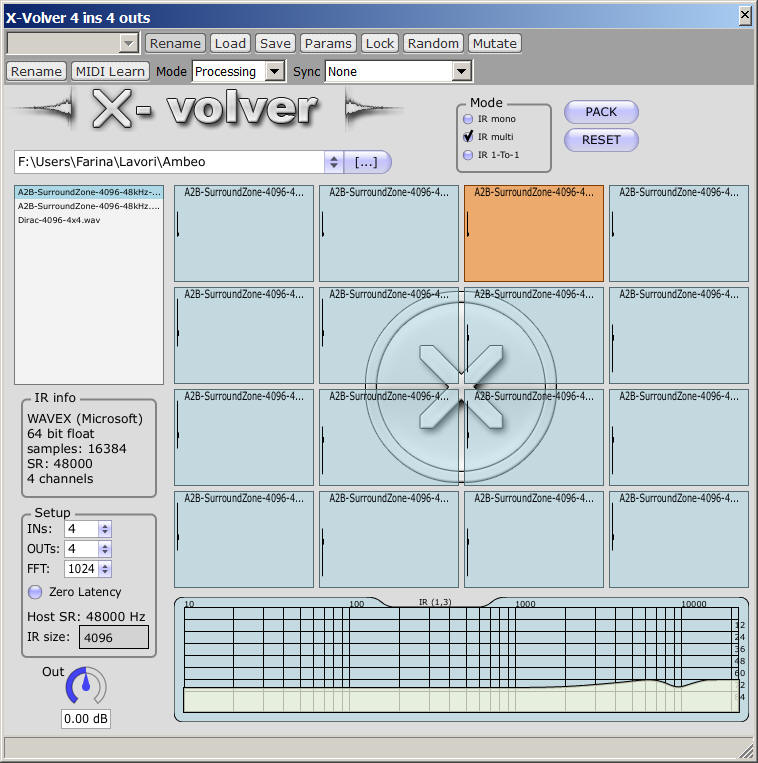
Here you can see the GUI of Xvolver, set up with 4 inputs and 4 outputs, when loaded with the A2B filter matrix shown above:
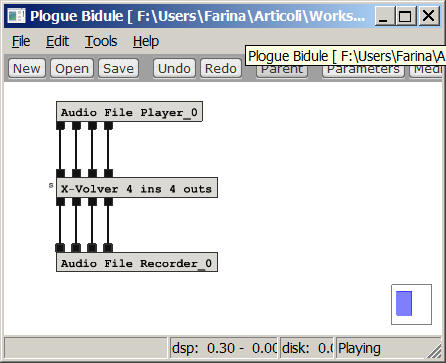
And here you see the host program suggested for this A2B conversion, Plogue Bidule, loaded with the X-volver VST plugin (but many other host programs can be used instead of Plogue Bidule, if preferred, such as Audio Mulch or Reaper):
And what if instead of a plain, old B-format you instead need to create an Ambix output for getting a "spatial audio" soundtrack of immersive panoramic videos to be seen with the Google Cardboard on Youtube?
See a couple of examples here:
You just need to edit your filter matrix, and save it again after editing inside Audacity. The modifications to be done are:
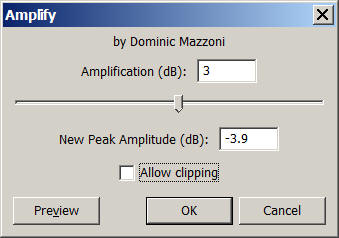
1) Amplify by +3dB the first channel (W)
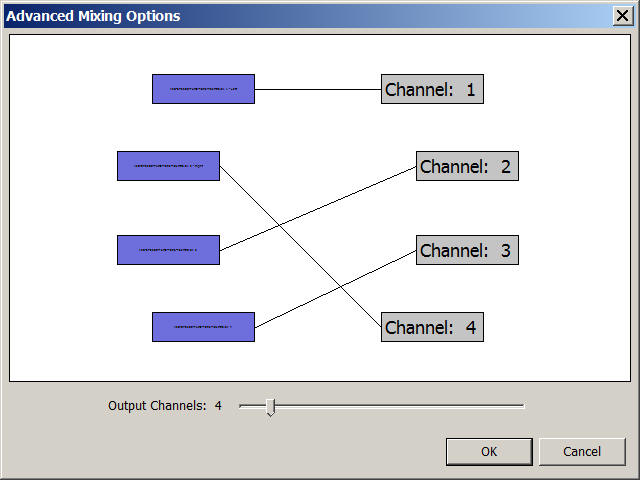
2) Rearrange the channel order, as in Ambix, instead of WXYZ, the channel order is WYZX. This can be done when you export your 4-channels audio to a new WAV file and this will be your new filter matrix in Ambix format.
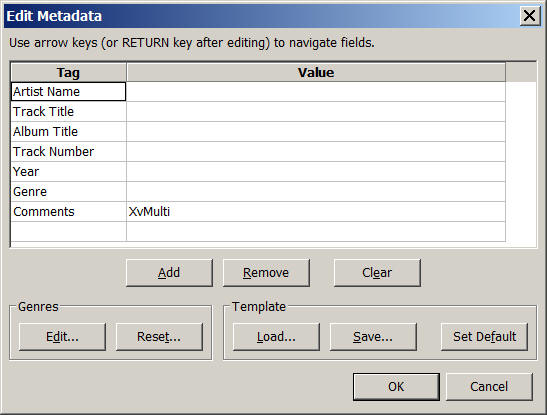
Just remember that in Audacity you have to specify "XvMulti" in the Comments, if you want that your filter matrix is recognized properly by the MAC-OSX version of X-volver (the Windows version does not require this):
For more information about measurement technique and computation of the filter matrix for your own A-format microphone, you can contact Angelo Farina.
All the contents are Copyright by Angelo Farina, 2017