M E T O D I D I M I S U R A F L U I D O D I N A M I C I

Gli strumenti di misura che tratteremo sono divisi in due categorie:

1- INTEGRALI:misurano l’intera portata di fluido che scorre nel condotto; un esempio di misuratore di questa categoria è il TUBO DI VENTURI;

2- LOCALI: misurano la velocità di un singolo filetto fluido di ridotte dimensioni rispetto all’intero diametro di passaggio; un rappresentante di questo tipo è il TUBO DI PITOT.

Questi sono i due metodi più interessanti anche se per poterli tarare dobbiamo ricreare una situazione molto più semplice, dobbiamo però tener presente che il metodo più preciso per analizzare l’intera portata di un tubo è il metodo della PESATA. Con questo sistema vengono tarati tutti gli altri strumenti di lavoro e ci consente una misura molto più economica e comunque precisa.

Per realizzare questa taratura necessitiamo di un secchio, un tubo dell’acqua con rubinetto, un cronometro ed un po’ di nostra precisione. Apriamo l’acqua ed allo stesso istante facciamo partire il cronometro, quando il secchio sarà pieno dovremmo bloccare i secondi passati, a questo punto non ci resta che pesare il secchio di cui avremo precedentemente preso la tara e calcolare la differenza di peso dalla quale sappiamo il peso dell’acqua espresso in chilogrammi (Kg). Il tempo misurato sarà invece espresso in secondi (s).

Questa grandezza è identificata come PORTATA IN MASSA e si indica

Se voglio tarare un sistema di misura (ad esempio il Tubo di Venturi), lo colloco

al posto di una parte di tubo, in questo modo faccio la misura della portata col tubo di Venturi e simultaneamente, col secchio ed il cronometro applico il metodo della pesata. Verificò così la funzionalità dello strumento di misura che ho inserito nel condotto (vedi figura a seguito)

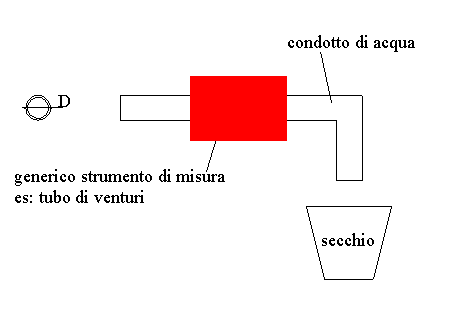fig.1

Dobbiamo ricordare il legame tra la velocità del fluido, la sua portata, e il diametro del condotto. Questo legame è espresso dalla relazione:

in cui è la densità, W è la velocità media di scorrimento e A è l’area di passaggio, D il diametro; come appena scritto sappiamo quindi che A è l’area del cerchio dato dalla sezione del tubo di diametro D. quando negli esercizi si parlerà di sezione di passaggio si intenderà l’area della sezione del condotto.

Si deve ricordare anche la densità di due sostanze fondamentali:

1- l’acqua:

2- l’aria:

La densità di quest’ultima, che è un gas, non ha sempre lo stesso valore, anzi questo cambia molto a seconda della pressione e della temperatura. In ogni caso la densità dei gas perfetti si ricava dalla seguente relazione:

dove P è la pressione, R è la costante del gas e T la temperatura espressa in gradi Kelvin.

T U B O D I V E N T U R I

Fig.2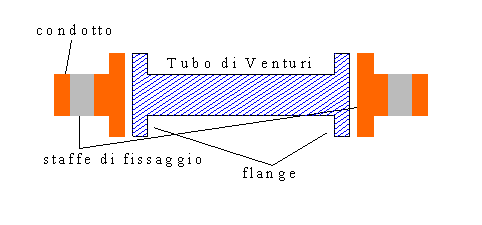 Passiamo ora a vedere come è fatto il tubo di Venturi, esso è un pezzo di tubo che si monta (come si vede nella figura in alto) al posto di una parte del condotto dritta. E’ un elemento montato tra due flange (dischi che permettono di agganciare un tubo di Venturi al resto del condotto tra le quali è normalmente inserita una guarnizione di gomma).

Il modo di montare strumenti idraulici è senza dubbio il più usato perché permette di inserire o di togliere una parte di condotto senza dover smantellare tutta la tubazione. In sezione il tubo è realizzato così:

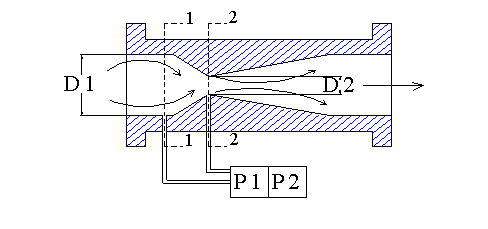fig.3

Il tubo di Venturi funziona sostanzialmente con l’equazione di Bernoulli che è:

costante

questa esprime il fatto che quando aumenta la velocità diminuisce la pressione, perché l’energia rimane costante; questa esprime che l’energia all’interno del tubo è invariata.

Se facciamo due sezioni (vedi figura) una nel punto 1 dove il fluido scorre nel condotto con la sua sezione originaria ed una sezione nel punto 2, il punto più stretto, posso scrivere:

(1)

Il tubo di Venturi è un misuratore di portata, dobbiamo trovare l’incognita . Nell’equazione compare però insieme ad altre incognite, alcune però si possono eliminare:

- rappresentano le quote del tubo nei punti 1 e 2, esse si possono cancellare perché il tubo è sempre montato in orizzontale; in questo modo i due punti hanno lo stesso baricentro dunque sono uguali.

- in quanto è una costante (deve essere tale se voglio che il tubo di Venturi funzioni correttamente. Se non è una costante, come nel caso dei gas, il dispositivo rivelerà un valore errato) da cui ottengo che:

Le pressioni le posso dedurre e quindi misurare. Per fare questo utilizzerò un manometro differenziale che misura la differenza tra le due sezioni. Avrò quindi un blocco integrale collegato con due tubi che vanno all’interno del tubo di Venturi e mi darà un valore

Ritornando all’equazione (1), voglio ricavare il valore di ed ho calcolato , mi rimane però l’incognita . Ho pertanto un’equazione con due incognite e sono così costretto a introdurre una seconda equazione detta della continuità, la quale è l’invarianza della portata in massa. Questa è:

(2)

e mi assicura che attraverso la sezione 1 passa la stessa quantità di fluido che passa attraverso alla sezione 2. Si noti che sono i diametri nei punti 1 e 2 e sono espressi al quadrato, possono quindi sostituire la aree .

Ricordando che non varia dall’equazione (2) ricavo che è:

(3)

a questo punto non resta che sostituire l’equazione (3) nella equazione (1) da cui ottengo:

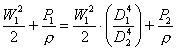(4)

ottengo così la (4) da cui ancora

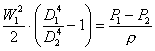(5)

risolvo la (5) sino ad ottenere

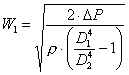(6)

nella quale noto che la differenza di pressione è proporzionale alla velocità del fluido che sta scorrendo posto sotto la radice. Il tubo di Venturi è quindi molto utile e corretto per fare misure in continuo su un condotto ma non per misurazioni simili al metodo della pesata.

I principali inconvenienti di questo dispositivo sono:

-è necessario fare la misura della pressione;

-a grosse variazioni di pressione corrispondono minime variazioni di velocità. Per questo secondo inconveniente il campo operativo (range) di questo strumento è molto limitato; si deve badare al valore di velocità da misurare, questa è una operazione piuttosto “ciappinosa”. Il tubo di Venturi è venduto per questi motivi in kit di più tubi insieme per poter scegliere quello con la strozzatura adatta a seconda della velocità del fluido che si desidera misurare.

Sorge però una domanda spontanea perché il tubo di Venturi non è strozzato come nella seguente figura?

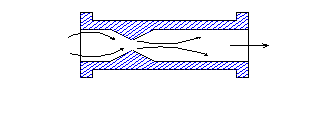fig.4

Nella figura 3 la parte convergente del tubo verso la strozzatura si restringe molto bruscamente e la parte divergente si riapre in modo dolce, se il tubo a destra della sezione 2 fosse speculare alla parte a sinistra della stessa sezione come in figura 4 si verrebbero a creare dei moti turbolenti che creano fenomeni di dissipativi con valori molto alti che possono variare tra 4 e 6 mentre in casi normali questo valore dovrebbe essere nullo per non alterare la misurazione.

Con la sezione del divergente molto allungata il fluido rimane aderente alle pareti senza creare quindi questi fenomeni dissipativi, il convergente quanto più brusco è tanto meglio funziona in questo caso infatti il fluido rimane ben attaccato alle pareti inoltre più è corto e meno saranno le perdite. Esistono comunque in vendita dei tubi di Venturi simmetrici con divergenti e convergenti entrambi molto dolci e che consentono di misurare in entrambe le direzioni.

Dobbiamo inoltre osservare che è possibile montare un terzo manometro alla fine del tubo di Venturi che ci può identificare eventuali perdite di carico tra e .

Tra queste due sezioni non vi dovrebbero essere perdite di carico tuttavia per quanto sia ben fatto il divergente ho sempre una minima perdita di carico distribuita sulla lunghezza della divergenza. Avrò quindi che e cioè la pressione nel punto di sezione 2 sarà maggiore che nel punto di sezione 1 in quanto il fluido passa nella strozzatura poi è debolmente maggiore di nel caso in cui il tubo di Venturi sia ben fatto.

Se andiamo ad analizzare un manometro differenziale (figura 5)

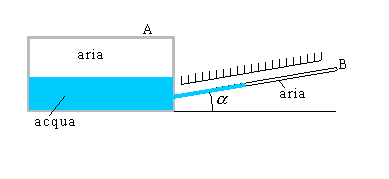fig.5

Applicando una pressione in A ed una pressione in B, ed essendo > avrò i peli liberi dell’acqua che non resteranno sullo stesso livello, ma l’acqua salirà di un certo valore lungo il tubo B (valore che posso leggere sulla scala graduata posta dietro al tubo e che è diversa a seconda dei valori che io voglio analizzare). In questo modo il dislivello , proporzionale alla differenza di pressione e . Si osservi che al posto della combinazione aria-acqua potrei avere anche due fluidi, uno più pesante e uno più leggero (per esempio mercurio-acqua).

Se quello pesante ha densità di e quello più leggero , il dislivello è proporzionale al salto di pressione secondo la relazione di Stivino, questa è una legge dell’idrostatica dei fluidi in quiete.

(7)

La lettura del diventa problematica quando assume valori nell’ordine di 1-2 mm ed è per questo motivo che serve il tubo inclinato per poter visualizzare i minimi cambiamenti. Quanto più tengo inclinato B tanto più è preciso il mio manometro differenziale; normalmente questo tubo è incernierato percui io posso variarne l’inclinazione a mio piacimento e per ogni inclinazione ho una scala di misura relativa.

Una variazione del tubo di Venturi è composta dal boccaglio e dal diaframma (figura 6), essi hanno lo stesso funzionamento; anche in questo caso ho due prese di pressione collegate al manometro differenziale e la misura è realizzata come nel caso precedente.

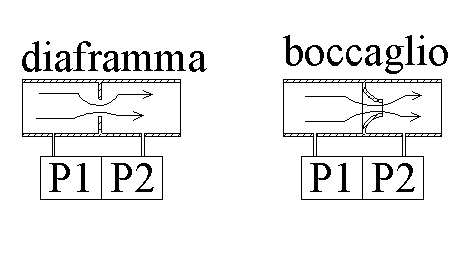fig.6

Se osserviamo la differenza di pressione vedremo che posta sotto radice quadrata essa è proporzionale alla velocità del fluido, questi strumenti introducono volutamente una forte perdita di carico localizzata che viene controllata con la seguente relazione:

(8)

dove è noto perché è scritto sul diaframma o sul boccaglio.

Se scrivo l’equazione di Bernoulli tra un punto che si trova prima del boccaglio e uno che si trova dopo avrò:

(9)

La velocità del fluido prima e dopo il boccaglio è la stessa da cui in quanto cala la pressione ma non la quantità di fluido trasportata. Per questo motivo posso eliminare il primo addendo dall’equazione (9), posso poi elidere anche il secondo addendo poiché non ho differenza di quota. La differenza di pressione l’ho misurata e lo conosco.

Da qui ricavo il valore della velocità dato da:

dove di nuovo la radice di è proporzionale alla velocità. Occorre sempre avere una serie di diaframmi per gestire tutte le possibili portate, se il diaframma ha una strozzatura troppo piccola, non va bene per portate elevate e lo stesso vele in senso contrario. E’ per questo che vengono venduti in scatole con quattro o cinque diverse strozzature.

T U B O D I P I T O T – P R A N D T L

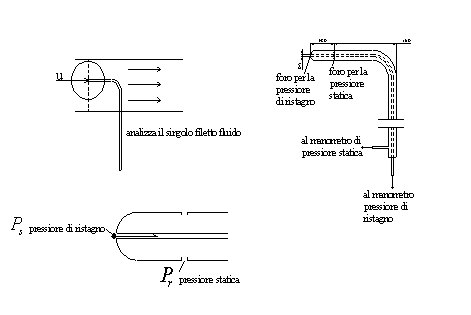fig.7

Il tubo di Pitot-Prandtl è uno strumento generalmente prodotto in acciaio inox, composto da due tubi cilindrici concentrici piegati a “L” ad un’estremità dei quali si trova un foro che consente l’ingresso di fluidi, principalmente aria, e dall’altra parte è collegato a due manometri. Questo diversamente dal tubo di Venturi è un misuratore di locale di velocità di un singolo filetto fluido e non un misuratore dell’intero condotto. Immergendo il tubo nel getto da misurare questo fluido sbatte sul “naso” del tubo stesso creando una maggiore pressione, nel punto detto anche foro per la pressione di ristagno (vedi figura 7) e la sua energia cinetica si trasforma in energia potenziale. Si notano anche due fori ai lati del tubo dove si crea una pressione statica.

Scrivendo l’equazione di Bernoulli seguendo il percorsodell’aria tra il foro di pressione di ristagno e i fori di pressione statica, si avrà:

(11)

dove si possono eliminare in quanto la velocità nel punto di ristagno è nulla, e perché i due punti sono sulla stessa retta orizzontale. Rimane pertanto il valore della velocità locale che volevo trovare

(12)

Si osservi che col tubo di Pitot è possibile effettuare solo le misure di velocità molto elevate. Per questo motivo esse è molto usato nel campo delle automobili, per esempio nella formula uno in cui si può notare un tubicino sopra al casco del pilota.

Per la misurazione di ridotte velocità esistono due tecnologie:

-la prima è basata sulle etichette cioè su dispositivi a elica che hanno l’aspetto di piccoli ventilatori. Si possono trovare di due tipi, da inserire sul condotto oppure da tenere in mano, il diametro è di circa 5-8 cm. Ad esse è collegato poi un semplice contagiri ed al numero di giri è proporzionale alla velocità del fluido.

fig.8

-la seconda tecnologia invece più scientifica adatta alle misure di laboratorio è invece l’anemometro a filo caldo. Il filo caldo è costituito da un sottile filamento (del diametro di un capello) solitamente platino che diventa incandescente per elettricità;

solitamente ha un diametro intorno al decimo di millimetro ed è lungo circa 1 cm ed è montato dentro un tubetto di protezione della lunghezza di circa 2 cm. Questo dispositivo è in pratica una sezione di tubo dentro al quale è tirato il filo caldo, l’aria passando attraverso raffreddano il filetto.

Sapendo che la potenza scambiata è proporzionale al salto di temperatura, se chiamo la potenza termica, questa è proporzionale, tramite un certo coefficiente K alla differenza di temperatura . Pertanto avrò la relazione non lineare:

(13)

dove V sono i volt, i sono gli ampere, cioè moltiplicando la tensione del filo per la corrente che passa ottengo la potenza, in cui V e i li conosco perché li posso misurare.

Il coefficiente di scambio termico K dipende dalla velocità dell’aria cioè tanto più è veloce tanto più sarà maggiore il coefficiente di scambio termico. Tale relazione è molto complicata e non sempre fornisce dei risultati precisi. Si procede generalmente per taratura dello strumento, lo si tara per tentativi anche se con lo strumento ho in dotazione tutta una curva di taratura che mi consente di verificare i risultati in cui abbiamo in funzione della velocità il K.

E’ un sistema efficace perché il sensore molto piccolo ha poca inerzia e riescie quindi a percepire ogni piccola variazione di flusso. Unico svantaggio di questo strumento è il grande prezzo e la massima delicatezza.

Oggi ne esistono esistono poi di tipo differenziale capaci di percepire il verso dello spostamento del fluido ed hanno un tempo di risposta molto breve tanto che possono essere impiegato come microfoni, l’anemometro differenziale più conosciuto è il Microflown.

Esiste poi un altro tipo di anemometro chiamato laser dopler il quale funziona a fibre ottiche. Si prende un raggio laser il quale viene scagliato contro un cristallo che lo divide in due parti perfettamente identiche tra loro; questi due raggi uguali vengono poi fatti convergere nuovamente tramite un cristallo e incrociarsi creando una X. Quando i due raggi sono in “fase” si crea l’interferenza costruttiva e la luce sarà più intensa.

Nel punto in cui si intersecano i raggi avrò quindi un’alternanza di minuscole bande bianche e nere come si può vedere in figura

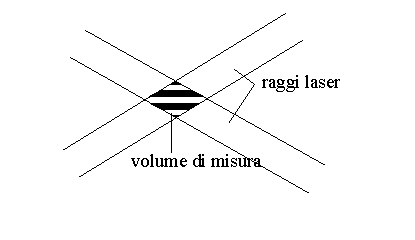fig.9

Osservando l’aria con uno strumento ottico come questo si vedono passare le impurità attraverso il volume di misura potrò quindi creare un diagramma dove in ordinata avrò l’intensità della luce I ed in ascissa il tempo T con un certo intervallo di tempo si susseguono i picchi che avranno un andamento sinusoidale crescente e decrescente poiché l’aria attraversa alternativamente aree bianche e nere, la frequenza dei picchi è proporzionale alla velocità del fluido.

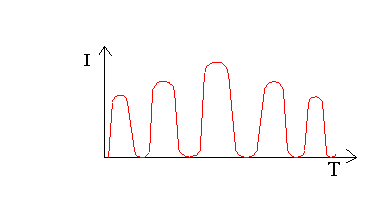fig.10

A P P L I C A Z I O N I

Dopo aver visto in modo teorica il funzionamento di questi strumenti possiamo ricercare degli esempi pratici. Un tipico esempio del tubo di Venturi è il carburatore (per altro non più utilizzato sulle attuali autovetture). Questo pezzo serve a miscelare l’aria con la benzina ed è fatto nel modo seguente:

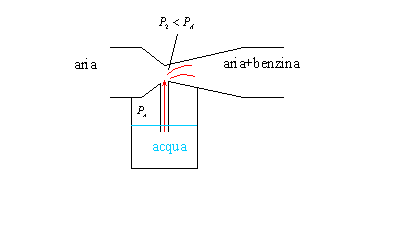fig.11

Come si può vedere in figura la pressione della strozzatura è minore di quella atmosferica quindi il tubo di Venturi funziona come un aspiratore di fluido; si noti che la forza aspirante è proporzionale alla velocità e quindi alla portata della benzina, questo comporta il fatto che vi è un rapporto aria-benzina sempre costante.

Un’altra applicazione del tubo di Venturi è la vecchia polpetta per il DDT, tirando la leva e poi spingendola in avanti si creava un risucchio di aria che aspirava la quantità utile di prodotto e che lo mischiava con l’aria.

Venendo al caso del tubo di Pitot, possiamo parlare di uno strumento chiamato piezometro; esso viene utilizzato per misurare la pressione nei condotti. Avendo un serbatoio collegato con un condotto ad una abitazione ho un tubo verticale (il piezometro) collegato a questo condotto nel quale l’acqua che va dal serbatoio alla casa risale di un certo livello, questo è detto piezometro statico; accanto a questo troviamo un secondo piezometro che invece di fermarsi sul tubo entra in esso con una specie di punta simile al tubo di Pitot in cui l’acqua sbatte creando una pressione maggiore, questo è detto piezometro dinamico. Misurando l’altezza dell’acqua nel piezometro avrò il cosiddetto carico piezometrico e ad ogni valore di carico corrisponde un determinato valore in termini di pressione (ad esempio con 50 m di carico piezometrico ho 5 bar di pressione). Posso anche identificare le perdite di carico misurando la distanza tra il pelo dell’acqua ed il livello del terreno.

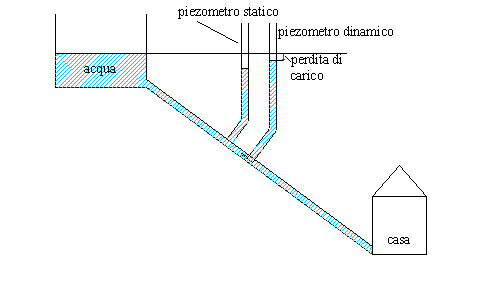fig.12