ESERCIZIO NUMERICO _ Relativo al CICLO CLASSICO FRIGORIFERO (miscele d’acqua e vapor d’acqua)

v CONOSCENZE PRELIMINARI:

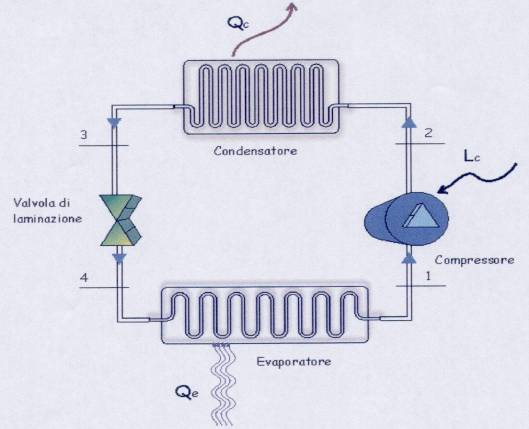
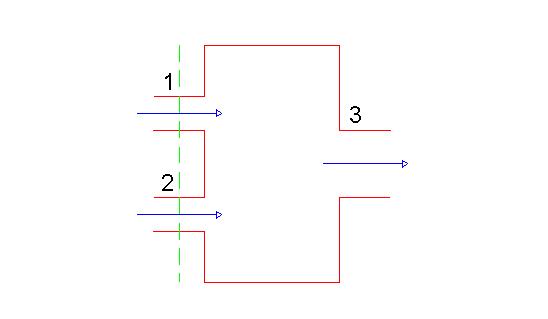
La macchina frigorifera è composta da quattro sistemi aperti che, collegati tra loro, generano un sistema chiuso.

• COMPRESSORE: macchina che opera una compressione adiabatica del liquido e necessita di una certa energia esterna (lavoro Lc) per poter funzionare (questo azionamento è generalmente effettuato tramite motori elettrici).

L’energia spesa dal compressore si trasferisce nel gas evolvente che si surriscalda rispetto alla temperatura di saturazione aumentando anche la sua pressione.

• CONDENSATORE: macchina che compie una trasformazione isobara del liquido che viene raffreddato.

Il refrigerante, mantenendo costante la pressione, si condensa totalmente passando dallo stato gassoso a quello liquido ed essendo stato raffreddato rilascia una certa quantità di calore ( Qe ).

• VALVOLA DI LAMINAZIONE: può essere costituita da una valvola (valvola di strozzatura, come nel caso del seguente esercizio) oppure da un tubo di piccolo diametro (tubo capillare).

Questa valvola permette al liquido refrigerante di effettuare una espansione isoentalpica, considerata irreversibile anche nei cicli ideali.

· EVAPORATORE: macchina che opera una vaporizzazione del liquido che passa dallo stato liquido a quello gassoso.

Questa operazione è isoterma e isobara e il refrigerante assorbe una grande quantità di calore dall’ambiente esterno, raffreddandolo.

In definitiva la macchina frigorifera ha il compito di trasformare l’energia entrante sotto forma di lavoro ( Lc ) in assorbimento di calore uscente ( Qe ).

Quindi possiamo dire che la sua efficienza sarà più alta se, con il minor lavoro possibile, produce una maggiore quantità di calore sottratto. Questa è determinata dal rapporto tra ciò che “esce” e ciò che “entra”.

Calore sottratto al serbatoio freddo

w = ———————————

Lavoro compiuto sul refrigerante

ESERCIZIO

Dati: Determinare:

P₁= 3,6 bar Coefficiente economico (w)

P₂= 9,6 bar

Liquido refrigerante: FREON R12

N.B.:il Freon R12, a causa di problematiche ambientali, è considerato fuori legge; oggi si preferisce utilizzare liquidi diversi con caratteristiche simili.

T 2 1 1 1 4 3 S T
50	3
40
5
		S

Sul diagramma T.S. del Freon R12 possiamo vedere cosa accade ai vari passaggi:

· 1-2 : il compressore opera una compressione adiabatica reversibile (ad entropia costante).

Nel grafico: si sale in verticale partendo dal punto 1 fino ad arrivare al punto 2.

· 2-3 : il condensatore compie una trasformazione isobara (a pressione costante) del refrigerante che viene raffreddato e passa allo stato liquido.

Nel grafico: al di fuori della campana avremo un comportamento caratteristico di una isobara che diventa orizzontale all’interno della campana (condensazione completa fino alla curva limite inferiore).

· 3-4 : la valvola strozzatrice opera una trasformazione irreversibile con aumento di entropia e diminuzione di pressione.

Nel grafico: attraverso un segmento verticale si passa dal punto 3 al punto 4 (fino alla pressione del ramo inferiore).

· 4-1 : l’evaporatore opera una vaporizzazione; viene sottratto calore dall’interno della cella frigorifera e viene dato al fluido.

Nel grafico: attraverso un segmento orizzontale si passa dal punto 4 al punto 1.

Attraverso la struttura del ciclo e il diagramma del Freon R12 è possibile

ricavare punto per punto i valori delle pressioni e delle entalpie specifiche del fluido.

Sistemiamo i dati così ricavati in una tabella:

	PRESSIONE (bar)	TEMPERATURA (°C)	ENTALPIA SPECIFICA (Kj / Kg)
Punto 1	3,6	5	353,611
Punto 2	9,6	50	371,07
Punto 3	9,6	40	288,53
Punto 4	3,6	5	238,52

Tab. dei valori energetici specifici del fluido nei vari punti del ciclo.

Determinare il rendimento frigorifero.

Poiché sappiamo che:

calore sottratto dall’evaporatore

ωf = —————————————

lavoro speso dal dompressore

ω = ˙Qe / ˙Lp = Qe / Lp

con

˙Qe , ˙Lp termini di potenza;

Qe , Lp termini di energia specifica.

Equazione per il sistema aperto per l’evaporatore:

Qe = h₁-h₄ = 115,085 Kj / Kg

Equazione per il sistema aperto per il compressore:

Lp = h₂-h₁ = 17,459 Kj / Kg

Quindi per ricavare il rendimento di questo ciclo frigorifero:

ωf = Qe / Lp = 6,6 (valore decisamente alto).

Consideriamo ora il rendimento della macchina di CARNOT ideale:

prendiamo come temperatura massima quella di evaporazione e come temperatura minima quella di condensazione.

Mc = Tev / ( Tcon. – Tev. ) = 278 (K) / 35 = 7,9

· CONSIDERAZIONE:

La macchina da noi considerata introduce un ciclo frigorifero differente da quello di Carnot e, come abbiamo potuto rilevare dall’esercizio svolto, ha un rendimento inferiore a quello che avrebbe la macchina ideale di Carnot.

COMFORT TERMO – IGROMETRICO (ovvero quale deve essere la condizione dell’ambiente per avere una situazione di piacevolezza dal punto di vista fisico)

Possiamo avere vari tipi di comfort che generano una situazione piacevole all’interno di un ambiente:

• Termo-igrometrico (termodinamica);
• Visivo (illuminotecnica);

• Acustico (acustica applicata);
• Vibrazionale (meccanica applicata);

• Olfattivo (termofluidodinamica);
• Tattile (legata al design).

Quello da noi preso in considerazione è il comfort termoigrometrico che coinvolge e lega tra loro due grandezze fondamentali per l’abitabilità dell’ambiente:

· TEMPERATURA;

· UMIDITA’.

Es. Sauna o bagno turco: sebbene la temperatura non sia molto elevata, la sensazione non è piacevole a causa dell’elevata umidità.

Es. Mare: possiamo trovare la stessa temperatura della sauna ma il grado di umidità è molto inferiore quindi il risultato è un clima confortevole.

Inoltre nella progettazione degli impianti di condizionamento di un locale non è possibile decidere in assoluto una temperatura e un grado di umidità ma vanno presi in considerazione anche altri fattori quali:

· Destinazione d’uso del locale;

· Età delle persone che lo frequentano;

· Tipo di abbigliamento previsto.

Es. Palestra: facendo attività fisica il corpo produce calore quindi la temperatura del locale può essere inferiore e la sensazione è ugualmente piacevole.

Es. Ospedale: questo luogo ospita persone debilitate, malate e, per lo più, inattive quindi la temperatura deve essere maggiore.

Il concetto di comfort non è standard ma soggettivo; la differenza tra persona e persona è evidente anche all’interno un gruppo di individui che abitano ad una certa latitudine e longitudine quindi non si avrà mai il comfort totale.

In questo campo sono state fatte diverse sperimentazioni significative tra cui ricordiamo quella di Fanger .

· FANGER: scienziato di Copenaghen che fece esperimenti sulle condizioni climatiche ricreando precise condizioni ambientali di caldo e freddo.

Utilizzando studenti come tester stabilì la temperatura ottimale di un ambiente in relazione all’attività d’uso e alle persone che lo frequentavano (tenendo conto anche dell’abbigliamento: variabile legata ad usi e costumi della popolazione).

Il metodo sperimentale di Fanger consiste nell’accogliere un numero di studenti in una stanza e assegnare loro diverse attività da svolgere con condizioni ambientali differenti e registrare infine la valutazione da loro assegnata riguardo al grado di comfort.

-1 0 1

FREDDO

COMFORT

CALDO

PMV: voto medio previsto

Se –0,5 < PMV < 0,5 si verifica una situazione di scostamento normalizzata rispetto alle condizioni di comfort.

Meno del 10% dei soggetti è insoddisfatto

│PMV│< 0,5 questa diventa la condizione di progetto poiché le condizioni poste si sono rivelate adatte a creare un ambiente ospitale.

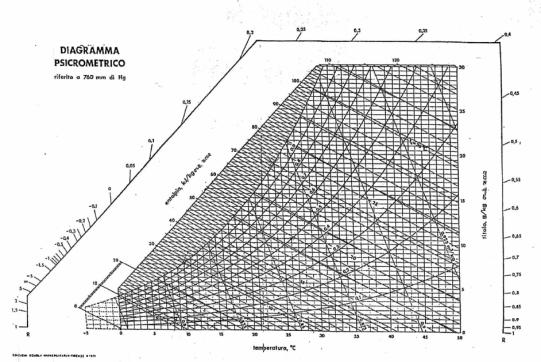
Un’altra sperimentazione interessante è quella fatta da ASHRAE che studia le condizioni di comfort ottimali basandosi su diagrammi per condizioni reali.

Questo metodo prende in considerazione condizioni medie, di moderato vestimento e media attività ma può comunque essere utilizzato per condizioni più estreme.

Esistono molte tabelle empiriche ricavate in base a teorie più o meno efficaci e soprattutto in base a rilievi sperimentali, ovvero testate su varie persone, che permettono di decidere quali devono essere gli intervalli di temperatura e di umidità entro cui bisogna rimanere per mantenere il locale vivibile e piacevole.

Queste tabelle si basano soprattutto su una teoria che considera il corpo umano come un sistema aperto, quindi un sistema che scambia calore con l’esterno.

Partendo da questi presupposti possiamo scrivere:

EQUAZIONE DEL BILANCIO ENERGETICO DEL CORPO UMANO:

∑ Mi ( lci + lpi + hi ) = Q – L

con:

Mi = portata in massa;

Q = potenza termica;

L = potenza meccanica.

Inoltre lo studioso DU BOIS mette in relazione la superficie del corpo umano con gli scambi termici all’interno di questo sostenendo che ad una maggior superficie corporea corrisponde una agevolazione negli scambi termici ed arrivando a formulare la seguente relazione empirica e dimensionalmente non omogenea:

A = 0,202 m^0,425 h^0,725 = 1,8 m²

Con:

m = massa (es. 70 kg)

h = altezza (es. 1.70 m)

Pertanto da queste ipotesi si può arrivare a scrivere l’equazione energetica del corpo umano che, essendo un sistema aperto, scambia calore ed energia con l’esterno ed esso stesso ne produce. Tale relazione esprime inoltre una condizione di equilibrio poiché il calore perso equivale al calore ricevuto:

M – Lp – Lg – U – Ed – Es – Er – Vs = R + C

Con:

M = somma di tutte le energie prodotte dall’organismo.

E’ positiva perché prodotta interamente dal corpo attraverso l’assunzione di

cibo (reazioni di combustione dei carboidrati). Si misura un watt.

Lp = energia utilizzata per l’attività polmonare; pompa alternativa che cede energia meccanica nell’aria e che viene dissipata negli attriti.

Lg = lavoro muscolare fatto contro le forze di gravità e tutte le forze esistenti; è detto meccanismo dell’erogazione.

U = energia di accumulo. E’ negativa perché l’organismo, in caso di necessità, produce energie in eccesso e viene accumulato calore che aumenta la temperatura corporea media (36,5°/37°).

Ed = dissipazione legata alla pelle asciutta: evaporazione sulla pelle che richiede calore latente di vaporizzazione. E’un termine fisso che identifica un processo naturale (prima fase).

Es = sudore in fase umida: è il calore disperso per evaporazione del sudore sulla superficie della pelle (seconda fase).

Ed – Es = Ws : termine fondamentale che identifica la quantità di calore che l’organismo scambia con l’esterno attraverso la sudorazione.

Er = energia legata al vapore di H₂O emesso con la respirazione.

Vs = ventilazione polmonare : Vs = Mv Cpa (Tout – Tin)

Con Tout – Tin = incremento di temperatura.

Er – Vs = calore disperso con la respirazione.

R + C = dispersione complessiva dello scambio termico.

Questo scambio termico può avvenire per:

- conduzione;

- convezione ( C ) : scambio mediato da un gas;

- irraggiamento ( R ).

	M

La sensazione di comfort è all’interno di una determinata fascia di scambio termico; se il corpo disattiva tutti i meccanismi di sudorazione perché l’ambiente è troppo freddo, quindi cerca di minimizzare gli scambi con l’esterno, la sensazione che si riceve è quella di freddo.

Al contrario, se l’ambiente è molto caldo, il corpo aumenta la sudorazione quindi lo scambio con l’esterno e la sensazione che si riceve quella di caldo.

Il nostro dispositivo interno di regolazione è la sudorazione. Se l’ambiente esterno è saturo il sudore non può evaporare perché l’aria è già piena di tutto il vapor d’acqua disponibile e quindi, essendo ostacolato il meccanismo di regolazione, aumenterà la sudorazione.

Es. Sauna: umidità quasi al 100% (condizione di saturazione dell’aria). Il corpo mette in azione il meccanismo della sudorazione ma, non potendo evaporare, non riesce trarne refrigerio quindi la sensazione è sempre più di caldo.

Es. Ambiente secco e areato: la sudorazione è favorita perché appena si forma il sudore viene subito asportato e più facilmente evaporato. La sensazione che si ricava è dunque di freddo.

Consideriamo ora il DIAGRAMMA PSICROMETRICO:

Il diagramma psicrometrico lega insieme titolo (grandezza che identifica l’umidità) e temperatura.

Le rette trasversali sono rette a comfort costante; a umidità inferiore la sensazione che si avverte è uguale anche se aumenta la temperatura.

Es. Ambiente caldo secco (mare): la sensazione che si prova è molto simile a quella in un ambiente molto più freddo ma umido.

Inoltre, se consideriamo il grafico diviso da queste rette in tre parti uguali, possiamo dire che all’estremità destra la sensazione è di estremo freddo; al centro la sensazione è sostanzialmente di benessere; all’estremità sinistra (in alto) la sensazione è di estremo caldo. Nelle due situazioni estreme le funzioni vitali non sono garantite.

Riassumendo:

Il parametro per valutare il comfort dell’ambiente è il comfort termo-igrometrico ovvero in funzione dell’ambiente, dell’attività a cui è destinato e dei frequentatori (anziani, giovani, malati, atleti,…) esistono tabelle in cui sono consigliati intervalli di temperatura e di umidità, legati in modo che si possa aumentare o l’uno o l’altro in funzione dell’ambiente preso in considerazione, all’interno dei quali l’abitabilità è sufficientemente buona (da considerare la variabilità soggettiva).

v Accenno alla MASSIMA CAPACITA’ TERMICA DELL’UOMO (in condizioni estreme di caldo o di freddo):

La massima dose di energia che il corpo umano può scambiare con l’esterno in caso di caldo o freddo è: 600 kj.

In queste situazioni estreme l’organismo “spegne” la digestione, la circolazione del sangue negli arti, riduce le difese immunitarie, annulla cioè tutte le funzioni secondarie per cercare di conservare gli organi interni e il cervello.

L’ipotalamo è il centro regolatore dove si trovano questi sensori; ci sono però alcuni casi in cui può essere ingannato a tal punto che l’organismo inizia a disattivare le funzioni secondarie senza che vi sia realmente bisogno.

Es. un uomo che prende il sole per lungo tempo, in una situazione di estremo caldo, è prossimo a 600 kj; nel momento in cui entra in acqua la differenza di temperatura è tale che l’ipotalamo subisce un raffreddamento istantaneo e inizia a spegnere tutte le funzioni secondarie e, in casi estremi, può esserci anche un blocco respiratorio.

ESERCIZIO NUMERICO _ Relativo ad EMISSIONI D’ARIA e VAPOR ACQUEO

v CONOSCENZE PRELIMINARI:

Mv

TITOLO : X = –––– ( kg_v / kg_a ) ed esprime il rapporto tra massa d’aria e vapore.

Ma

Mvs: massa di vapore di saturazione.

Data una massa di vapore Va esiste una particolare Mvs in grado di saturarla; un ulteriore apporto d’acqua non evapora oppure si condensa sulle pareti, ritornando liquido. All’aumento di temperatura serve più vapore di saturazione e viceversa. Per T « 0 diminuisce ma non è mai nullo; si annulla solo allo 0 kelvin mentre per T vicine a 100°C tende a ∞.

T

Vs

100

0

PRESSIONI PARZIALI:

Vv nv Mv / μv

Pv = Ptot —— = Ptot —— = Ptot ————————

Vtot ntot Mv / μv + Ma / μa

Va na Ma / μa

Pa = Ptot —— = Ptot —— = Ptot ————————

Vtot ntot Mv / μv + Ma / μ

Con:

μa = 29 kg / kmol

μv = 18 kg / kmol

UMIDITA’ RELATIVA (o grado idrometrico):

per umidità relativa si intende il rapporto tra masse mentre per grado idrometrico il rapporto tra pressioni.

Mv Pv

Φ = —— ≈ ——

Mvs Pvs

Equazione che lega titolo e grado igrometerico:

φ Pvs

X = 0,622 ——————

Ptot – φ Pvs

ESERCIZIO

Dati: Determinare:

Aria umida a T= 30°C Titolo: X

φ= 0,6 (60%) Pv: pressione parziale del

P= 1 BAR (pressione dell’ambiente) vapore

Situazione climatica estiva della Pianura Padana.

Dalla definizione di umidità relativa o di grado idrometrico si ha:

Mv massa vapore μv n. moli vapore

Φ = —— ( ————————— ) = —— ( ————————— )

Mvs massa vapore saturo μvs n. moli vapore saturo

Poiché il vapor d’aria e il vapor d’acqua sono assimilabili ad un gas perfetto possiamo scrivere l’equazione dei gas perfetti:

Pv V = μv R₀ T

Con:

Pv = pressione vapore;

V = volume;

μv = numero di moli del vapore;

R₀ = costante universale dei gas;

T = temperatura assoluta.

In situazioni di saturazione, l’equazione diventa:

Pvs V = μvs R₀ T

Pv

Φ = ——

Pvs

Da cui ricaviamo:

Pv = φ Pvs = 0,6 0,04241 = 2545 Pascal

Dobbiamo ora ricavare il titolo assoluto.

Sappiamo che:

Mv massa volume μv nv

X = —— ( —————— ) = ————

Ma massa aria μa na

E che μv e μa sono noti quindi il loro rapporto è costante e vale sempre 0,622; possiamo quindi riscrivere la formula in questi termini:

Pv φ Pvs

0,622 ———— = 0,622 ——————

Ptot – Pv Ptot – φ Pvs

In valori numerici:

0,025446

0,622 —————— = 0,0162

1 – 0,025446

g (di vapore)

che equivale a 16,24 —————

kg (d’aria)

ESERCIZIO NUMERICO _ Relativo alle MISCELAZIONI

Abbiamo due flussi d’aria in entrata in condizioni differenti; avverrà una semplice miscelazione quindi senza scambio né di calore né di umidità. Vogliamo determinare i valori del flusso d’aria in uscita.

Es. Ambiente caldo secco (mare): la sensazione che si prova è molto simile a quella in un ambiente molto più freddo ma umido.

Dati: Determinare:

P= 1 BAR Titolo: X₃

1° corrente: portata in massa d’aria: 400 kg / h T₃

2° corrente: portata in massa d’aria: 800 kg / h J₃

T₁= 32°C Φ₃

T₂= 26°C

Φ₁= 0,8 (80%)

Φ₂= 0,5 (50%)

Considerando il bilancio interno di energia quindi, con la legge di conservazione della massa (massa d’aria, massa d’acqua, massa totale), si riescono a definire le varie grandezze in ingresso e in uscita.

Dal bilancio è evidente che la portata in massa in 3 è uguale alla somma delle portate in massa in 1 e 2.

Quindi:

. . .

M_3a = M_1a + M_2a = (400 + 800) kg_a / h = 0,33 kg_a / s

Possiamo riscrivere la medesima equazione per il bilancio in massa per il vapore d’acqua poiché sappiamo che l’acqua entrerà e uscirà sempre sotto forma di vapore, senza subire cambiamenti di stato.

Quindi:

. . .

M_3v = M_1v + M_2v

Dobbiamo però ricavare i valori del vapore in ingresso; dalla definizione di titolo si ha:

M_v

X = —— (sia in termini specifici che in termini orari)

M_a

Quindi:

. .

M_v = X M_a

Riscrivendo l’equazione:

. . .

X₃ M_3a = X₂ M_2a + X₁ M_1a

Sappiamo inoltre che:

φ Pvs (t)

X = 0,622 —————

P – φ Pvs

Quindi :

0,8 0,4753

X₁ = 0,622 –––––––––——— = 0,0245 kg_v / kg_a = 24,5 g_v / kg_a

1 – 0,8 0,475

Analogamente ricaviamo :

X₂ = 10,6 g_v / kg_a

Sappiamo che M1a, M2a, M3a, X1, X2 sono noti, quindi, utilizzando l’equazione sulla conservazione della portata in massa del vapore, possiamo ricavare:

. .

X₂ M_2a + X₁ M_1a

X₃ =————.—————— = 15,23 g_v / kg_a

M_3a

Inoltre sappiamo che l’entalpia specifica non cambia quindi possiamo ricondurci all’equazione scritta in termini di entalpia specifica per kg di aria secca:

flusso di entalpia in uscita = flusso di entalpia in entrata.

Con:

flusso in entrata = rapporto tra portate in massa dell’aria per entalpia specifica.

flusso in uscita = rapporto tra portate in massa dell’aria secca per entalpia specifica

della miscela su 1 kg d’aria secca.

4h – Q L = 0 entalpia = 0

. . .

M_3a J₃ = M_1a J₁ + M_2a J₂

Si ricava:

. .

M_1a J₁ + M_2a J₂

J₃ = ————.———————

M_3a

Per ricavare J₁ e J₂ è sufficiente applicare la formula:

J₁ = [ T₁ + X₁ (2500 + 1,9 T₁)] kj / kg_a

Sostituendo i valori:

J₁ = 32 + 0,0245 2500 + 1,9 32 = 94,7 kj / kg_a

Analogamente:

J₂ = 26 + 0,0106 (2500 + 1,9 26) = 53 kj / kg_a

400 94,7 + 800 53

J₃ = —————————— = 66,9 kj / kg_a

1200

Dobbiamo ora ricavare il valore di T₃:

J₃ = [ T₃ + X₃ (2500 + 1,9 T₃) ] kj / kg_a

Dall’equazione ricaviamo T₃:

J₃ – 2500 0,01523

T₃ = —————————

1 + 1,9 X₃

Sostituendo ottengo:

66,9 – 2500 0,01523

—————————— = 28°C

1 + 1,9 0,01523

Ricaviamo infine il valore di umidità relativa (φ₃):

φ₃ Ps₃

X₃ = 0,622 ——————

P – Ps₃ φ₃

(dalle tabelle ricavo che Ps₃ = 0,03778 Bar);

quindi:

P X₃ 1 0,01523

φ₃ = ———————— = ——————————— = 63%

Ps₃ (X₃ + 0,622) 0,03778 (0,01523 + 0,622)

Il problema si può risolvere facilmente anche per via grafica riferendosi al diagramma psicrometrico:

le curve rappresentate identificano situazioni a umidità relativa costante; quindi note le temperature e i gradi idrometrici (umidità relativa) dei punti 1 e 2 è possibile determinare il punto 3 in quanto è la media pesata in funzione delle portate in massa dei titoli e quindi anche delle temperature.

Per un controllo sui valori trovati è comunque bene rappresentare sul diagramma le due situazioni termodinamiche all’ingresso dei due condotti e ricavare con i dati (formule e calcoli) la situazione in uscita: questa deve risultare necessariamente in un punto del segmento congiungente 1i due punti in ingresso.