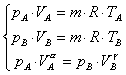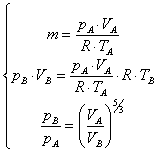Variabili termodinamiche ed equazioni di stato
Le variabili che descrivono un sistema termodinamico, dette variabili termodinamiche, sono: pressione (p), temperatura (T), volume (V), quantità di materia (o massa) espressa in numero di moli (n).
Le variabili P, T, V, e n non sono fra loro indipendenti; le relazioni che le legano sono dette equazioni di stato.
Per i gas tali relazioni ci vengono dalla proprietà generale che definisce la temperatura come una costante di proporzionalità moltiplicata per pressione e volume, e divisa per la massa:
![]() (1)
(1)
Consideriamo ora il caso più specifico di quei gas, di natura estremamente rarefatta, detti gas ideali.
Quest’ultimi soddisfano la legge di Boyle, ricavata nel 1662 dal chimico Robert Boyle, secondo cui in un gas a bassa densità, mantenuto a temperatura costante, il prodotto della pressione p per il volume V, diviso per il numero di moli n, è una costante:
A T costante: ![]() costante. (2)
costante. (2)
Ricordando
la (1), proprietà generale valida per
ogni gas, e dimostrando sperimentalmente che nei gas ideali la costante di
proporzionalità k è sempre uguale, possiamo facilmente dedurre l’equazione di stato dei gas ideali
detta legge
dei gas ideali:
PV = nRT (3)
I
in cui R è detta costante universale dei gas. Si ricava sperimentalmente il suo valore:
![]()
Trasformazioni dei gas
In un sistema termodinamico, al mutare delle variabili termodinamiche, si attuano trasformazioni o processi termodinamici che ne alterano lo stato.
Per quanto concerne i gas ideali, i valori di temperatura, volume e pressione variano secondo le limitazioni imposte dalla loro equazione di stato (3).
Per verificare sperimentalmente queste relazioni consideriamo una certa quantità di gas racchiusa in un cilindro dotato di pistone mobile.
Possiamo facilmente rappresentare i risultati ottenuti in grafici in cui una variabile è scritta in funzione dell’altra.
In particolare notiamo l’esistenza di quattro diversi tipi di trasformazione:
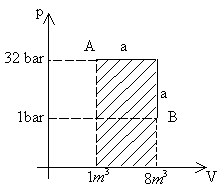
a. Isobara. Si ottiene mantenendo costante la pressione e variando temperatura e volume, i quali risultano essere direttamente proporzionali tra loro. Nel nostro cilindro otteniamo questo risultato scaldando la base conduttrice e movendo il pistone.
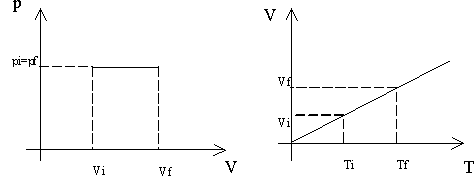
Fig. 1
b. Isocora. Si ottiene mantenendo costante il volume, e variando temperatura e pressione. Anche in questo caso si riscontra un rapporto di diretta proporzionalità tra le variabili
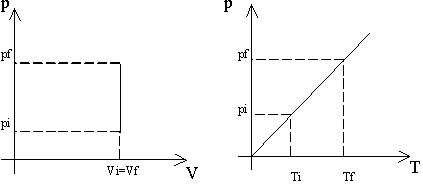
Fig. 2
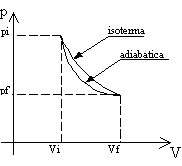
c. Isoterma. Si ottiene mantenendo costante la temperatura e variando pressione e volume. Contrariamente, in questo caso, le variabili vengono a legarsi in un rapporto d’indiretta proporzionalità. L’equazione che esprime questa relazione per i gas ideali non è altro che la già osservata legge di Boyle (1).
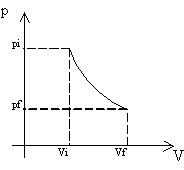
Fig. 3
d. Adiabatica. Si ottiene eliminando il flusso di calore nel sistema. Per permettere questa trasformazione è necessario che il nostro contenitore cilindrico sia termicamente isolato dall’ambiente esterno. Supponiamo, per esempio, di ricoprirlo con polistirolo espanso.

Fig. 4
Energia termodinamica, flusso di calore ed equivalente
meccanico del calore
Parlando di trasformazioni adiabatiche si è introdotta la nozione di flusso di calore. Questo concetto è facilmente intuibile considerando un sistema termodinamico alla cui variazione di temperatura trova riscontro l’alterazione termica di un sistema vicino.
Fino alla metà del XIX secolo si credeva che, responsabile di tale interazione tra sistemi termodinamici, fosse un fluido, detto calorico, o più semplicemente calore. Si pensava che tale sostanza potesse fluire dentro o fuori dal sistema stesso e, tanta ne usciva (o entrava) dall’ambiente circostante il sistema, tanta ne entrava (o usciva) nel sistema stesso.
Oggi sappiamo che questa teoria è errata e che la ragione di tali interazioni è da ricercarsi nel concetto d’energia interna o energia termodinamica.
Questa nozione ci dice, infatti, che un sistema trasferisce la sua energia interna (termodinamica) cambiando la temperatura (o la fase) di un altro sistema, oppure usando la sua energia interna per compiere un lavoro meccanico.
Importantissima, quest’ultima proposizione, rende esplicita quell’uguaglianza tra energia (termodinamica) e lavoro già osservata per l’energia cinetica e per quella potenziale.
In altre parole dice che il flusso di calore entrante, e/o il lavoro meccanico fatto sul sistema, possono contribuire entrambi ad innalzare la temperatura del sistema termodinamico.
Si giunse a questa conclusione già nella prima metà del XIX secolo; in particolare furono determinanti le osservazioni del Conte Rumford e i famosi esperimenti di Joule.
Tale equivalenza è espressa dalla formula:
![]() (4)
(4)
Questo risultato, noto come equivalente meccanico del calore, è
traducibile in una relazione fra l’unità di misura del lavoro nel SI, il joule (J), e l’unita di flusso di calore, la
caloria (cal):
1cal = 4.185 J
Volendo invece trovare un
legame quantitativo esistente tra flusso di calore e variazione di temperatura
si deve introdurre la nozione di capacità
termica (C).
Si dimostra che un flusso
infinitesimo di calore (dQ) in un sistema termodinamico provoca una
variazione di temperatura infinitesima (dT), con una costante di
proporzionalità (C):
![]() (8)
(8)
Poiché Adx = dV (variazione infinitesima del volume del gas), possiamo
riscrivere l’equazione:
dL = p dV (9)
L’Eq. (8) è specifica di un moto rettilineo del pistone in base alla
geometria del contenitore; la (9) è invece una forma più generale che
vale quando un gas varia il suo volume spingendo in ogni direzione verso
l’esterno.
Essendo nell’Eq. (9)
la pressione p funzione di V e T, come per il flusso di calore, non potremo
semplicemente integrare l’equazione; per ottenere il lavoro dovremo, infatti,
specificare prima in che modo si è avuta la variazione finita di volume.
Dall’Eq (9) ricavo l’integrale che esprime il lavoro
fatto nell’andare dallo stato 1 allo stato 2, rispetto ad una variazione
infinitesima di volume:
![]() (10)
(10)
Quest’integrale è definito
solo se si precisa il cammino da 1 a 2.
Se il cammino è tracciato in
un diagramma p-V il
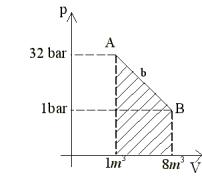
lavoro fatto dal gas ha un’interpretazione immediata: è l’area sottesa alla
curva di p in funzione
di V.
Se il volume ![]() è maggiore di
è maggiore di ![]() , il gas espande e il lavoro fatto è positivo, al contrario,
se
, il gas espande e il lavoro fatto è positivo, al contrario,
se ![]() è minore di
è minore di ![]() , il gas viene compresso e il lavoro fatto dal gas è
negativo.
, il gas viene compresso e il lavoro fatto dal gas è
negativo.
Se pensiamo al lavoro fatto
da un sistema termodinamico come all’area sottesa dalla curva di p in funzione
di V, diventa evidente che il lavoro debba dipendere dal cammino seguito
durante la trasformazione.
Andiamo allora a vedere,
rispetto alle trasformazioni definite prima, il contributo del lavoro.
a. Isobara. Dall’Eq. (9) si ricava facilmente che, per una trasformazione a
pressione costante, il lavoro fatto dal gas equivale al prodotto tra il valore
costante di pressione e la variazione di volume.
Generalmente, se il volume di un gas
deve aumentare senza variazioni di
pressione, la temperatura deve aumentare.
Calcoliamo pertanto la variazione di temperatura per un gas
ideale.
Supponiamo che temperatura, pressione e
volume iniziali siano T,P e V, e che V aumenti di dV mentre p rimane
costante. Dalla legge dei gas ideali, T = pV/nR, segue che
a p costante: ![]() (11)
(11)
Sostituendo p/nR con T/V, la (11) diventa
Come già accennato, le variazioni d’energia interna (U) di un sistema termodinamico possono essere dovute o ad un suo trasferimento, che si manifesta alterando la temperatura di un altro sistema, o ad un suo utilizzo in un lavoro meccanico sull’ambiente circostante.
Non essendo possibile, in una trasformazione adiabatica, alcun contatto termico e quindi flusso di calore del sistema con l’esterno, le possibili variazioni d’energia interna si riducono al solo caso del lavoro meccanico.
Fig. 5
Fig. 6
Fig. 7
Fig. 8