Dall’Olio Federica - matr. 138888

LE PERDITE DI CARICO

Argomenti trattati:

- Introduzione

- Perdite di carico distribuite

- Diagramma di Moody

- Perdite di carico concentrate

- Lunghezza equivalente

- Problemi e risoluzioni

Introduzione

Per comprendere al meglio il concetto di perdite di carico è bene ricordare il teorema di Bernoulli che permette di trovare relazioni che legano le proprietà dei fluidi in diverse sezioni di un condotto. Tale teorema è definito dalla seguente relazione:

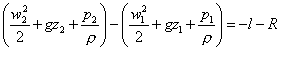dove w = velocità, g = costante gravitazionale, p = pressione, r = densità, l = lavoro, R = resistenza, z = quote piezometriche.

Con la precedente relazione Bernoulli ci dimostra che è possibile parlare di conservazione dell’energia per i fluidi senza però trascurare il valore della resistenza e quello degli scambi di energia con l’esterno.

E’ proprio il valore della resistenza che prenderò in considerazione e che andrò ad analizzare in questa tesina.

Per prima cosa bisogna distinguere le perdite di carico in due diversi tipi: quelle distribuite e quelle concentrate ( o localizzate ).

Andiamo ad analizzarle con più attenzione.

Perdite di carico distribuite

Per perdite di carico distribuite si intende il lavoro svolto da un fluido per percorrere un certo tratto di tubo a sezione costante e uniforme; per tanto tale lavoro sarà in funzione esclusivamente del diametro del tubo, della scabrezza del tubo e del numero di Reynolds.

Per quanto riguarda la scabrosità del tubo mi soffermo per alcune considerazioni: il tubo che si prende in considerazione non è mai da pensare ideale, la sua superficie infatti presenterà sempre determinate irregolarità.

Per calcolare il valore preciso delle perdite di carico distribuite basta applicare la seguente formula:

dove l è definito come coefficiente d’attrito e si calcolerà differentemente a seconda del moto del fluido.

Diagramma di Moody

Tramite la precedente relazione si è potuto costruire il seguente grafico:

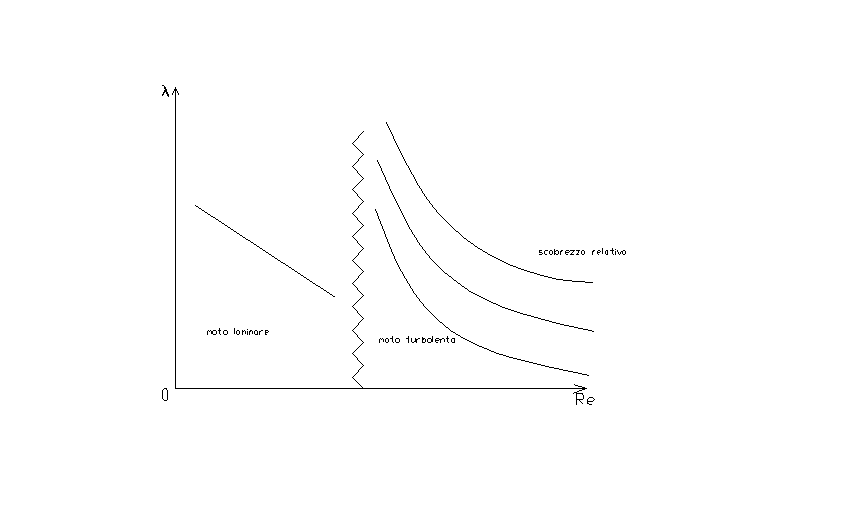
In questo abaco possiamo notare tre distinte zone in cui i fluidi adottano comportamenti diversi:

· Zona caratterizzata dal moto laminare

· Zona di transizione in cui il comportamento del fluido è incerto

· Zona caratterizzata dal moto turbolento

Nella zona a moto laminare ( la meno comune) le perdite sono inferiori. La scabrezza non incide sul cambiamento delle perdite di carico. Abbiamo un coefficiente d’attrito che vale:

Nella zona a moto turbolento ( più comune perché sono più comuni i tubi scabri in quanto facilitano lo scambio di calore) la scabrezza incide sulle perdite di carico: più il tubo è scabro più sono le perdite a parità di numero di Reynolds. In questa zona l’andamento del grafico è logaritmico; è quindi interessante notare che se mi trovo in una zona molto turbolenta la curva tende a diventare una retta ed è quindi possibile trovare direttamente il valore l da e / D per ogni valore di Re abbastanza grande.

Nella zona di transizione, come ho già detto prima, il moto è ambiguo e si cerca quindi di dare una descrizione sommaria dell’andamento prendendo valori intermedi ai due casi.

Grazie al diagramma di Moody, noti il numero di Reynolds e il valore di scabrezza relativa del condotto, è possibile conoscere il valore del fattore d’attrito. Basta immaginare un riga verticale in prossimità nel numero di Reynolds e farla arrivare alla curva rappresentante la scabrosità relativa del condotto, da qui si traccia una riga orizzontale fino ad arrivare al valore del fattore d’attrito cercato. Questo è però possibile solo se si conosce Re; in caso contrario bisogna procedere per tentativi (vedremo in seguito un esempio per capirci meglio).

Fino ad ora abbiamo preso in esame tubi cilindrici a sezione circolare, abbiamo quindi sempre parlato di diametri. Tutto quello trattato precedentemente si può però ricondurre a qualunque forma del condotto introducendo il concetto di diametro equivalente. In generale abbiamo:

dove A = Area di sezione, 2P = Perimetro del condotto bagnato dal fluido. Vediamo ora qualche esempio:

In un quadrato di lato l:

In un triangolo equilatero di lato l:

Perdite di carico concentrate

Le perdite di carico concentrate sono anche dette localizzate: questo perché esse sono localizzate in punti precisi del condotto al contrario di quelle distribuite che si trovavano lungo tutto il tubo. Esse si verificano per esempio in prossimità di curve, di rubinetti, di restringimenti o allargamenti della sezione del tubo, etc. Tali perdite non dipenderanno più dalla lunghezza del condotto, ma saranno in funzione di un coefficiente d’attrito che indicheremo con b e che varierà al variare della geometria della figura.

La relazione diventa quindi :

I valori di b per i casi più comuni sono riporati nella seguente tabella:

Lunghezza equivalente

Per velocizzare i calcoli si è introdotto un nuovo metodo per trovare le perdite di carico concentrate facendo riferimento a quelle distribuite. Il concetto è quello di sostituire alla discontinuità un determinato valore di lunghezza del condotto. Avremo:

Un altro metodo per trovare la lunghezza equivalente è per via grafica. Dopo vari esperimenti si è arrivati alla costruzione di diagrammi che ci permettono di stabilire la lunghezza equivalente conoscendo il diametro del nostro condotto ed il tipo di accidentalità localizzata. Nella pagina seguente ho riportato il grafico che si legge con molta facilità: per prima cosa si identifica sulla colonna di destra il valore del diametro del tubo in esame, su quella di sinistra invece si sceglie il valore in base al tipo di accidentalità localizzate, si uniscono i due punti con una retta, l’intersezione di quest’ultima con la colonna centrale identifica il valore della lunghezza equivalente.

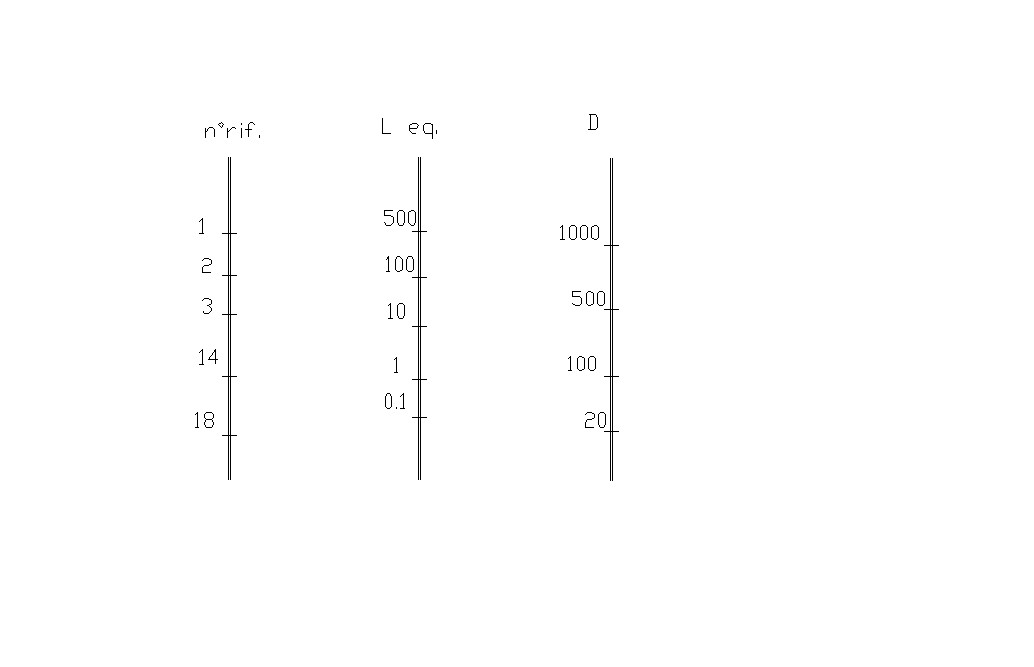
Problemi e risoluzioni

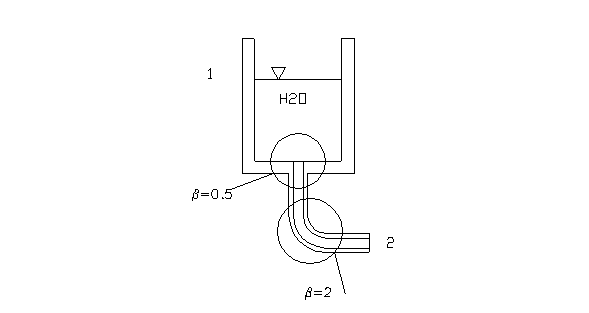Es.1

Il problema ci chiede di determinare la velocità all’uscita e la portata del tubo conoscendo:

H=2m, D=2cm, l=4m, e= 20mm

Per prima cosa applico il teorema di Bernoulli per capire cosa succede all’interno del tubo:

Le pressioni sono entrambe atmosferiche, quindi si elidono a vicenda; avremo che

Notiamo che = dove b =2+0.5=2.5.

Risolvendo e semplificando l’equazione otterrò:

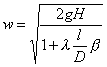
Tale relazione però dipende da l che non è fisso:pertanto per determinare il valore della velocità devo procedere per iterazione.

Conosco e, calcolo e/D e trovo una curva sul diagramma di Moody. Mi costruisco una tabella nella quale registrerò i vari tentativi e grazie alla quale riuscirò ad ottenere la velocità cercata.

N tentativi		Re	l
1			0,023	2,20 m/s
2	2,2	44000	0,0247	2,156 m/s
3	2,156	43000	0,025	2,15 m/s

Sono così arrivata a calcolare la velocità all’uscita del tubo; ora devo trovare la portata: