IIA LEZIONE DEL 15 NOVEMBRE 2001 (ore 16 - 18):
"L’ENTROPIA"
Il disordine
Per determinare se una reazione possa avvenire spontaneamente, sia pure in un tempo illimitato, occorre imparare a misurare l’ordine e il disordine prodotto quando le molecole interagiscono, cioè l’entropia.
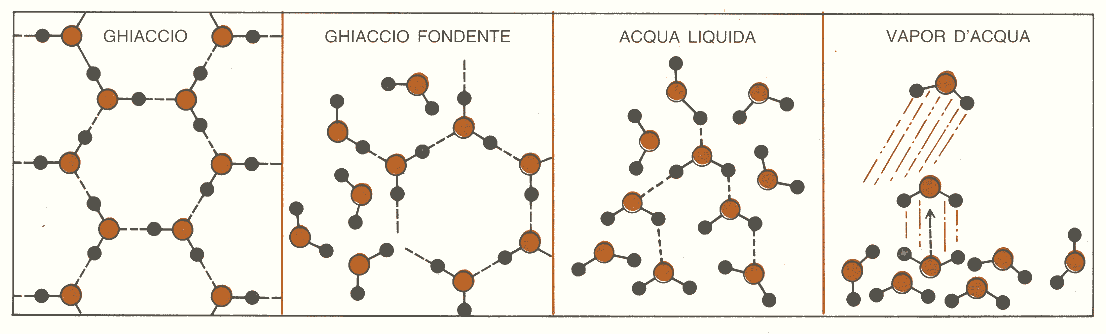
Il fatto che una reazione avvenga o no spontaneamente dipende da due grandezze che talvolta cooperano, ma più spesso sono in conflitto tra di loro: il calore o energia e il disordine o entropia. Nel processo di fusione di un ghiacciolo, l’acqua, mediante il congelamento, può perdere calore, passare ad uno stato di minor energia e provocare un incremento dell’ordine nel cristallo di ghiaccio. Al contrario, un ghiacciolo può passare, attraverso il processo di fusione, ad uno stato di maggior disordine, ma solo se gli viene fornito abbastanza calore da rompere i legami idrogeno presenti nei suoi cristalli (fig. 1). I fattori energetici sono dunque a favore del congelamento, mentre quelli entropici sono favorevoli alla fusione. Possiamo perciò affermare che l’energia gioca un ruolo più importante alle basse temperature, mentre l’entropia è il fattore predominante alle temperature più elevate. La temperatura alla quale queste opposte tendenze si bilanciano rappresenta il punto di fusione del ghiaccio.

Figura 1: il disordine aumenta passando dal ghiaccio al vapor d’acqua.
Il buon senso dice che i processi spontanei sono quelli che portano alla diminuzione di qualche tipo di energia; ma questo spesso non è vero. La maggior parte delle reazioni chimiche spontanee sono esotermiche, cioè sottraggono energia e la liberano sotto forma di calore. Se solamente questi processi fossero spontanei, allora tutti i gas del nostro universo condenserebbero a liquidi, tutti i liquidi in solidi cristallini e il mondo non sarebbe costituito d’altro che di rocce e ghiaccio. Dobbiamo quindi considerare un secondo fattore nei processi naturali, cioè il disordine; le reazioni spontanee non solo tendono ad andare nella direzione in cui si ha una minor energia, ma anche in quella caratterizzata da un maggior disordine. In alcuni casi le due tendenze si rinforzano a vicenda, in altri il risultato è il compromesso delle due opposte inclinazioni.
La grandezza termodinamica entropia presenta quindi alcune interessanti proprietà: in qualsiasi reazione spontanea o processo reale che avvenga in un sistema isolato (cioè in un sistema in cui energia, calore e materia non possono entrare né uscire) si assiste sempre ad un aumento dell’entropia. Ciò significa che, a parte le considerazioni energetiche, le reazioni spontanee sono quelle che vanno nella direzione di maggior entropia.
Come possiamo misurare il disordine? I mezzi per far ciò provengono dalla fisica studiata intorno alla metà dell’Ottocento da William Thomson (più tardi nominato lord Kelvin) e Rudolf Clausius. Essi furono colpiti dal fatto che l’interconversione di calore e lavoro fosse una strada a senso unico: è facile convertire completamente l’energia in calore, mentre la trasformazione inversa non è mai completa. La versione di Thomson della seconda legge della termodinamica stabilisce che è impossibile, per un qualsiasi processo ciclico e ripetibile, assumere calore e convertirlo completamente in lavoro senza perderne una certa aliquota a favore di un sistema a temperature più basse. La seconda legge fa dunque del calore la forma di energia più degradata, facile da ottenere ma non da convertire.
A livello molecolare, l’energia cinetica è un movimento coordinato di tutte le molecole di un solido nella stessa direzione (fig. 2).
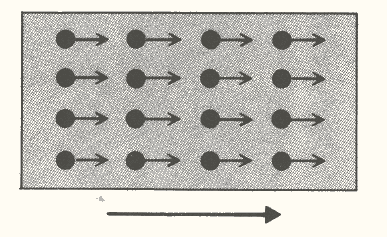
Figura 2.
Il calore di un corpo è il moto scoordinato delle singole molecole attorno alle loro posizioni di equilibrio (fig. 3). L’energia cinetica è un moto organizzato e coerente, mentre il calore è un moto casuale ed incoerente. E’ facile trasformare il primo in secondo, ma è impossibile effettuare il processo in senso opposto.
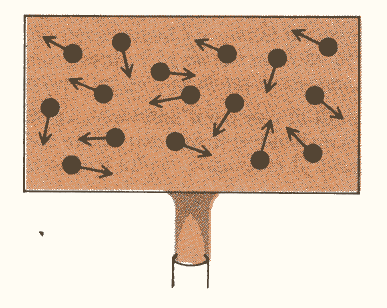
Figura 3.
Una delle conseguenze della seconda legge della termodinamica e degli studi di Kelvin e Clausius fu dunque l’invenzione di una nuova ed utilissima grandezza: l’entropia. Secondo la definizione originaria, questa grandezza dipendeva solo da calore e temperatura: con misure calorimetriche, si può determinare l’entropia di qualunque sostanza ad una determinata temperatura. Tali valori vengono denominati "entropie della terza legge" e si possono trovare in tabulati simili allo schema seguente.
|
SOSTANZA |
ΔH° 298(Kcal/mole) |
ΔG° 298(Kcal/mole) |
S°298 (cal/grado·mole) |
|
Na (g) |
25,98 |
18,67 |
36,72 |
|
Na (s) |
0,00 |
0,00 |
12,20 |
|
C (s, diamante) |
0,45 |
0,69 |
0,58 |
|
C (s, grafite) |
0,00 |
0,00 |
1,36 |
|
CH3OH (g) |
-48,10 |
-38,70 |
56,80 |
|
CH3OH (l) |
-57,04 |
-39,75 |
30,30 |
|
CH3OH (aq) |
-58,77 |
-41,88 |
31,63 |
|
NH4Cl (s) |
-75,38 |
-48,73 |
22,60 |
|
H2O (g) |
-57,80 |
-54,64 |
45,11 |
|
H2O (l) |
-68,32 |
-56,69 |
16,72 |
|
HCl (g) |
-22,06 |
-22,77 |
44,62 |
|
HCl (aq) |
-40,02 |
-31,35 |
13,20 |
Tabella 1: fornisce i valori standard (ΔH°) e le energie libere standard (ΔG°) per la formazione
dei composti a partire dagli elementi, nei loro stati standard; vengono inoltre riportate le entropie (S°) termodinamiche di tutti i composti, calcolate secondo la terza legge della termodinamica.Lo stato fisico del composto è specificato da: (g) = gas, (l) = liquido, (s) = solido, (aq) = soluzione acquosa.
Nonostante i dati sperimentali, è per merito di Boltzmann che riusciamo ad interpretare al meglio i valori delle entropie relative usando il concetto di disordine. Egli, come verrà illustrato meglio più avanti, affermò che:
S = K · log W,
dove K è la costante di Boltzmann e W la probabilità di uno stato del sistema, definita come il numero delle possibili configurazioni che danno origine allo stesso stato termodinamico.
I risultati sperimentali ci forniscono alcune significative conclusioni:
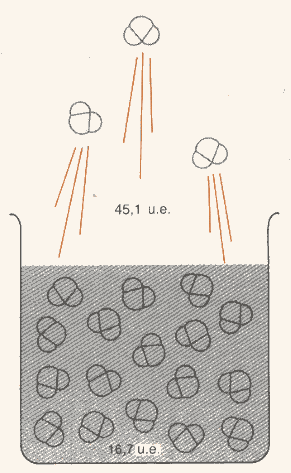
Figura 4: l’acqua evapora a 298 K, con un aumento del disordine di 28,4 unità entropiche per mole.

Figura 5: quando dei cristalli di NH4Cl vengono disciolti in acqua, il disordine aumenta di 17,6 unità entropiche per mole.

Figura 6: quando viene disciolto metanolo allo stato di vapore in acqua, esso diventa più ordinato di 25,2 unità entropiche per mole
Questo è un concetto importante, ma difficile spiegare senza l’aiuto della meccanica quantistica. La sua teoria, semplificata, dice che man a mano che aumentano la massa e le dimensioni di un atomo o di una molecola, l’intervallo tra i livelli energetici diminuisce; un corpo grosso e di massa notevole, con una certa energia totale, ha un numero maggiore di stati quantici possibili, perciò W sarà più grande e S = K·log W risulterà maggiore.
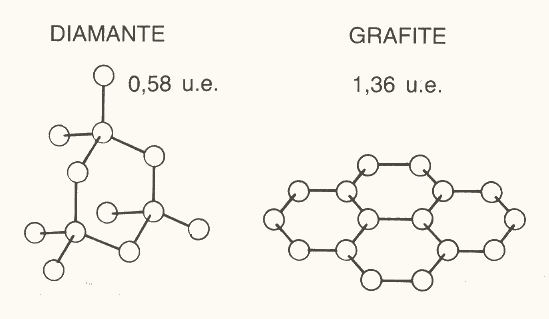
Figura 7: l’entropia è minore in un solido a struttura covalente che in uno con struttura a strati.
I dati derivanti dalla terza legge, sebbene provengano solo da misure termiche, sono in grado di darci alcune informazioni sulla struttura molecolare: queste tendenze delle entropie sono riassunte nella fig. 8, che parte da solidi tridimensionali ed arriva ai gas molecolari. I valori degli elementi puri si trovano invece nella tavola periodica degli elementi.
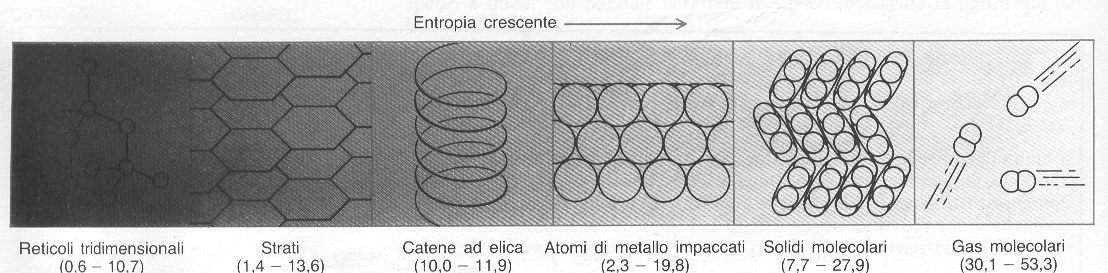
Figura 8: rapporto tra entropia e struttura.
Durante una trasformazione, la variazione di entropia del sistema è pari a:
Δ
S = S2 – S1 = Q / T,dove Q è il calore fornito e T la temperatura assoluta del sistema. L’unita di misura del disordine è pertanto: J / K.
Tale formula si ottiene con un ragionamento per assurdo, cioè considerando degli infinitesimi di secondo nel grafico temperatura - tempo (fig. 9).
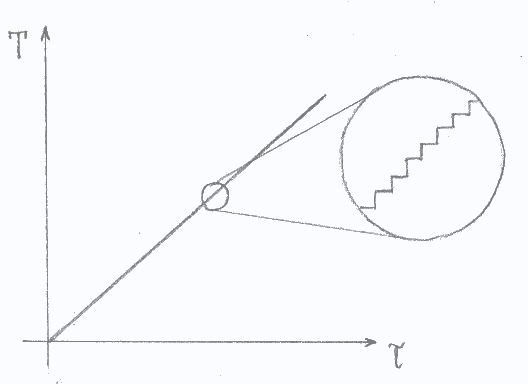
Figura 9.
Possiamo inoltre ricavare la variazione di entropia specifica dividendo per la massa:
Δ
s = ΔS / M.Il lavoro perduto in una reazione si ottiene tramite:
Lp = T0 · ΔS u,
nella quale T0 è la temperatura del termostato più freddo e ΔS u rappresenta la variazione di entropia complessiva dell’universo o di un sistema adiabatico.
Le figure 10 e 11 illustrano ciò che avviene durante trasformazioni isoterme ed adiabatiche: in entrambi i grafici pressione - volume, l’area sottesa dalla curva rappresenta il lavoro; dai diagrammi temperatura – entropia si ricava invece il calore.
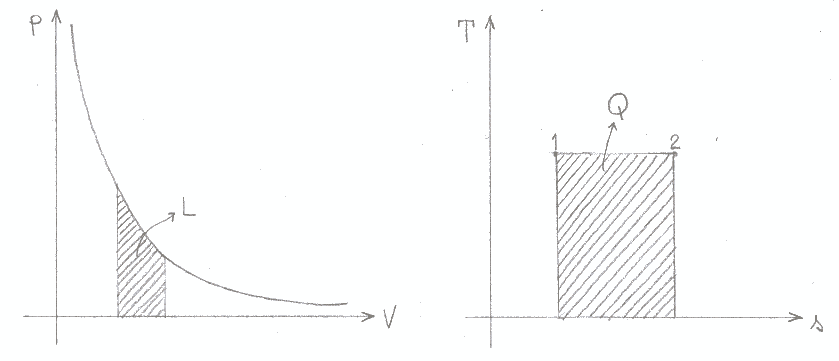
Figura 10: trasformazione isoterma (T = costante).
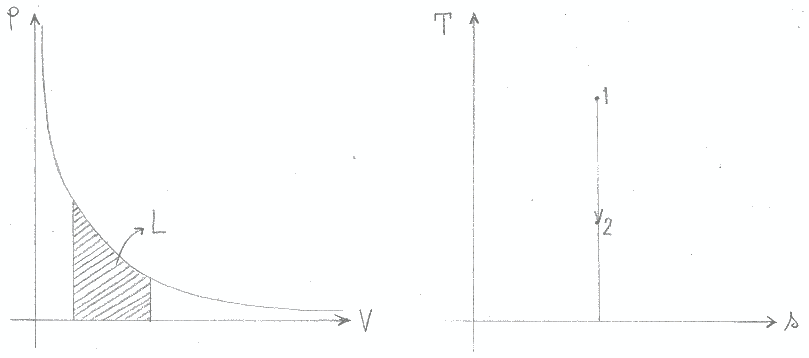
Figura 11: trasformazione adiabatica (Q = costante).
Come si può riscontrare direttamente dalla formula:
Δ
s = q / t,durante una reazione con calore specifico "q" costante, anche l’entropia specifica "s" rimane invariata.
La probabilità
L'affermazione secondo la quale i fenomeni spontanei avvengono sempre in una direzione e mai in quella opposta, è dettata da considerazioni di carattere pratico, che derivano dalle osservazioni stesse dei fenomeni, più che dal tentativo di far valere opportune leggi fisiche.
Se scaldiamo una pentola contenente acqua, tutte le molecole iniziano a muoversi sempre più velocemente ma in maniera disordinata. Qual è la probabilità che, per puro caso, le particelle comincino a muoversi tutte nella stessa direzione, trascinando con sé la pentola ed il muro della cucina? Essa è praticamente pari a zero, ma non c’è nessuna legge fisica o chimica che lo vieti: di fatto sono eventi anch'essi possibili. Sono, però, altamente improbabili, ovvero la possibilità che si verifichino è molto piccola.
Si può dire, perciò, che il senso dell'evoluzione dei fenomeni naturali è regolato dalla probabilità: un sistema compie spontaneamente solo e sempre le trasformazioni caratterizzate dalla massima probabilità.
Per chiarire questo concetto consideriamo ad esempio una molecola di gas, racchiusa in un recipiente diviso in due parti A e B da un setto poroso, attraverso il quale la molecola possa passare. Ricordando che la probabilità che si verifichi un evento è data dal rapporto fra il numero di casi favorevoli e il numero di casi possibili, ovvero:
p = numero casi favorevoli / numero casi possibili,
calcoliamo quale sia la probabilità di trovare la molecola di gas nella parte A del recipiente. Come si vede dalla figura 12 c'è un solo caso favorevole su due possibili, dunque si ha:
p = 1/2
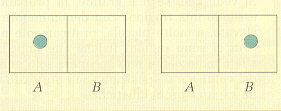
Figura 12.
Se le molecole di gas fossero 2, quale probabilità avremmo di trovarle entrambe in A? I casi possibili sono 4, ma solo uno è favorevole (fig. 13), dunque:
p = 1/4 = 1/22
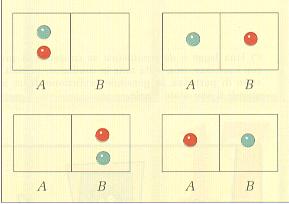
Figura 13.
E se le molecole fossero 3? Avremmo 1 caso favorevole su 8 casi possibili (fig. 14), dunque:
p = 1/8 = 1/23

Figura 14.
Generalizzando il risultato ottenuto a n molecole di gas, la probabilità di trovarle tutte nella parte A è:
p = 1/2n
Si vede che se n è grande, la probabilità p, essendo una frazione con denominatore molto elevato, è molto piccola, praticamente nulla. Non ci sono ragioni fisiche che impediscano alle n molecole di non occupare solo una parte del volume a disposizione, ma piuttosto esistono ragioni probabilistiche.
Dunque, si può affermare che un sistema evolve spontaneamente verso le configurazioni più probabili, e poiché, come abbiamo visto, l'evoluzione spontanea avviene verso stati in cui l'entropia e il disordine aumentano, ne consegue un nuovo significato dell'entropia, legato alla probabilità: le trasformazioni reali sono caratterizzate da aumento del disordine, aumento dell'entropia, aumento della probabilità.
Come anticipato, l’uomo che ha dato un significato molecolare dell’entropia fu Ludwig Boltzmann, un matematico e fisico che operò nella seconda metà del XIX secolo. Egli suggerì per primo che l’entropia fosse una misura del disordine, e diede un significato concreto a quest’ipotesi proponendo che tale grandezza fosse in relazione con il numero dei diversi modi microscopici attraverso cui si può ottenere una situazione ben determinabile ed osservabile sul piano microscopico. Nella legge:
S = K · log W,
il numero di questi modi di ottenere una situazione è rappresentato da W. La costante di proporzionalità K è la costante dei gas per molecola, cioè:
K = R / N,
in cui R è la costante dei gas e N il numero di Avogadro. K venne scelta da Boltzmann in modo tale che la sua entropia statistica potesse essere espressa dalle stesse unità, e misurata sulla stessa scala dell’entropia termodinamica.
La quantità importante nell’equazione, dal punto di vista fisico, è il numero di modi possibili per ottenere uno stato, W. C’è un solo modo per mettere insieme un cristallo perfetto: uno di essi, allo zero assoluto, ha W = 1 e S = K · log1 = 0. Al contrario, il numero di modi per formare una mole di gas è maggiore che nel caso del cristallo; W è maggiore di 1, e perciò l’entropia risulterà positiva. Qualsiasi situazione definita in maniera tale da poter esser descritta in un solo modo o in pochi modi diversi, viene da noi riconosciuta come ordinata; quando uno stato è definibile attraverso tantissimi modi tutti equivalenti, viene detto disordinato.
Come già anticipato, la legge di Boltzmann ci dice che l’oggetto più perfetto ed ordinato che possiamo immaginare in tutto l’universo è un cristallo perfetto allo zero assoluto. Qualsiasi altra condizione è sicuramente più disordinata ed ha entropia positiva.
Entropia ed universo
Se combiniamo le scoperte di Boltzmann con la termodinamica, arriviamo ad uno dei concetti più importanti di tutta la scienza: in qualsiasi processo reale e spontaneo, comprese le reazioni chimiche, il disordine dell’universo aumenta sempre. Infatti la struttura dell’universo, secondo la quale luoghi diversi hanno proprietà differenti, è una forma di ordine, ma ogniqualvolta avviene un processo reale, un po’ di questo ordine viene perso. L’universo porta quindi dentro di sé i semi della sua morte; dal punto di vista dell'energia libera, esso tende continuamente ad esaurirsi.
Quando l’ultima stella morirà, quando l’ultima fonte di calore si spegnerà, l’ultimo composto ricco di energia si sarà consumato e l’universo diventerà una dispersione omogenea di polvere fredda, allora tutto quanto sarà compiuto. Se le leggi della termodinamica sono universalmente valide, non c’è modo di sfuggire a questa "morte per entropia" dell’universo; occorrerà molto tempo, ma sarà inevitabile.
Entropia e tempo
La seconda legge della termodinamica stabilisce che, in qualsiasi regione isolata dello spazio, l’entropia aumenta sempre spontaneamente nel tempo. Il fisico Arthur Eddington ha aggirato questa affermazione dicendo: "a livello macroscopico, tutte le leggi fisiche sono completamente reversibili nel tempo, e le direzioni positiva e negativa del tempo non possono venire definite. A livello macroscopico, il tempo positivo è la sequenza di avvenimenti in cui il disordine di un sistema isolato aumenta". In base all’affermazione di Eddington, la seconda legge non è più una definizione dell’entropia, ma del tempo positivo; il fisico definì perciò l’entropia come "la freccia del tempo".
Esistono almeno tre diverse "frecce del tempo": quella termodinamica, appena discussa; quella psicologica, cioè la direzione in cui noi sentiamo che trascorre il tempo; quella cosmologica, cioè la direzione del tempo in cui l’universo si sta espandendo anziché contraendo.
Indipendentemente dal modo in cui le nostre inclinazioni filosofiche ci portano a considerare l’entropia, occorre ammettere una relazione importante: nell’universo reale il tempo positivo e l’aumento di disordine vanno sempre di pari passo.