IL MOTO
ESTERNO
Il moto esterno, è quella parte della fluidodinamica che studia il moto dei fluidi intorno ai corpi, infatti coinvolge tutti i casi in cui un fluido viene a contatto con la superficie esterna di un corpo. Questo contatto avviene in due modi:
· l’ oggetto è fermo e il fluido si muove intorno ad esso
· il fluido è fermo e l’ oggetto si muove intorno ad esso.
La cosa importante è quindi, il moto relativo tra il fluido e il corpo con cui viene a contatto.
Prendiamo ora come esempio un corpo cilindrico qualsiasi (un palo della luce, una ciminiera,…)
investito dal vento:
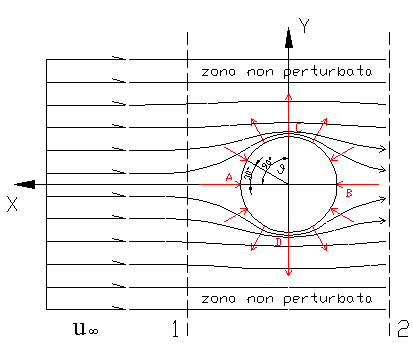
Figura 1
Nel sistema descritto in figura 1, abbiamo un
riferimento cartesiano in cui ![]() è la velocità con cui scorre il fluido
con un profilo di velocità piatto. Vediamo che l’ aria lambisce il solido ma
non lo può attraversare, perciò si sposta lungo la sua superficie. Di
conseguenza, si avverte una diminuzione di velocità e un conseguente aumento di
pressione nel fluido. In particolare nei punti A e B, la velocità è nulla e si
ha una sovrapressione ( detti punti si chiamano: punti di ristagno ) invece, nei punti C e D, in cui il fluido ha
velocità massima, la pressione è minima.
è la velocità con cui scorre il fluido
con un profilo di velocità piatto. Vediamo che l’ aria lambisce il solido ma
non lo può attraversare, perciò si sposta lungo la sua superficie. Di
conseguenza, si avverte una diminuzione di velocità e un conseguente aumento di
pressione nel fluido. In particolare nei punti A e B, la velocità è nulla e si
ha una sovrapressione ( detti punti si chiamano: punti di ristagno ) invece, nei punti C e D, in cui il fluido ha
velocità massima, la pressione è minima.
Un corpo può essere
investito da due tipi di azioni:
· Azioni orizzontali ( per esempio dovute dal vento )
· Azioni verticali
Quando incontra un ostacolo, il fluido lo dovrà
evitare e perciò si creano sforzi:
·
pressioni o
depressioni perpendicolari al corpo
·
sforzi tangenziali
causati dalla viscosità del fluido
Lo sforzo tangente (τ) è proporzionale alla viscosità del fluido, vediamo infatti che l’ olio grezzo produce sforzi tangenti molto forti, mentre quelli della benzina sono quasi trascurabili. Osserviamo inoltre, che gli sforzi normali producono F (la forza di trascinamento) che aumenta più il fluido è viscoso perché vengono implicate anche le componenti tangenti della forza sul corpo. A questo proposito possiamo vedere nella seguente tabella la viscosità di alcuni fluidi:
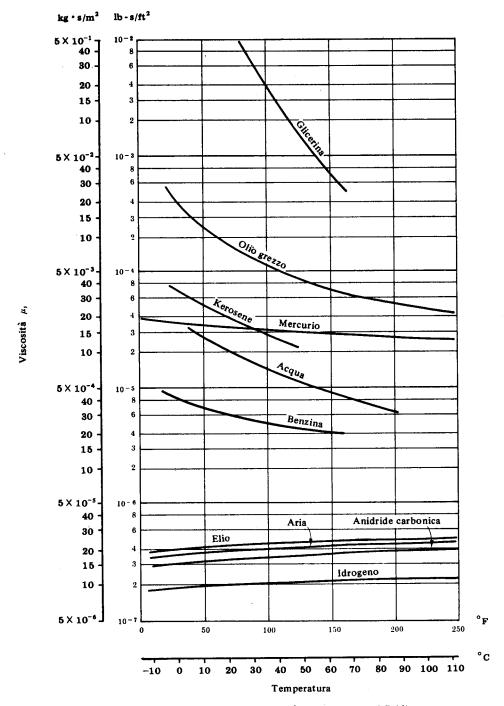
Tabella 1
Anche un fluido ideale provoca sforzi di
trascinamento; per esempio, tornando alla figura 1, vediamo che se il fluido è ideale la pressione che esso
esercita sulla superficie posteriore del cilindro è identica a quella
esercitata nella faccia anteriore (quindi: ![]() ). In questa ipotesi la velocità gode di una simmetria
sferica, quindi anche la pressione può beneficiare di questa simmetria. Il
risultato è che gli sforzi normali si equilibrano perfettamente e il corpo
rimane fermo e fluido. Un corpo che gode di queste simmetrie immerso in un
fluido ideale (v = o), non viene né
trascinato perché la risultante degli sforzi normali è nulla, né messo in
rotazione dal fluido stesso perché gli sforzi tangenziali sono nulli.
). In questa ipotesi la velocità gode di una simmetria
sferica, quindi anche la pressione può beneficiare di questa simmetria. Il
risultato è che gli sforzi normali si equilibrano perfettamente e il corpo
rimane fermo e fluido. Un corpo che gode di queste simmetrie immerso in un
fluido ideale (v = o), non viene né
trascinato perché la risultante degli sforzi normali è nulla, né messo in
rotazione dal fluido stesso perché gli sforzi tangenziali sono nulli.
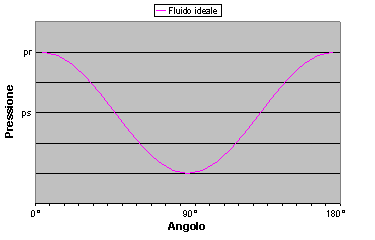
Grafico 1
Consideriamo adesso i fluidi reali, ovvero
i fluidi che possiedono una certa viscosità μ, facendo sempre riferimanto alla situazione descritta in fig.1.
Dato che l’ aria possiede una certa viscosità, si
sviluppa un certo attrito con la superficie del cilindro. In questo caso, parte
dell’ energia cinetica viene presa per scambio termico e come conseguenza, l’
aria che attraversa la sezione 1 ha maggiore energia rispetto a quella che
passa attraverso la sezione 2. Avremo perciò, che la componente di forza
normale alla superficie non avrà più posizione simmetrica, ma il suo valore
tenderà a diminuire muovendosi da 0° a
180° in senso antiorario. La pressione avrà quindi, il seguente andamento:
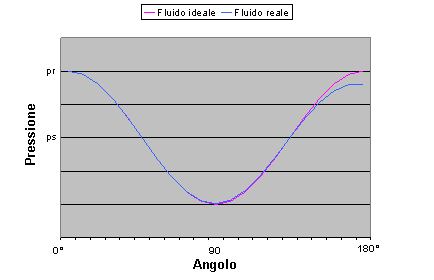
Grafico 2
RESISTENZA
E PORTANZA
Ogni volta
che un oggetto viene posto in un fluido in moto, o si muove attraverso un
fluido in quiete, nasce una forza agente nella direzione del moto del flluido
rispetto all’ oggetto stesso (resistenza D),
e può nascere una normale alla stessa direzione (portanza L). Dette forze si possono esprimere così:
![]()
![]()
![]()
A
(l’ area frontale) è una superficie
caratteristica, di solito la superficie o proiezione medesima, normale alla
direzione del moto. L area frontale è il fattore di proporzione tra
pressione e forza di trascinamento ed è proporzionale al coefficiente di
aerodinamica (Cr) e alla viscosità del fluido.
![]()
Le equazioni sopracitate (D e L), definiscono il
coefficiente di resistenza ![]() e quello di
portanza
e quello di
portanza ![]() ; tranne pochi casi
essi debbono essere sempre cercati sperimentalmente. Generalmente dipendono dal
numero di Raynolds, che si può calcolare in funzione al Cr, per figure semplici come la sfera e il cilindro, nella seguente tabella.
; tranne pochi casi
essi debbono essere sempre cercati sperimentalmente. Generalmente dipendono dal
numero di Raynolds, che si può calcolare in funzione al Cr, per figure semplici come la sfera e il cilindro, nella seguente tabella.
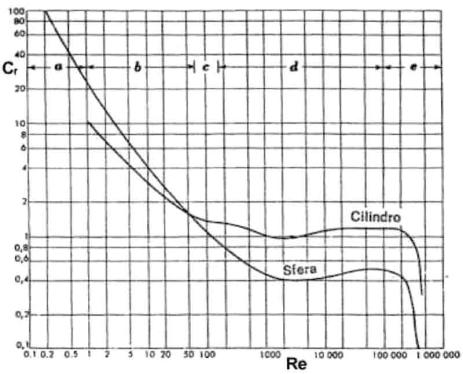
Grafico 3
Il numero di Raynolds è dato, per la sfera e il
cilindro, da ![]() per la lunghezza caratteristica che è data
dal diametro.
per la lunghezza caratteristica che è data
dal diametro.
![]()
Le forze
di resistenza e di portanza sono causate dalla somma delle forze tangenziali e
normali che operano sulla superficie del corpo. La resistenza dovuta alle
azioni tangenziali si chiama attrito
superficiale, o resistenza viscosa; è il tipo di resistenza più importante, in
cui l’ area di superficie parallela alla direzione del moto è grande rispetto
all’ area proiettata, normale alla direzione del moto. Per esempio, la
resistenza d’ attrito superficiale è responsabile di tutta la resistenza nel
caso della lastra piana parallela al letto del vento. La resistenza dovuta a sforzi normali si chiama resistenza di
forma, o di pressione, più importante e spesso predominante per i profili
tondeggianti. Il fluido non è senza attrito e lo strato limite esiste e cresce
più rapidamente con con un gradiente di pressione avverso, e se quest’ ultimo è
abbastanza grande si può verificare la separazione. Il grande strato limite o
onda, sulla parte posteriore del corpo,
risulta in una pressione minore di quella che si otterrebbe nel moto senza
attrito. Questa pressione ridotta risulta in una forza in direzione del moto.
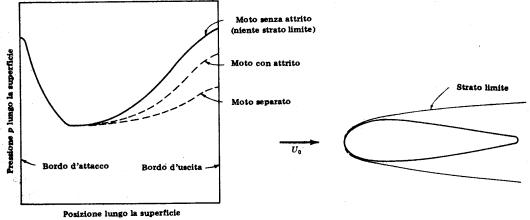
Figura2
Vediamo qui che per ridurre il gradiente di
pressione avverso sulla parte posteriore del corpo, e, se possibile, prevenire
la separazione. Ciò significa che sulla parte posteriore sopradescritta,
dovremmo avere una curvatura progressiva; però se il corpo è troppo lungo,
perdiamo il guadagno ottenuto riducendo la resistenza di pressione, per l’
aumento della forza d’ attrito superficiale. Progettare un corpo in vista della
minima resistenza significa dunque, cercare un compromesso tra resistenza d’
attrito superficiale e resistenza di pressione.
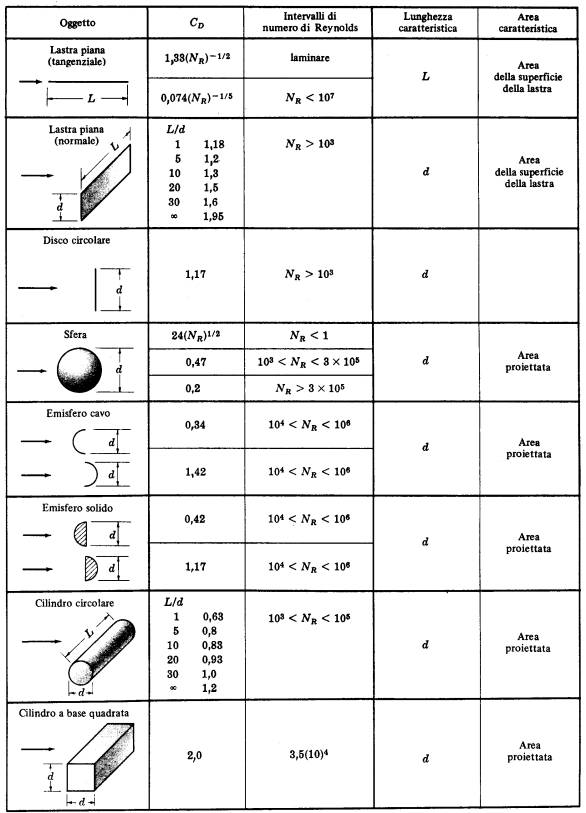
Tabella 2
(coefficienti
d’ attrito)
I PROFILI ALARI
Ci occuperemo ora della forma del profilo
(essendoci dedicati per il momento a forme semplici) e della causa fisica della
circolazione. Abbiamo visto che un cilindro dotato di rotazione genera
circolazione, ma cosa potremmo ricavare da un profilo alare che non può
circolare?
Abbiamo visto che la portanza è dovuta
alla circolazione: e indubbiamente avremo circolazione intorno ad un profilo. Riferendoci
alla figura 4, notiamo che il punto singolare sul bordo d’ attacco, là dove la velocità secondo la
teoria del moto potenziale deve essere infinita, non può esistere una corrente
reale, e tale corrente si regolerà
automaticamente, in modo da spostare il punto di ristagno verso il bordo
d’ uscita e di eliminare, in questo modo, il punto singolare. Il valore della
circolazione Г attorno al profilo, è giusto
quel tanto che serve per spostare il punto di ristagno verso il bordo d’ uscita.
Per effettuare questo spostamento, Г deve essere negativa, e quindi la portanza ![]() deve essere positiva, come si vede in figura.
deve essere positiva, come si vede in figura.
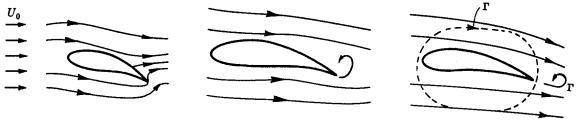
Figura 3
All’ avviarsi della corrente, il moto potenziale
si presenta come in figura 3; il punto di ristagno si sposta verso la
parte posteriore e si forma un piccolo vortice, che si stacca e va a perdersi a
valle. Per il teorema di Kelvin, la circolazione totale nel fluido deve essere
costante nel tempo, e quindi attorno al profilo si genera una Г uguale al vortice portante,
ma di segno opposto. La circolazione totale nel fluido deve rimanere pari a
zero, ma il suo valore attorno al profilo è un numero negativo. Il vortice
resta indietro, e si perde nel campo di velocità.
Diagramma per l’ ala di un aereo
(Il Cx dovrebbe essere 7 – 8 volte il Cy)
Conta il
profilo dell’ aereo, non la lunghezza dell’ ala.
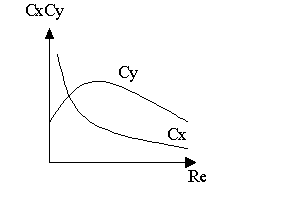
Grafico 4
LA
GALLERIA DEL VENTO
Le gallerie del vento
sono strutture (anche di dimensioni ragguardevoli) utilizzate per compiere
studi fluidodinamici e in particolare aerodinamici; infatti, vi si effettuano
esperimenti per la misura degli sforzi che il vento provoca su una
apparecchiatura (automobile, radiatore, aereo, ecc.). In questo modo si evita
di ricorrere a metodi di calcolo numerici assai complessi, visto anche che in
questo campo, a regimi ad alta quantità di Reynolds (regime turbolento), non si
ha grande rigore matematico.
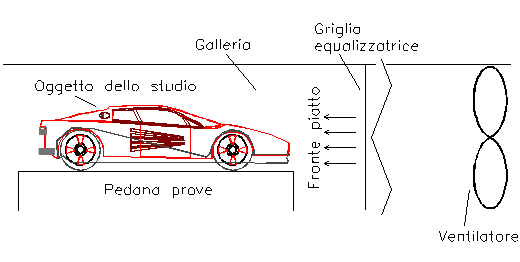
Figura 4
Eccone la descrizione.
Il ventilatore genera un flusso di aria
all’interno della galleria di forma cilindrica con una certa velocità; tale
aria viene fatta passare attraverso una griglia equalizzatrice di flusso che
serve per creare un profilo di velocità piatto; l’aria investe quindi l’oggetto
dello studio e se non sono presenti gas di scarico derivati dall’uso dei
motori, il flusso generato (ancora carico di ![]() ) viene incanalato
nel condotto di raccordo che lo ricicla chiudendo il circuito (l’aria con il
tempo si scalda e va anche raffreddata).
) viene incanalato
nel condotto di raccordo che lo ricicla chiudendo il circuito (l’aria con il
tempo si scalda e va anche raffreddata).
Nel caso specifico delle gallerie
automobilistiche, il veicolo è situato su una pedana che può essere del tipo
rappresentato in figura 6. In questo caso, la pedana è costituita di un nastro
scorrevole (che simula il movimento del terreno) con trasduttori di forza usati
per la misura dei carichi aerodinamici scaricati sul suolo e sensori di
contrasto per misurare la pressione nei vari punti.
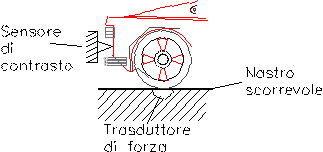
Figura 5
Visto che il profilo inferiore dell’oggetto può
essere differente da quello superiore, la risultante può essere portante (aereo) o deportante ¯ (automobile). Gli aerei hanno un rapporto di
almeno 5:1 tra forza portante e forza d’attrito (l’aliante, che è l’aereo più
efficiente, arriva a 10:1). Per le auto, al contrario, maggiore è la forza
deportante e maggiore è la tenuta.
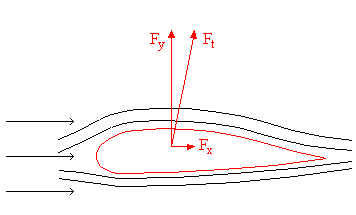
Figura 6
ESEMPIO DEI MODELLI IN SCALA
Per esempio, alla Dallara, ho una vettura vera di
lunghezza pari a 4m (L) che raggiunge
una velocità di 300 km/h e una vettura in scala 1:2 di 2m (L’). Il numero di Reynolds (Re)
deve essere lo stesso in entrambe le auto, quindi Re=Re’.
![]()
quindi: ![]()
Se trascuriamo la lunghezza, bisogna raddoppiare
la velocità.
SPINTE
PRODOTTE DAL VENTO SUGLI EDIFICI
Se progetto una superficie che lavora come l’ ala
di un aereo, il vento la farebbe decollare, ma se non ho superficie, lo sforzo
di trascinamento diventa ininfluente. Invece un ponte con forma ricurva che
possiede una struttura metallica reticolare, non rischia di venire portato via
dal vento perché quest’ ultimo gli passerebbe attraverso.
ESERCIZI
Esercizio 1
A che velocità cadono le gocce di pioggia?
Supponiamo che le gocce siano sfere e che quando
si impattano sulla superficie, assumano la forma di un dischetto schiacciato:
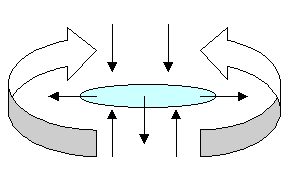
Figura 1
Consideriamo una goccia piccola che scende piano. Quest’
ultima, di diametro 1mm e densità ![]() , cade senza subire
deformazioni. Conoscendo la densità dell’ aria,
, cade senza subire
deformazioni. Conoscendo la densità dell’ aria, ![]() , calcolare la
velocità con cui cade la goccia.
, calcolare la
velocità con cui cade la goccia.
Sulla goccia agiscono alcune forze:
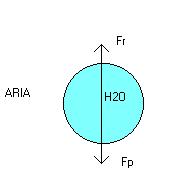
Figura 2
·
La forza peso Fp rivolta verso il basso:
![]()
(1)
·
La forza resistente
di attrito, diretta verso l’ alto:
![]()
(2)
Dato che la velocità di
caduta è uniforme quando la due forze (Fp e Fr) sono uguali
calcoliamo, sostituendo in (2), Fr:
![]()
Adesso calcoliamo V che
è il volume della goccia e ![]() che è la sua area
frontale, in funzione del diametro D:
che è la sua area
frontale, in funzione del diametro D:
![]() e
e ![]()
Sostituendo otterremo:
![]()
Dopo aver semplificato
otteniamo la velocità ![]() nel seguente modo:
nel seguente modo:
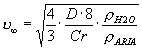
La velocità è quasi
proporzionale al diametro della goccia.
Esercizio
2
Supponiamo ora, di essere in mare e lasciamo
cadere un masso: noteremo che quest’ ultimo viene respinto dall’ acqua per
opera della forza di galleggiamento (Fg).
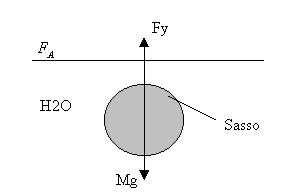
Figura 1
Dati:
![]()
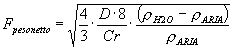
![]()
![]()
![]()
![]()
Quindi calcolo il Numero di Reynolds, per
potere ricavare, in seguito, il ![]() :
:
![]()
Ora che ho calcolato il numero di Reynolds, e dato che anche il ![]() dipende dalla velocità, devo procedere a tentativi
ipotizzando valori di velocità ( in questo caso
dipende dalla velocità, devo procedere a tentativi
ipotizzando valori di velocità ( in questo caso ![]() ).
).
Primo tentativo:
Vado sul
diagramma (grafico3) che mi da il Cr per la sfera. In questo caso il Cr vale circa 1.7 e calcolo:
![]()
In questo caso il Re non va bene e di conseguenza, devo
ricalcolare il numero di Reynolds.
Secondo tentativo:
![]()
Prendo anche questa volta il Re e vado sul diagramma a cercare il Cr corrispondente. In questo secondo caso il Cr vale circa 1.2 e calcolo:
![]()
Anche da questo calcolo, vediamo che il Cr non va ancora bene e procedo
calcolando per la terza volta il numero di Reynolds, sempre andando a
sostituire la velocità (u) precedente.
Terzo tentativo:
![]()
Vado anche questa volta sul diagramma che mi da il
Cr, che in questo caso vale 0.8, e
trovo:
![]()
Devo procedere fino a quando non trovo un valore
di velocità che si discosta da quello calcolato in precedenza, di una quantità
minore della tolleranza richiesta.
Esercizio 3
In una linea elettrica, I diametri dei pali e dei
fili sono rispettivamente 10cm e 3mm. I pali sono alti 10m e
il filo è lungo 50m. Il vento soffia in direzione ortogonale alla linea
a una velocità di 100km/h.
Determino, dunque, la forza di trascinamento del filo![]() e del palo
e del palo ![]() e il momento flettente.
e il momento flettente.
Dati:
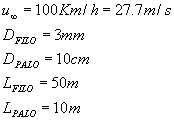
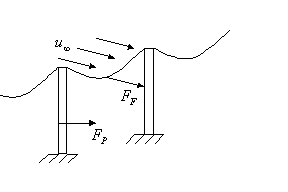
Figura 1
Il palo (P)
tende a ruotare e abbiamo un momento flettente che è una forza per un braccio e
si misura in ![]() . Ora andiamo a
calcolare la forza sul filo (
. Ora andiamo a
calcolare la forza sul filo (![]() ) e il numero di
Reynolds (Re) per il filo:
) e il numero di
Reynolds (Re) per il filo:
![]()
![]()
Una volta trovato il Re, vado sul diagramma (grafico
3) per il cilindro (dato che stiamo avendo a che fare con un filo) e trovo
il ![]() che vale circa 1.
che vale circa 1.
![]()
Anche in questo caso vado sul diagramma (grafico 3) e trovo il ![]() per il palo che vale circa 1,2 e calcolo la forza esrcitata da u sul palo:
per il palo che vale circa 1,2 e calcolo la forza esrcitata da u sul palo:
![]()
In conclusione abbiamo questa situazione:
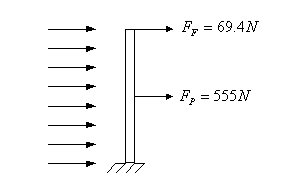
Figura 2
Così possiamo calocolare il momento flettente ![]() come segue:
come segue:
![]()
Esercizio
4
Consideriamo ora, un palazzo di 30m di altezza e
80m di base soggetto alle forze del vento che soffia perpendicolare all’
edificio con una velocità ![]() di 100 Km/h cioè 27.77 m/s.
di 100 Km/h cioè 27.77 m/s.
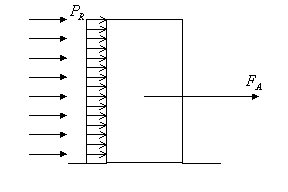
Figura 1
Dati:
H=30m
B=80m
![]()
Si calcoli quindi, la pressione dovuta dal vento e
la forza di trascinamento di quest’ ultimo nei seguenti modi:
![]()
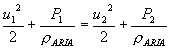
Dove:
P è
la pressione del vento
u è
la velocità del vento
![]() è la densità dell’ aria
è la densità dell’ aria
![]()
![]()
![]()
Osservazioni:
Un caso particolare sono le coperture curve come,
per esempio, alcuni palazzetti dello sport:
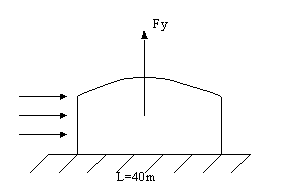
Figura 1
In questa situazione, il Cy può arrivare a valere
10 quindi avremo:
![]()
Il calcestruzzo lavora bene a compressione ma non
a trazione (per esempio, quando tira il vento). Invece un materiale come il
ferro lavora bene a trazione (resiste perciò alle spinte del vento) ma non a
compressione.
Abbiamo detto che il Cy nel caso delle coperture ricurve arriva a livelli
molto alti, ma non per questo l’ azione orizzontale non esiste. Infatti il Cx
c’ è ma è molto basso, infatti può essere ![]() .
.