Trasformazioni in un sistema chiuso

Le variabili di stato

In un sistema chiuso, che non scambia cioè materia con l’esterno, è necessario considerare le tre variabili che lo caratterizzano, definite “VARIABILI DI STATO”: PRESSIONE, VOLUME e TEMPERATURA.

Il loro variare all’interno di un sistema chiuso da luogo ad una TRASFORMAZIONE da uno stato iniziale ad uno finale.

Equazione di stato dei gas perfetti

Esiste un’equazione che mette in relazione le tre variabili di stato tra loro, è detta EQUAZIONE DI STATO dei gas perfetti.

(1)

Dove p, V e T, indicano rispettivamente le tre variabili di stato pressione, volume e temperatura; m la massa del gas espressa in Kg, R la costante universale dei gas, pari a 8,314 J/Kmol (ma deve essere determinata sperimentalmente per ogni gas non perfetto!)

Essendo sia m, che R costanti in un sistema chiuso dalla (1) deriva:

costante (2)

N.B: La funzione di stato conterrebbe al posto di m il simbolo n che sta ad indicare il numero di moli di gas, ma per la nostra utilità è stata espressa mettendo in evidenza la massa del gas!

In natura non esiste, ovviamente, un gas perfetto, è un’astrazione che si avvicina di molto alla realtà se si considera il gas a bassa densità.

Le trasformazioni dei gas

Alla luce di quanto affermato mediante l’equazione di stato è possibile definire le quattro possibili trasformazioni di un gas:

· ISOCORA: (fig. 1) A volume costante; in questo caso la trasformazione vedrà legate proporzionalmente pressione e temperatura, infatti dalla (2) ricaveremo:

se costante costante (3)

· ISOBARA: (fig. 2) A pressione costante; anche in questo caso le variabili Volume e Temperatura, saranno direttamente proporzionali; infatti, sempre dalla (2):

se costante costante (Legge di Charles e Gay-Lussac) (4)

· ISOTERMICA: (fig. 3) A temperatura costante; in questo caso il rapporto tra le variabili Pressione e Volume sarà inversamente proporzionale, infatti dalla (2):

se costante costante (Legge di Boyle) (5)

· ADIABATICA: (fig. 4) In assenza di scambi di calore con l’esterno del sistema, ammettendo cioè l’ipotesi di poter isolare completamente il sistema dall’esterno in modo che esso non assimili ne dissipi calore, ricaviamo facilmente dall’equazione del primo principio della Termodinamica che:

essendo (6)

Bilanciamento energetico

Considerando adesso tutte e quattro le trasformazioni, analizziamo il comportamento del sistema in un passaggio da uno stato all’altro, e calcoliamone il bilanciamento energetico.

Consideriamo dunque tre trasformazioni dallo stato A, definito da una pressione PA un volume VA ed una temperatura TA, allo stato B, definito da PB e VB e TB, associate alle lettere a, b, c, d.

a) Il lavoro La compiuto nella trasformazione a è dato dall’area del rettangolo che ha per lati e e quindi sarà dato dall’equazione:

(7)

Deriva quindi dal primo principio della termodinamica l’equazione:

(8)

Ma in un sistema chiuso, essendo l’energia totale la somma di tutte le energie che interessano il sistema, ed essendo soltanto l’energia interna a variare e a condizionare la variazione dell’energia totale, possiamo riscrivere l’equazione del primo principio della termodinamica nel seguente modo:

(9)

la (8) potrà allora essere riscritta così:

(10)

b) Il lavoro Lb compiuto nel percorso b, invece, sarà dato dall’area del trapezio che avrà per base maggiore PA, per base minore PB e per altezza la differenza VB-VA. Quindi:

(11)

Come prima, ovviamente, possiamo calcolare Qb:

(12)

c) Calcolare il lavoro compiuto dal sistema lungo il cammino c, può sembrare più complicato ma alla fine il valore ottenuto sarà uguale alla variazione di energia, essendo Qc = 0. Si avrà allora:

(13)

Sappiamo inoltre che l’energia contenuta in un gas perfetto è data dall’equazione:

(14)

Quindi:

(15)

Mettendo insieme le equazioni dei due stati del sistema avremo:

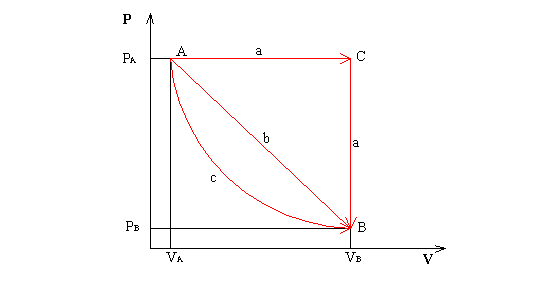
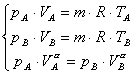con (16)

Ricaviamo così da questo sistema, prima

(17)

e poi (18)

unendo questi risultati con la (15) avremo che il lavoro per il percorso c sarà dunque:

(19)

N.B: In tutti e tre i casi comunque, la differenza sarà uguale; da questo si può dedurre che il primo principio della termodinamica è una funzione di stato, dipendente cioè non dal cammino percorso ma soltanto dai due stati, iniziale e finale, della trasformazione!

ESERCIZIO

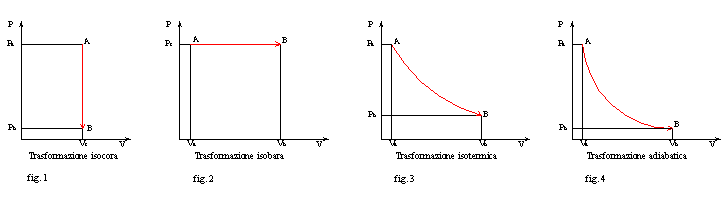
Consideriamo un cilindro contenente aria che passa da uno stato A ad uno stato B, nei tre modi sopra citati.

Supponiamo che siano:

pA = 32 bar = 3.200.000 Pa, VA = 1 m³, TA = 600 K

pB = 1 bar = 100.000 Pa, VB = 8 m³.

Calcoliamo dunque la quantità di calore Q e il lavoro L per tutte e tre le trasformazioni:

c) Ricaviamo, riscrivendo la (17) e la (18) con i dati dell’esercizio, che:

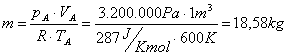(20)

(21)

Possiamo dunque ricavare il lavoro compiuto nel percorso c, essendo :

(22)

Che sarà ovviamente di segno positivo poiché il lavoro sarà compiuto dal sistema!

(23)

b) Per il percorso b il lavoro, come visto sarà dato dall’area del trapezio, cioè:

(24)

A questo punto sarà facile calcolare la quantità di calore:

(25)

c) Per questa trasformazione il lavoro sarà invece dato dall’area del rettangolo che ha per lati VB – VA e PA; cioè:

(26)

e quindi:

(27)