Introduzione *

Superficie (p,v,T) *

Diagramma (p,T) *

Diagramma (p,v) *

La ‘materia’, può venire definita come tutto ciò che ha massa, occupa spazio e possiede energia. Presentandosi sotto diverse forme, essa si distingue, a seconda che siano più o meno intense le forze di coesione che si esercitano tra molecola e molecola, oltre che per le sue proprietà chimico–fisiche, per i suoi stati di aggregazione:

solido (S) liquido (L) aeriforme (V).

Infine, passando da uno stato di aggregazione all’altro, la materia può dare origine a stadi intermedi: S-L, L-V, S-V; oppure trasformarsi in energia, fornendo o prelevando calore al sistema. Importante è ricordare che materia e energia non si possono né creare né distruggere.

In particolare, vengono presi in considerazione sistemi chiusi chimicamente omogenei, ossia sistemi costituiti da sostanze chimicamente pure (es. acqua o alcool, ossigeno o azoto), caratterizzati da massa interna costante (ad esempio può essere una sostanza contenuta in un recipiente chiuso e sigillato). Anche sostanze non chimicamente pure, come l’aria, possono talvolta essere considerati tali, purché le caratteristiche chimiche dei singoli componenti che le formano siano simili.

In questa sede vengono presi in considerazione sistemi specificatamente omogenei, e in particolare viene analizzato il comportamento termodinamico dell’acqua.

Per definire lo stato termodinamico in cui una sostanza si trova, una volta identificato l’elemento che compone il sistema che si vuole analizzare, si considerano le tre grandezze fondamentali:

• Pressione assoluta ® p (Pascal)
• Volume specifico ® v (m³/Kg)
• Temperatura assoluta® T (Kelvin)

Partendo da queste è possibile tramite funzioni di stato determinarne altre, quali entropia (s) ,entalpia (h), energia interna (u).

Le grandezze p, v, T sono tra loro legate tramite un’equazione di stato, che ne limita l’indipendenza.

Per individuare il numero di grandezze minime necessarie per definire un sistema si fa riferimento alla regola delle fasi di Gibbs:

Dove:

P = numero delle grandezze indipendenti

M = numero delle componenti chimiche inserite nel sistema

F = numero delle fasi presenti nel sistema

E’ quindi possibile sintetizzare il legame esistente tra il numero di fasi e il numero di variabili, nel seguente modo:

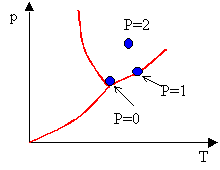
Fig.1- Diagramma (p,T) che rappresenta il numero di fasi

Esempio 1

Considerando un sistema chiuso (immaginiamo ad esempio una pentola sigillata) formato da solo vapore acqueo, avremo M pari a 1, in quanto si considera un sistema omogeneo, e F uguale a 1, perché l’acqua si trova in un solo stato, quello gassoso, e quindi, data l’equazione

il numero delle grandezze indipendenti del nostro sistema sarà 2, segue cioè che la terza variabile viene determinata dalle altre due.

Esempio 2

Se invece prendiamo in considerazione un sistema chiuso omogeneo misto, cioè composto da una sostanza presente in due fasi diverse - ghiaccio che si sta sciogliendo - si ha

e il sistema quindi non ha più due gradi di libertà (o parametri indipendenti) ma 1, dal quale è possibile determinare gli altri due.

Il cambiamento dello stato fisico di una sostanza può perciò essere descritto da un riferimento cartesiano in tre dimensioni, chiamato superficie (p,v,T), avente su ognuno dei tre assi di riferimento una variabile di stato. Ad ogni punto della superficie corrisponde un solo stato fisico di equilibrio del sistema.

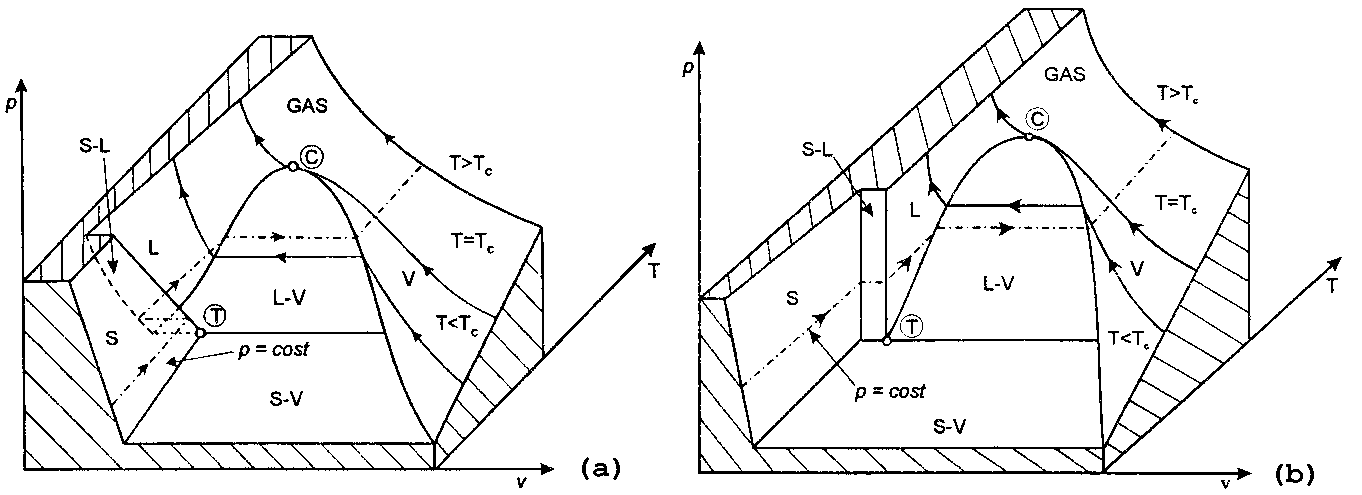
Fig. 2- Superficie (p,v,T) dell’acqua (a) e delle altre sostanze in generale (b).

La fig. 2a rappresenta il comportamento dell’acqua, che cresce di volume nel passare dallo stato liquido a quello solido.

La fig. 2b descrive invece il comportamento della maggior parte delle sostanze (ad es. olio) che aumentano di volume durante il processo di fusione e diminuiscono di volume durante la solidificazione.

Sulla superficie sono rappresentati tutti i possibili stati fisici della sostanza:

• Le zone S, L, G sono caratterizzate da una sola fase;
• Le zone intermedie S-L, L-G, S-G presentano due fasi;

• Punto triplo (punto T). Punto nel quale si ha la compresenza di tre fasi, essendo la sostanza presente allo stato liquido, solido e aeriforme contemporaneamente. La percentuale di distribuzione dipende dall’energia interna: tanto maggiore è, tanto minore sarà la percentuale di ghiaccio.
• Punto critico (punto C). Punto di flesso della curva a temperatura costante definita isoterma critica.

Le curve isoterme, in particolare, evidenziano la possibilità di entrare nella zona di equilibrio liquido-vapore aumentando la pressione: se la temperatura è minore a quella critica, l’isoterma, e quindi la sostanza, passerà per arrivare allo stato liquido da quello L-V; se invece la temperatura è maggiore, cioè l’isoterma si trova al di sopra di quella critica, la sostanza non passerà dalla fase intermedia.

In base a questa distinzione si preferisce parlare di vapore per la zona al di sotto dell’isoterma critica, e di gas per quella al di sopra.

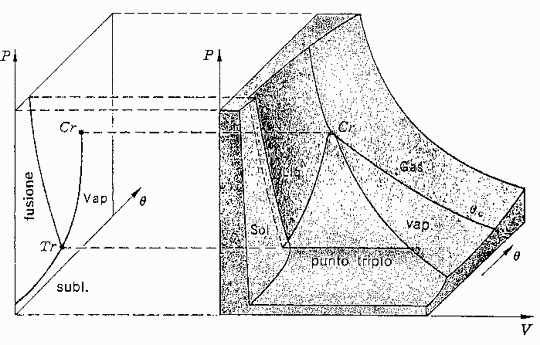
Fig. 3- Passaggio da una superficie (p,v,T) a un grafico bidimensionale

Proiettando la superficie (p,v,T), come nella fig. 3, sui piani cartesiani si ottengono diagrammi bidimensionali che ne facilitano la comprensione.

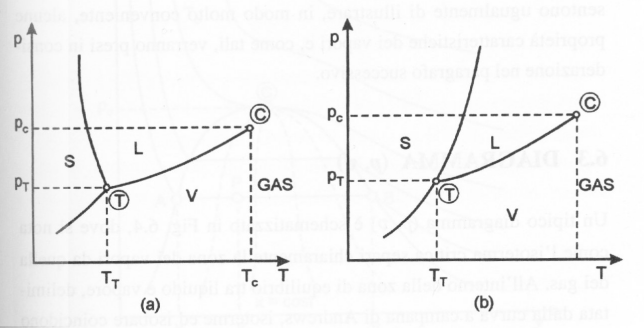
Fig. 4- Grafico (p,T) dell’acqua (a) e della maggioranza delle sostanze (b)

In particolare proiettando il grafico tridimensionale sul piano pressione-temperatura è possibile individuare le diverse fasi (fig. 4).Le tre curve sono chiamate curve d’equilibrio e rappresentano le transizioni di fase (fig. 5) ottenute togliendo o fornendo calore al sistema. Aumentando la temperatura, infatti, si ottiene un aumento dell’energia cinetica (movimento) delle particelle che si allontanano le une dalle altre, allentando sempre più le forze di coesione: il solido passa così allo stato liquido (fusione), per proseguire poi fino a divenire vapore (evaporazione). Al contrario diminuendo temperatura le particelle aumentano il loro stato di aggregazione: il vapore diventa acqua (condensazione) fino a solidificarsi (solidificazione). Per alcune sostanze, inoltre, è possibile che si verifichi il passaggio diretto da solido a gas (sublimazione) e viceversa (condensazione o brinamento).

Fig. 5- Schema che illustra la denominazione dei passaggi di stato

A differenza di quanto accade per la maggior parte delle altre sostanze (fig. 4b) nel caso dell’acqua (fig. 4a) la temperatura del punto di fusione del ghiaccio è inferiore a quella del punto triplo.

Esempio 3

Col fenomeno dell’abbassamento del punto di fusione all’aumentare della pressione è possibile spiegare lo scorrimento dei ghiacci nel loro letto. Gli strati di ghiaccio sottostanti, in conseguenza della pressione prodotta dal peso degli strati sovrastanti, fondono anche a temperature inferiori a 0°C creando uno strato fluido sul quale il ghiaccio scorre.

Esempio 4

Con un esperimento è possibile mettere in evidenza, tramite il fenomeno del rigelo, le conseguenze della pressione sul fenomeno della fusione.

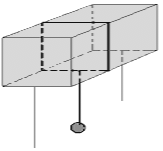
Su di un blocco di ghiaccio, a temperatura inferiore a 0°C, appoggiato a due sostegni, viene posto un filo di ferro ai cui estremi è applicato un grosso peso. Nei punti dove appoggia il filo la pressione è superiore a quella atmosferica per cui il ghiaccio fonde. L'acqua che si viene a formare dopo il passaggio del filo si trova ad una temperatura ambientale inferiore allo zero ed è sottoposta alla pressione atmosferica, non potendo rimanere quindi allo stato liquido solidifica subito dopo. Pertanto il filo attraversa tutto il ghiaccio e cade a terra lasciando unite tutte le parti del corpo.

Esempio 5

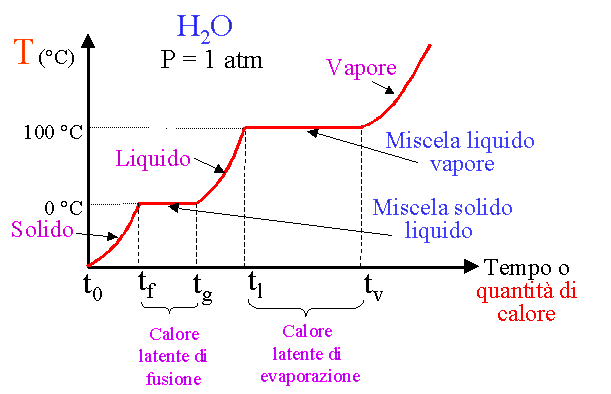
Analisi dei cambiamenti di stato di un sistema chiuso omogeneo formato da ghiaccio al quale viene applicato calore:

• -20°CÞ 0°C: il ghiaccio, pur trovandosi ancora in una fase solida, con l’aumento della temperatura si surriscalda. Pertanto si ha:

dove c_p è il calore specifico, cioè la quantità di calore necessaria per aumentare la temperatura di 1 Kg di acqua di 1 Kelvin.

• 0°C: pur continuando a fornire calore il sistema resta alla stessa temperatura per una certa quantità di tempo, che dipende dalla quantità di ghiaccio del sistema e dalla quantità di calore che gli viene fornita nell’unità di tempo. Questo è dovuto al fatto che siamo in presenza di un cambiamento di fase che non avviene in maniera istantanea.

c_l rappresenta il calore latente di fusione, è calore che non vedo (infatti non c’è aumento di temperatura) ma che devo somministrare affinché possa avvenire il passaggio.

• 0°CÞ 100°C: il ghiaccio è ormai acqua, che riprende ad aumentare di temperatura

• 100°C: nella fase di evaporazione avviene un altro passaggio di stato, quindi la sostanza necessita di energia per spezzare i legami molecolari e diventare vapore

Dopo di che il gas riprende ad aumentare temperatura.

Il diagramma più utilizzato è quello ottenuto dalla proiezione della superficie (p,v,T) sul piano pressione-volume.

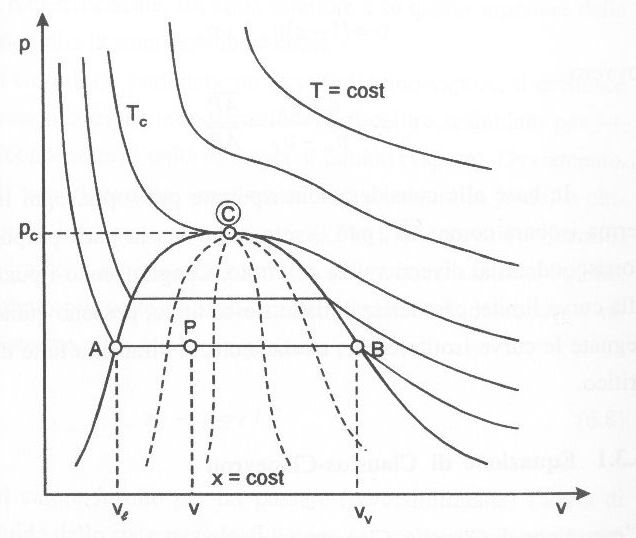
Fig. 6- Diagramma (p,v) dell’acqua

Nella diagramma (fig. 6), si nota bene come l’isoterma critica separi la zona dei vapori da quella dei gas. Inoltre, man mano ci si allontana da essa si va verso la zona dei GAS PERFETTI, dall’equazione di stato pari a

e per i quali non c’è possibilità di solidificazione o liquefazione, anche alterando la pressione.

Inoltre si individua la presenza di un’altra curva rilevante posta al di sotto di quella critica e passante anch’essa dal punto critico, chiamata campana di Andrews, all’interno della quale si trova la zona d’equilibrio L-V.

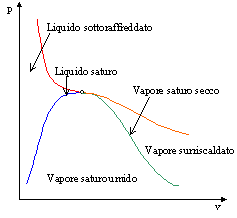
Fig. 7- Diagramma (p,v): sono evidenziate le zone in cui sono presenti i diversi stati della materia

Dal diagramma (p,v) si possono fare ulteriori distinzioni riguardo allo stato della sostanza (fig. 7):

• VAPORE SATURO UMIDO, all’interno della campana di Andrews. Indica la presenza di acqua e vapore d’acqua.
• LINEA DEL LIQUIDO SATURO, corrispondente alla curva limite inferiore che congiunge il punto triplo a quello critico. Rappresenta gli stati fisici in cui pur essendoci la presenza di fase L e V, è presente la sola fase liquida.
• LINEA DEL VAPORE SATURO SECCO, corrispondente all’altro ramo della campana, chiamato curva limite superiore, nel quale è presente solo vapore pur essendoci sia la fase liquida che quella aeriforme.
• VAPORE SURRISCALDATO, zona del vapore compresa tra la curva limite superiore e l’isoterma critica.
• LIQUIDO SOTTORAFFREDDATO, nella zona liquida compresa tra l’asse p e l’isoterma critica.

Va precisato che i termini ‘surriscaldato’ e ‘sottoraffreddato’ non indicano la temperatura, infatti, ad esempio, il vapore d’acqua contenuto nell’aria è un vapore surriscaldato pur essendo a temperatura ambiente.

All’interno della campana di Andrews le trasformazioni isoterme (a temperatura costante) sono anche isobare, cioè a pressione costante, per questo vengono rappresentate come segmenti paralleli all’asse v.

Se introduciamo una nuova grandezza, chiamata Titolo (x) definita come il rapporto tra la massa del vapore e la massa totale:

si otterrà un valore compreso tra 0 e 1

in particolare:

se X=0 Þ il punto si trova sulla curva limite inferiore (liquido saturo)

se X=1 Þ il punto si trova sulla curva limite superiore (vapore saturo secco)

Ogni linea isobara-isoterma può essere divisa in parti proporzionali che corrispondono ai diversi valori di titolo, potendo così individuare altre curve, definite curve isotitolo, che partendo dal punto critico congiungono tutti i punti aventi stesso titolo all’interno della campana (fig. 6- linee tratteggiate).

Grazie al concetto di titolo, che ci indica la percentuale delle componenti formanti il sistema, è quindi possibile studiare le zone di equilibrio in cui sono presenti due fasi.

Data la definizione di volume specifico (v/m) si ha che

si ottiene quindi:

potendo da questa ricavare un’altra equazione per il titolo:

dove

v_d rappresenta il volume differenziale, cioè il variare del volume specifico col passaggio di stato.

Si può infine scrivere il volume medio in funzione del titolo

Analogamente si possono ricavare le altre grandezze fisiche:

Energia interna Þ

Entalpia Þ

Entropia Þ