PROBLEMI DI TERMODINAMICA

Vi è una prima distinzione da fare nell’affrontare un problema di termodinamica:

1) se esso riguarda il vapore di acqua saturo

2) se invece coinvolge miscele di aria e vapore.

Grandezza fondamentale in entrambe i casi risulta essere il titolo X che si ottiene però in maniera diversa, in quanto per

1) X =

dove M_v rappresenta la massa del vapore, mentre M_tot è la massa totale. Quindi per esempio

M_v = 0.05 Kg

M_liq = 0.95 Kg

M_tot = 1 Kg

X =

Diversamente si ha per

2) X =

in cui M_a è la massa secca dell’aria e non quella totale. Dunque in questo caso

M_v = 5 kg

M_{a =} 100 kg

M_tot = 105 kg

X =

Possiamo notare come in questo secondo caso non via sia demarcazione netta degli elementi coinvolti come avveniva nell’iterazione tra liquido e vapore, ma vi è una miscela di aria e vapore. Proprio per questo motivo l’unità di misura del TITOLO X va qui lasciata indicata, non essendo semplificabile una massa di aria con una massa di vapore.

Poiché i dati degli esercizi variano a seconda del numero di matricola dello studente, di seguito verrà considerato per la risoluzione il numero di matricola 123456. Per avere i risultati utilizzando dati di ingresso differenti, si rimanda alla relativa tabella di Excel.

ESERCIZI DAL COMPITO DEL 1/02/2001 (PRIMO APPELLO)

1° Esercizio – Termodinamica

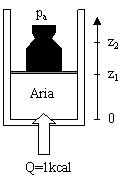
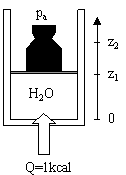
Aria secca è contenuta entro uno stantuffo, su cui grava la pressione atmosferica ed un peso avente massa M pari a 100+AB kg, che mantiene costante la pressione al suo interno. L’area dello stantuffo A è pari a 100+CD cm2. La temperatura iniziale T1 del fluido entro lo stantuffo è pari 20+EF °C. L’altezza iniziale dello stantuffo, z1, è pari a 100mm. Al fluido viene comunicata dall’esterno una quantità di calore Q pari ad 1 kcal. Il fluido si espande, sollevando il peso. Trovare:

- Altezza finale dello stantuffo z₂

- Temperatura finale T₂

M = 112 kg

A = 134 cm² = 0,0134 m²

T₁ = 76 °C

z₁ = 100 mm

Q = 1 kcal

P_a (pressione atmosferica) = 101.325 pa

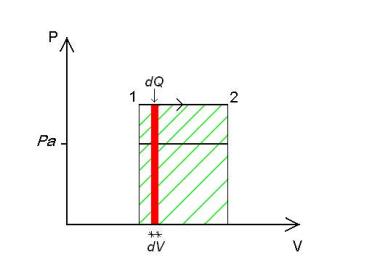
Il fatto fondamentale da considerare è, innanzitutto, che la trasformazione avviene a pressione costante, si ha cioè questa situazione

GRAFICO 1

P_tot = P_{a +}

V₁ ==

Utilizzando l’equazione di stato dei gas perfetti si ottiene inoltre:

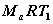
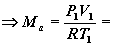
P₁V₁ = 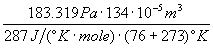= 0,002455 kg

dove si ricorda che P₁, V₁, T₁, rappresentano rispettivamente pressione, volume e temperatura allo stato iniziale, mentre R è una costante.

Dal primo principio della termodinamica sappiamo che

U₂ – U₁ = Q – L (1)

cioè che la variazione di energia interna del sistema è pari al lavoro L sottratto alla quantità di calore Q e inoltre dalla definizione di ENTALPIA che

(2)

Ma poiché il sistema passa dallo stato iniziale 1 a quello finale 2 tramite una trasformazione isobara (cioè a pressione costante) dalla (2) segue che

e da (1) si ottiene

(3)

dove c_p è la capacità termica a pressione costante. Possiamo ora ricavare T2 ricordando che 1kcal corrisponde a 4187 J:

= 1781.4 °C

e V₂:

da cui otteniamo l’altezza finale dello stantuffo

z_{2 =}

Vogliamo ora calcolare aggiuntivamente

a) il lavoro L compiuto per sollevare il grave

b) la variazione di entropia .

Per quanto riguarda il primo punto si ha già disponibile ogni dato:

0,589 m – 0,1 m = 0,489 m

L =

A questo punto, una verifica del lavoro L così ottenuto si può ottenere calcolando l’area del rettangolo sotteso al grafico della trasformazione (GRAFICO 1)

L = (V₂ -V₁) (P – P_a) =(0,007896 m³ – 0,00134 m³) (183319 pa – 101325 pa) = 537 J

Per ricavare la variazione di entropia ricordiamo invece la (3) e scriviamola sotto la forma

=

2° Esercizio – Termodinamica

Risolvere nuovamente l’esercizio n. 1, ma sostituendo vapore di acqua saturo all’aria secca. In questo caso non è assegnata la temperatura iniziale T1, ma è invece assegnato il titolo x1, che vale 0.1+F/40. Trovare:

- Altezza finale dello stantuffo z2

- Titolo finale x2

x1=

M = 112 kg

A = 134 cm² = 0,0134 m²

T₁ = 76 °C

z₁ = 100 mm

Q = 1 kcal

P_a (pressione atmosferica) = 101325 pa

Consideriamo inizialmente che, trattandosi di vapore di acqua saturo, il fatto di avere pressione costante ci permette di conoscere, tramite le tabelle, anche la relativa temperatura di saturazione; abbiamo infatti

P= 183319 pa T_sat= 117 °C

siamo cioè di fronte ad una trasformazione sia ISOBARA che ISOTERMA. Se ricordiamo ora la (3), sappiamo che

H₂ – H₁ = Q = 4187 J

e che per calcolare l’entalpia specifica possiamo considerare la relazione

h_x = h_L + xh_d

in cui h_L e h_d rappresentano rispettivamente l’entalpia specifica dell’aria secca e l’entalpia specifica del vapore d’acqua e x il titolo.

Si ottiene quindi che

4187 J (4)

Poiché in questo caso non vi è aria secca, h_L2 e h_L1 sono nulli; inoltre è dato il titolo x1, mentre rimangono incognite l’entalpia h_d che possiamo conoscere attraverso le tabelle e pari a 2211 e M_H2O che si può ricavare dalla formula per il calcolo del volume specifico:

(5)

Ma v₁ si ottiene anche dalla relazione che lo lega al titolo x1; tramite le tabelle si ha così che

(6) = 0,001058 + 0,25

e sostituendo questo valore in (5) dove V₁ era già stato calcolato nel primo esercizio si ottiene

M_H2O= = 0,007512 kg

Si è ora in grado di ricavare da (4) il titolo x2 :

x2 = x1 + = 0.502

Ricaviamo ora il secondo volume specifico v₂ nello stesso modo di (6)

v₂ = 0,001058 + 0,502

V₂ = m³

A questo punto abbiamo tutti gli elementi per ottenere l’altezza z₂ finale dello stantuffo:

In aggiunta a quanto richiesto dal problema si voglia calcolare anche

- il lavoro compiuto L

- la variazione di entropia

Per quanto riguarda il primo punto, abbiamo già tutti gli elementi a disposizione, ricordando che è possibile ottenere il lavoro tramite la relazione

112kg109,87 J

dove si ricorda che g rappresenta l’accelerazione di gravità.

Ricordando che la variazione di entropia è pari a

(7)

rimane da determinare solo l’entropia differenziale S_d, ottenibile da

S_d =

Quindi dalla (7) si ha che

ESERCIZIO DAL COMPITO DEL 28/02/2001 (SECONDO APPELLO)

3° Esercizio – Termodinamica

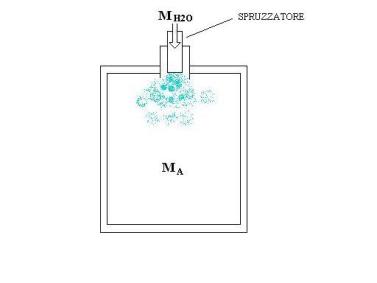
Entro un ambiente di volume V pari a 100+CD m3 si trova aria umida con temperatura T1 pari a 20+E °C ed umidità relativa pari a 30+F %. Nell’ambiente viene introdotta un massa di acqua M_H2O, alla temperatura T1, cosicché l’umidità cresce ad un valore pari a 60+F %. Ovviamente la temperatura cala, mancando qualsiasi apporto di calore esterno. Determinare:

- Massa di aria secca contenuta nell’ambiente

- Massa di acqua M_H2O da aggiungere

V= 134 m³

T₁= 25 °C

36% = 0,36

66% = 0,66

Consideriamo innanzitutto che questo problema riguarda due categorie: una prima che coinvolge la sfera dei gas perfetti ed una seconda che si riferisce alle miscele di aria e vapore. Per calcolare infatti la massa d’aria secca contenuta inizialmente nell’ambiente, basta ricordare l’equazione di stato dei gas perfetti nella forma

(8)

Ricavando la pressione iniziale P₁ tramite il prodotto tra il grado igrometrico iniziale e la pressione di saturazione P_sat (il cui valore è noto dalle tabelle) ,si ha che

P₁ =

e si può ottenere di conseguenza anche la pressione parziale P_a tramite la legge di Dal ton, infatti

P_tot = 101325 pa =P_a + P₁ 101325 pa – 1141 pa = 100184 pa

Si è così in grado di ottenere la massa di aria secca M_a dalla (8)

M_a =

Si prenda ora in considerazione il diagramma psicrometrico relativo al problema, che riporta le temperature sull’asse delle ascisse, il titolo x sulle ordinate e sulle linee curve l’umidità relativa in percentuale:

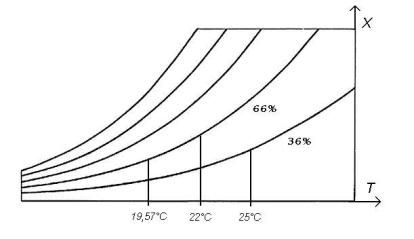
Come si può facilmente vedere, vi è una relazione che lega il titolo x al grado igrometrico, infatti:

x1 = (9)

in cui P_tot rappresenta, in questo caso, la pressione atmosferica e P_s la pressione di saturazione del vapore alla temperatura considerata (25°C), valore che si ricava dalle tabelle. Si hanno ora gli elementi per calcolare l’entalpia specifica dell’aria umida

(10)

dove compaiono il calore di vaporizzazione dell’acqua r_o=2500 ed il calore specifico del vapore d’acqua c_p,v= 1,9. Per ottenere la massa d’acqua introdotta M_H2O occorrerebbe ora il titolo incognito x2 in quanto

M_H2O = M_a (11)

ma tale titolo, come sappiamo dalla (9) è legato alla pressione di vapore saturo alla temperatura T₂, anch’essa incognita. Procediamo allora per tentativi ipotizzando una temperatura T₂ alla quale corrisponderà una pressione di saturazione P_s ottenibile dalle tabelle. L’attendibilità di questa prima ipotesi potrà poi essere verificata in seguito.Cominciamo col considerare una temperatura T₂ = 22°C e di conseguenza una pressione P_s pari a 0,02642ba; il titolo x2 ricavato tramite la (9) sarà dunque:

x₂ =

In base a quanto ricavato la massa d’acqua introdotta risulta dalla (11)

M_H2O =

Occorre però, a questo punto, accertarsi di essere giunti ad un valore verosimile; per farlo ricordiamo la (10) e riscriviamola nella forma

(12)

Si nota come l’unica incognita in tale equazione sia l’entalpia specifica J₂; ottenendola con un’altra relazione potremo poi sostituirla nella (12) e confrontare il valore della temperatura T₂ così ottenuta, con quella che avevamo inizialmente ipotizzato di 22°C. Per fare ciò prendiamo ora in esame la definizione di entalpia che mette in relazione la variazione di entalpia e la variazione di energia interna:

(13)

ma poiché l’energia, e di conseguenza l’entalpia è conservata, la (13) rimane così formulata

(14)

Scrivendo H₂ tramite l’entalpia specifica J_2, si ha che

e allo stesso modo

dove h_L rappresenta l’entalpia specifica dell’aria umida. In questo modo la (14) diventa

(15)

Si può ottenere il valore di h_L tramite il calore specifico dell’aria C_L e la temperatura T₁:

h_L =

Abbiamo a questo punto tutti gli elementi per ricavare dalla (15) l’entalpia specifica

J₂ =

Andando a sostituire questo valore nella (12) notiamo però che:

T₂ =

Risulta cioè una temperatura che si discosta sensibilmente da quella ipotizzata di 22°C. Questo significa che si è scelto un valore eccessivo ed occorre perciò considerare una nuova temperatura T₂ che sia in grado di fornire, in questa verifica, un valore più verosimile. Si verifica (*) che tale attendibilità si raggiunge assumendo una temperatura T₂ di circa 19,57°C, dalla quale si ricava per la (11) una massa d’acqua pari a

M_H2O =

in cui il titolo x2 è sempre ottenibile dalla (9). In questo caso si ha infatti l’entalpia specifica J₂ pari a

J₂ =

e riotteniamo una temperatura T₂ uguale a

T₂ =

(*) Per la verifica si rimanda alla relativa tabella di Excel