FRIGERI SIMONE MATR.
139735
Lezione di Fisica-Tecnica del 13/12/2001 ore 14.30-16.30
ESERCIZIO SUI CICLI FRIGORIFERI
Tramite il seguente esercizio relativo ad un ciclo
frigorifero, sarà possibile comprendere quali grandezze entrano in gioco in
questo tipo di macchine.
Un impianto frigorifero classico può essere
schematicamente rappresentato nel seguente modo:
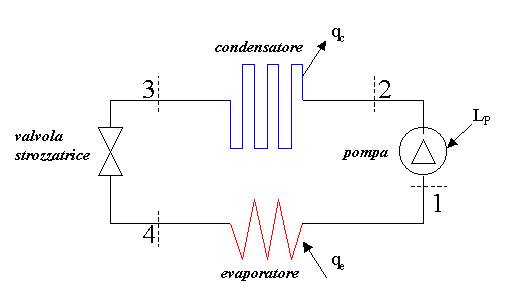
Tale macchina ha lo scopo di sottrarre calore ad un
ambiente, trasportando il calore assorbito in un diverso ambiente a temperatura
più elevata. Il refrigerante utilizzato nel seguente esempio è il Freon12, un
gas che non gela alle temperature inferiori allo zero. Utilizzato nei vecchi
frigoriferi, ora questo gas è considerato fuori legge a causa dei problemi
ambientali da esso derivati. Nei frigoriferi moderni vengono utilizzati diversi
gas che mantengono però caratteristiche simili a quelle del Freon12.
Viene ora fornito il diagramma del Freon12 in
funzione della temperatura (T) e dell’entalpia specifica (s):
Analizziamo ora il percorso del fluido attraverso i
vari componenti dell’impianto, studiando i processi che ne determinano dal
diagramma sopraindicato.
Passaggio:
1-2: Il gas passa attraverso ad
un COMPRESSORE, che gli fornisce lavoro (Lp). In questa parte
avviene una compressione adiabatica reversibile a entalpia costante, si innalza
la temperatura e il gas diventa liquido a causa della forte pressione a cui è
sottoposto. Nel grafico si ha un innalzamento della temperatura, mentre
l’entalpia rimane costante.
2-3: Attraverso il CONDENSATORE,
viene sottratto calore al fluido (qc). Tramite una trasformazione a
pressione costante, il gas raffreddato condensa totalmente. Nel grafico si ha
l’andamento di una isobara al di fuori della campana, mentre la condensazione
completa è rappresentata dalla linea orizzontale all’interno della campana,
fino alla curva limite inferiore.
3-4: Il freon attraversa una VALVOLA
STROZZATRICE, che fa espandere il gas; ciò produce la diminuzione della
pressione e l’abbassamento della temperatura del fluido. Questa trasformazione
è irreversibile e comporta l’aumento di entropia, ma nel grafico si semplifica
considerando un andamento verticale.
4-1: L’EVAPORATORE in
seguito, vaporizza il fluido, trasformandolo, grazie ad una operazione isoterma
e isobara, dallo stato liquido allo stato gassoso. Consente al fluido di
assorbire il calore all’interno del frigorifero. In questa fase si ha l’effetto
refrigerante richiesto.
Si conclude così il ciclo frigorifero, che può
essere reso continuo fornendo costantemente energia alla pompa.
Sapendo che le pressioni a monte e a valle del
compressore sono 3,6 bar e 9,6 bar e avendo a disposizione il diagramma del
freon12, si ricavano punto per punto i valori energetici specifici del fluido,
che si possono riportare nella seguente tabella.
|
|
P |
t |
h
(kj/kg) |
|
1 |
3.6 bar |
5°C |
353.611 |
|
2 |
9.6 bar |
50°C |
371.07 |
|
3 |
9.6 bar |
40°C |
288.53 |
|
4 |
3.6 bar |
5°C |
238.52 |
RENDIMENTO
FRIGORIFERO
Volendo calcolare il rendimento hf, si dovrà calcolare qe, cioè il calore sottratto dall’evaporatore, e l c , ovvero il lavoro speso dal compressore.
Infatti ricordiamo che:
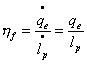
mentre le formule per il condensatore e il
compressore sono rispettivamente:
![]()
e
![]()
Sostituendo i valori appena ricavati ottengo:
![]()
MACCHINA DI CARNOT
Confrontando il valore
trovato con quello ideale che sarebbe stato ottenuto utilizzando una macchina
di Carnot (che utilizza un gas perfetto e funziona tenendo in considerazione le
due temperature massime e minime di evaporazione e condensazione) otteniamo
che:
![]()
Siccome hf <hc significa
che la nostra macchina non è ideale.
COMFORT
TERMOIGROMETRICO
Per comfort termoigrometrico
si intende la sensazione di benessere fisico che la persona avverte
soggiornando in un ambiente. Naturalmente tale sensazione è soggettiva, cioè
non è possibile ottenere un comfort assoluto, pertanto si tende di riprodurre
una situazione piacevole per il maggior numero di persone.
Il primo parametro
indispensabile per rendere confortevole un ambiente è sicuramente la
temperatura, ma non è sufficiente. Avere una temperatura, infatti, di 20 °C
all’interno di un ambiente non significa
necessariamente che questo sia più o meno confortevole. Se ci troviamo
ad esempio in una sauna, per quanto la temperatura non sia molto alta, la
sensazione è di spiacevolezza dal momento che, essendo l’umidità,
contrariamente, molto elevata, percepiamo estremo caldo. Se, invece, ci
troviamo al mare alla stessa temperatura, ma in condizione di brezza e aria
molto secca, la sensazione è di un ambiente piacevole, o addirittura fresco.
Dunque, è possibile intuire
come non basti determinare soltanto la temperatura, ma anche l’umidità.
La casistica è anzi più
complessa perché occorre accertarsi della funzione del locale e
conseguentemente dell’abbigliamento indossato dalle persone che questo
accoglie. Comprendiamo ciò se per esempio paragoniamo una palestra con un
ospedale: nella prima la temperatura può essere più bassa perché facendo
attività fisica il nostro corpo produce calore mentre nel secondo, ove ci sono
delle persone malate e in situazioni disagevoli, con la stessa temperatura si
potrebbe addirittura percepire freddo.
Quindi, solo considerando la
funzione del locale, l’attività svolta e l’abbigliamento tenuto in questo, si
potranno stabilire gli intervalli di temperatura e di umidità che rendono la
vita al suo interno sana e piacevole.
E’ certo comunque che non si
potrà mai raggiungere una situazione di comfort totale, ovvero valido per
tutti, dal momento che il cambiamento di percezione varia da persona a persona.
Esistono centinaia di tabelle empiriche, ricavate da
teorie più o meno efficaci e fantasiose e da rilievi sperimentali, che
suggeriscono valori di temperatura e umidità che garantiscono una buona
abitabilità. La maggior parte di queste teorie si basa sull’idea di corpo umano
come sistema aperto che scambia calore con l’esterno e contemporaneamente
produce energia. Pertanto la sensazione
di comfort è assicurato entro una determinata fascia di scambio termico.
Viene ora data l’equazione
del corpo umano:
![]()
dove:
M = è l’energia prodotta dal
nostro metabolismo; Si misura in watt ed è l’unico positivo nella formula.
Altre energie sono negative perché abbandonano l’organismo per una serie di
trasferimenti di energia meccanica e termica.
Lp = è l’energia
utilizzata per l’attività polmonare molto dispendiosa, che cede energia
meccanica nell’aria;
Lg = è l’energia
utilizzata per svolgere lavoro contro le forze esistenti ( come la forza di
gravità). Si parla di meccanismo dell’erogazione : quando un muscolo
eroga energia brucia O2 , quando rientra nel corpo non viene
riconvertita in energia, ma dissipata in calore che scalda il muscolo.
U = è l’energia accumulata
nel nostro organismo;
Ed = è il calore
disperso per evaporazione dei pori (sudorazione a pelle secca);
Es = è il calore
disperso per evaporazione del sudore dalla pelle;
Ed – Es =Ws
: identifica la
sudorazione massima e minima.
Er = Vs = è il
calore disperso con la respirazione;
R + C = è il calore scambiato dalla
superficie esterna del corpo umano con l’ambiente per irraggiamento e convezione.
L’unico fattore su cui può
agire il corpo umano per termoregolarsi è la sudorazione. Se un ambiente quindi
è saturo, il nostro sudore non potrà evaporare perché l’aria sarà già piena di
tutto il vapore acqueo disponibile, il nostro meccanismo di regolazione sarà
impedito e dovrà aumentare maggiormente la sudorazione.
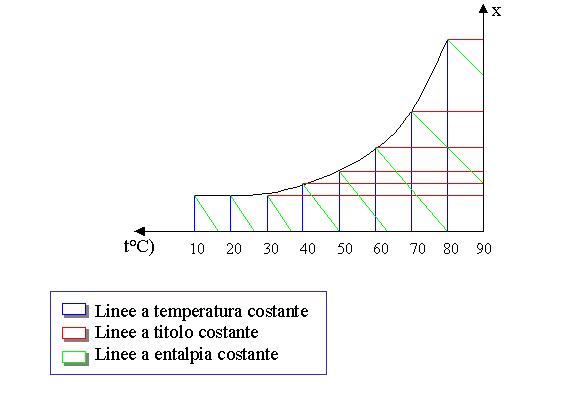
Per definire meglio il comfort,
ci si può avvalere dei diagrammi psicrometrici, dove vengono riportate la
temperatura (sull’asse x) e il titolo (sull’asse y), che serve per definire
l’umidità. Eccone un esempio:
DIAGRAMMA PSICROMETRICO
ESERCIZIO
SULLE MISCELE D’ARIA E VAPOR D’ACQUA
Data aria umida alla temperatura di 30°c con umidità
φ =0,6 e pressione p =1bar, determinare titolo X e pressione parziale del
vapore pv.
Dalla definizione di umidità relativa:
![]()
Identificando
con Mv e Mvs
rispettivamente la massa del vapore e la massa del vapore in
saturazione e con mv, e mvs il numero
di moli del vapore e il numero di moli del vapore in condizione di saturazione.
Poiché i vapor d’aria e d’acqua sono assimilabili ad
un gas perfetto, si può considerare l’equazione ad esso relativa:
![]()
Dove V è il volume del vapore, R è la
costante universale dei gas e Τ è la temperatura assoluta. In condizioni
di saturazione si ottiene:
![]()
Si riscrive il rapporto tra le moli in termini di
pressione, volume e temperatura, ricavandolo dall’equazione dei gas e si ottiene:
![]() quindi
quindi ![]() ← ricavato dai
diagrammi
← ricavato dai
diagrammi
↓
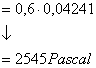
Si deve ricavare il titolo ![]()
Mv = massa del vapore.
Ma = massa dell’aria.
μv = massa molare del vapore; è un
valore noto pari a 18 kg/kmol.
μa = massa molare dell’aria; è un
valore noto pari a 29 kg/kmol.
ηa = numero di moli dell’aria.
Le pressioni del vapore e dell’aria sono parziali,
perciò la loro somma risulta essere la pressione totale dell’ambiente ![]() . Quindi ricavando algebrica-mente pa e andando a
sostituire:
. Quindi ricavando algebrica-mente pa e andando a
sostituire:
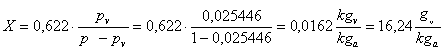
kgv = kg di vapore; kga = kg d’aria secca.
ESERCIZIO SULLE MISCELE D’ARIA E VAPOR D’ACQUA
Calcolare i valori del
flusso in uscita in un miscelatore ove si ha una semplice miscelazione senza
scambio di calore e umidità in cui entrano due flussi d’aria in condizioni
differenti. Sono note la pressione di 1 bar, la portata in massa di aria della
prima e della seconda corrente, rispettivamente pari a M1a
= 400 kg / h e M2a = 800 Kg / h, la temperatura del
primo e del secondo flusso, pari a t1 = 32 °C e t2 = 26
°C e le rispettive umidità relative f1= 0.8 e f2 = 0.5.
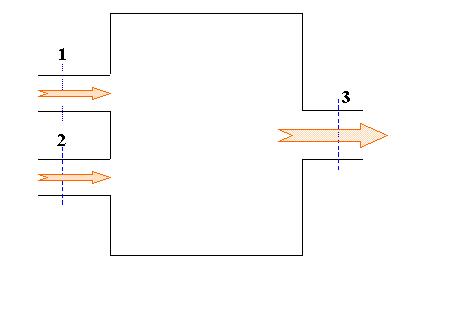
Dati del problema:
p = 1 bar
M1a = 400Kg/h
t1 = 32°C j1= 0.8
M2a = 800 Kg/h
t2 = 26°C j1= 0.5
All’interno del miscelatore avviene una semplice
miscelazione senza scambio di umidità e calore.
Come in tutti gli esercizi
di miscelazione, si considera il bilancio in termini di massa ed energia e con
la legge di conservazione sia della massa d’aria che della massa d’acqua
(quindi della massa totale) si definiscono le grandezze d’entrata e d’uscita.
Quindi dal bilancio, la portata in massa d’aria in 3 è:
![]()
Per il bilancio in massa del
vapor d’acqua si può scrivere la medesima equazione, poiché l’acqua entra
sottoforma di vapore sia nel punto 1 che nel 2 e sempre come vapore esce dal
punto 3, quindi si conserva la portata oraria del vapore.
![]()
Per la definizione di titolo
si ricava che:
![]()
infatti il titolo è uguale al rapporto tra la portata in massa del vapore e quella dell’aria sia in termini specifici che orari; perciò si può riscrivere l’equazione:
![]()
Dopo aver ricavato i titoli in funzione
dell’umidità relativa, si può scrivere il titolo assoluto (X, che indica quanti
sono i grammi di vapor d’acqua in ogni kg d’aria), in funzione dell’umidità
relativa che indica quanto manca alla condizione di saturazione.
![]()
Ricavo i singoli valori di x1
e x2:
![]()
![]()
In particolare date le temperature t1 e t2
si ricavano rispettivamente p1v,s =0,4753 e p2v,s
=0,0336.
Ora che abbiamo ottenuto i titoli X1 e X2
e le portate in massa d’aria, si può calcolare il titolo X3 dall’equazione
della conservazione della portata in massa dell’aria:
![]()
Si poteva ottenere ciò molto
facilmente anche per via grafica: conoscendo il punto 1 e il punto 2 è possibile determinare il punto 3 in quanto è la media pesata in
funzione dei titoli e delle temperature. Si rappresentano le due situazioni
termodinamiche all’ingresso dei due condotti e si ricava con i dati la
situazione d’uscita. Questa dovrà risultare su un segmento congiungente i due
punti d’ingresso.
L’entalpia specifica non
varia all’interno del miscelatore, cioè il flusso di entalpia in uscita è
uguale al flusso di entalpia in entrata.
Infatti Dh = q – l = 0 perché
all’interno del miscelatore lo scambio di calore (q) è nullo così come il
lavoro (l).
Quindi si può scrivere la legge di conservazione
dell’energia sottoforma di entalpia e ricavare facilmente J3.
LEGGE DELLA CONSERVAZIONE
DELL’ENERGIA SOTTO FORMA DI ENTALPIA.
![]()
da cui:
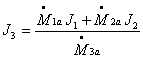
Per ricavare J1 e J2 è sufficiente
applicare la formula ricavata dalla teoria:
![]()
![]()
![]()
Sostituendo i valori trovati
nell’equazione, si ottiene così:
![]()
Si può scrivere J3
in funzione delle altre grandezze e ricavare algebricamente t3:
![]()
![]()
Si scrive X3 in
funzione dell’umidità relativa φ3 :
![]()
dalle tabelle di riferimento
si ottiene che ![]()
ricavando infine:
![]()