Per rendere chiara e comprensibile questa relazione occorre, dal mio punto di vista, cercare di completare il discorso con quelle nozioni, forse scontate o "palesi" ma essenziali al fine della comprensione, che distinguono una sequenza meccanica di formule da una lettura semplice , senza che siano però trascurate le difficoltà reali.

Definizione:

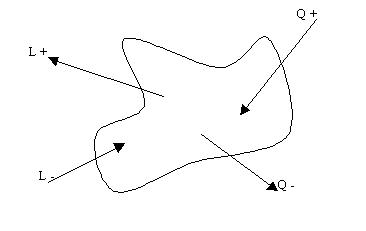
Sistema: si definisce sistema S una regione dello spazio delimitata da una linea di confine che può essere chiusa (e in tal caso si parlerà di sistema chiuso), oppure aperta (e quindi si chiamerà sistema aperto).

Fino ad ora abbiamo affrontato lo studio delle leggi della termodinamica limitandoci a considerare i sistemi chiusi.

Definizione: Sistema chiuso

Una determinata regione di spazio delimitata da una superficie, reale o apparente, rigida o deformabile, che ne costituisce il confine e ha la proprietà di essere chiusa, ovvero di impedire qualsiasi scambio di materia con l’esterno. La massa di un sistema chiuso è quindi costante e non cambia nel tempo: se potessimo marcare le molecole presenti nel sistema ad un dato istante, queste rimarrebbero sempre le stesse anche dopo un tempo t arbitrario e indipendentemente dalle trasformazioni subite dal sistema stesso.

In realtà, come già sappiamo dallo studio del primo Principio della termodinamica, la Teoria della relatività di Einstein lega la variazione di massa alla variazione di energia.

Ricordiamo:

Definizione: Il primo principio della termodinamica

Il primo principio è dunque un principio di conservazione dell'energia. Esso afferma che, poiché l'energia non può essere né creata né distrutta, la somma della quantità di calore ceduta a un sistema e del lavoro compiuto sul medesimo deve essere uguale all'aumento dell'energia interna del sistema stesso. Calore e lavoro sono i mezzi attraverso i quali i sistemi si scambiano energia.

In ogni macchina termica una certa quantità di energia viene trasformata in lavoro; non può esistere nessuna macchina che produca lavoro senza consumare energia. Una simile macchina, se esistesse, produrrebbe infatti il cosiddetto "moto perpetuo di prima specie".

Il primo principio è valido anche in caso di interazioni nucleari, infatti, in questi casi, solo in apparenza si osserva la creazione di energia dal nulla; in realtà la teoria della relatività formulata da A. Einstain (Ulma 1879 - Princeton, New Jersey 1955) ha esteso il principio della conservazione dell’energia in un principio di conservazione dell’energia e della massa esprimibile secondo la celebre relazione:

dove:

è la velocità della luce.

N.B.: Nello studio da noi condotto trascuriamo quanto sostenuto dalla Teoria della relatività di Einstein in quanto, avendo un elevato coefficiente di proporzionalità, ad una sensibile variazione di energia corrisponde un’irrilevante variazione di massa.

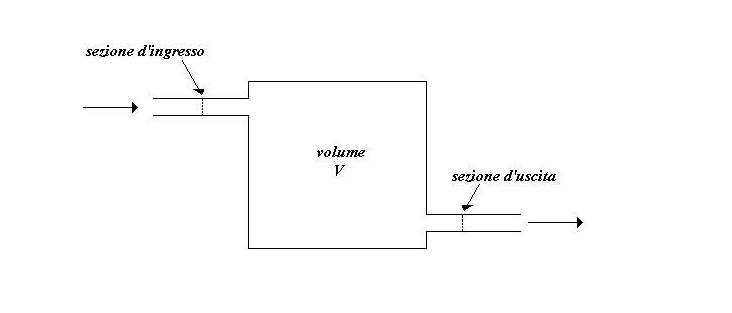
Considereremo dei sistemi aperti semplici che presentano una sola sezione d’ingresso e una sola sezione d’uscita a massa costante, cioè la stessa quantità di massa che entra deve anche uscire.

Ciò che consideriamo è allora un sistema aperto stazionario in cui anche la temperatura, la pressione, il volume e i flussi del sistema devono essere gli stessi in ogni istante di tempo.

La stazionarietà del sistema non è una caratteristica di tutti i sistemi aperti, può però essere realizzata, in casi particolari attraverso opportuni sistemi di controllo. Un esempio di sistema aperto stazionario è un impianto termoelettrico.

Sara’ possibile poi estendere le relazioni che troveremo anche al caso di sistemi aperti con più sezioni di ingresso e più sezioni di uscita.

Vogliamo ora approfondire , dopo una breve ma essenziale introduzione, il nostro discorso dando la definizione ufficiale per i sistemi aperti e ricavando per essi le equazioni di bilancio della massa e dell’energia. La maggior parte dei problemi termotecnici richiede infatti l’applicazione dei principi della termodinamica a sistemi che scambiano in continuazione materia con l’esterno: tutte le apparecchiature che sono interessate da un flusso di materia rientrano nella categoria dei sistemi aperti.

Definizione: Sistema aperto

Un determinato volume dello spazio racchiuso da una superficie, detta confine del sistema, attraverso la quale può’ entrare o uscire una certa quantità di materia. Il confine e il volume in esso racchiusi non variano nel tempo.

Si considerano trasformazioni del sistema aperto tutti i fenomeni che avvengono in questo volume anche se questi comportano un flusso di massa attraverso di esso.

Generalmente si definisce il volume che costituisce un sistema aperto facendo riferimento a superficie di confine fisiche: in tal modo la materia non può indistintamente entrare o uscire da ogni punto di esse.

La maggior parte della superficie di confine di questo sistema è impermeabile al flusso di materia, presenta però alcune zone, dette sezioni d’ingresso, attraverso le quali la materia può entrare e alcune zone, dette sezioni d’uscita, attraverso le quali la materia può uscire, queste vengono quindi realizzate attraverso una superficie permeabile.

Fig. 1: schematizzazione di un sistema aperto con una sezione di ingresso ed una sezione di uscita..

E’ possibile utilizzare i metodi di indagine termodinamica, già elaborati per il sistema chiuso, anche per l’analisi del sistema aperto. Per fare ciò è sufficiente considerare un sistema chiuso, che chiameremo ausiliario, che si sposta nello spazio per un certo intervallo di tempo, e contemporaneamente una regione, fissa nello spazio, che nel tempo viene attraversata dallo stesso sistema chiuso: questa regione costituisce appunto il sistema aperto. Le variabili che servono per descrivere un sistema aperto sono esprimibili in funzione della posizione e del tempo.

Equazione di bilancio di massa:

Valutiamo la massa del sistema aperto al tempo , troviamo:

(2)

Successivamente, trascorso il tempo Dt , misureremo al tempo t+Dt una massa pari a :

(3)

Per affrontare lo studio di un sistema aperto ci serviremo anche di un sistema chiuso ausiliario a massa costante definito in maniera tale da comprendere (all’istante iniziale ) tutta la massa contenuta nel sistema aperto ed in più una porzione di massa collocata immediatamente a monte della sezione 1 d’ingresso del fluido.

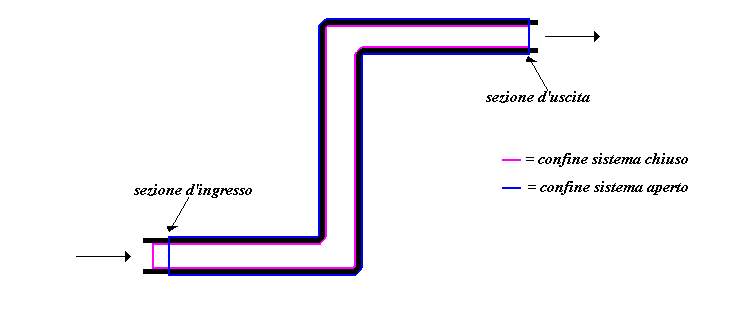
Fig.2: Sistema aperto all’istante iniziale

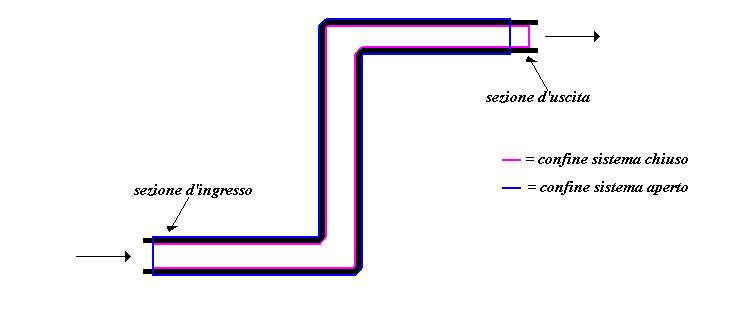
Fig. 3: Sistema aperto all’istante finale

Nel sistema chiuso ausiliario troviamo al tempo una massa di:

(4)

a al tempo una massa di:

(5)

Solitamente si ha che:

(6)

questa disuguaglianza diviene però un’uguaglianza se ci troviamo a studiare un sistema in regime permanente, cioè un sistema in cui entra una quantità di massa pari a quella che esce.

Considerando il sistema chiuso, che è a massa costante per definizione, possiamo uguagliare la (4) e la (5):

(7)

Dividendo termine a termine per :

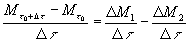(8)

Dalla definizione di derivata al tendere di Dt a zero abbiamo:

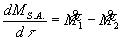(9)

Avendo definito: la massa del sistema aperto e le portate in massa

, ,

ed avendo considerato positive le portate in massa entranti nel sistema e negative quelle

uscenti. In generale, se la massa entra ed esce da più sezioni abbiamo:

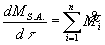(10)

Se oltre a poter trascurare gli effetti relativistici, siamo anche in presenza di m componenti che non reagiscono fra loro, l’equazione (10) degenera in m equazioni; in questo caso bisogna specificare che abbiamo m equazioni indipendenti e non m+1, perché una è esprimibile tramite le rimanenti m.

Per arrivare a scrivere un’equazione di bilancio dell’energia indichiamo convenzionalmente positivo il lavoro fatto dal sistema sull’ambiente, e positivo il calore fornito dall’ambiente al sistema. Solitamente il lavoro scambiato fra sistema aperto ed ambiente è dato dalla rotazione di un albero dovuta al passaggio del fluido, se è il sistema a compiere lavoro, o ad un motore se è l’ambiente a compiere lavoro.

Fig. 4: schematizzazione del lavoro scambiato fra sistema ed ambiente.

Valutiamo l’energia all’istante iniziale e all’istante finale, considerando anche forme d’energia come quella potenziale e cinetica che erano state supposte trascurabili per i sistemi chiusi.

Indicando con , , , rispettivamente le energie specifiche cinetica, potenziale ed interna abbiamo che all’istante la massa contiene un’energia pari a :

(11)

la massa un’energia: .

All’istante la massa ha un’energia:

(12)

la massa un’energia: .

Solitamente non sono specificate le energie contenute in ed in perché non ci interessa sapere che tipo di energie siano.

Dobbiamo relazionare in funzione della variabile temporale anche i flussi di lavoro e di calore, per cui abbiamo che il lavoro ed il calore scambiati in Dt saranno rispettivamente:

(13)

(14)

ove si è indicato con la potenza meccanica e con la potenza termica.

Ora ci manca da calcolare il lavoro di "pompaggio" del fluido in entrata ed in uscita, perché in effetti il sistema chiuso si è deformato nel lasso di tempo trascorso fra l’istante iniziale e l’istante finale della nostra osservazione.

Allora poiché:

(15)

(16)

e poiché l’equazione di bilancio di energia per un sistema chiuso afferma:

(17)

si ha:

(18)

Nella sovrastante equazione si è tenuto conto che è data dalla somma dell’energia contenuta nella massa e più il lavoro di "pompaggio" del fluido verso l’interno del sistema aperto ed è la somma dell’energia contenuta in e più il lavoro di "pompaggio" verso l’esterno; inoltre si è sostituito ad e rispettivamente l’equazione (13) e (14).

Ora ricordando che:

(19)

(20)

sostituendo la (19) e la (20) nell’equazione (18) e dividendo termine a termine per otteniamo:

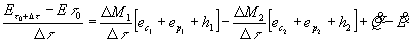(21)

facendo tendere a zero:

(22)

ove indica l’energia del sistema aperto.

Se ci troviamo nella situazione di regime permanente:

(23)

quindi l’energia del sistema aperto è costante; inoltre in questa particolare condizione:

(24)

Cioè vale:

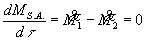
(25)

l’equazione di bilancio dell’energia in regime permanente risulta quindi essere:

(26)

ove: ;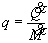

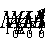
Si noti che tutti i termini dell’equazione (26) sono energie specifiche pertanto misurabili in J/kg.

Generalmente si incontrano delle difficoltà nel calcolare l’energia potenziale e quella cinetica perché di solito non sono costanti lungo la sezione del sistema salvo che in casi particolarmente semplici, mentre per l’entalpia resta valido il metodo usato per calcolarla attraverso le tabelle.

Per un corpo rigido vale:

(27)

ma un fluido non è un corpo rigido in movimento, per cui si definisce la velocità media W come quel valore ipotetico della velocità parallelo all’asse del condotto che, uniforme su tutta la sezione normale S sarebbe in grado di dare la stessa portata in volume che si ha nella realtà.

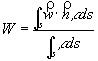(28)

Se la densità r è costante:

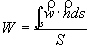(29)

Inoltre abbiamo che:

(30)

Con r costante:

(31)

ove è la portata in volume.

Quindi:

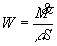(32)

La velocità media è però un cattivo indicatore per l’energia cinetica poiché scrivendo

(33)

non teniamo conto dei contributi dovuti alle componenti della velocità fuori asse che si presentano nei liquidi con moti vorticosi e del fatto che il quadrato del valore medio è minore del valore medio dei quadrati.

Per questo motivo si introduce un coefficiente correttivo a>1 per cui:

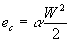(34)

Il coefficiente a è di difficile determinazione, fatta eccezione per alcune particolari situazioni:

• se siamo in presenza di un fluido avente un profilo di velocità parabolico di Poiseville, si riscontra: a=2. Tale valore di a è ritenuto un tetto superiore perché è molto difficile ottenere un moto laminare di Poiseville;
• se abbiamo un moto rigido, ove cioè un piccolo strato di fluido sul bordo della conduttura ha moto relativo ed il corpo centrale del fluido si muove rigidamente, allora: a=1;
• se abbiamo un moto fortemente turbolento ove la velocità media è pressoché costante a causa della viscosità del fluido allora si trova: a=1.

1. b)

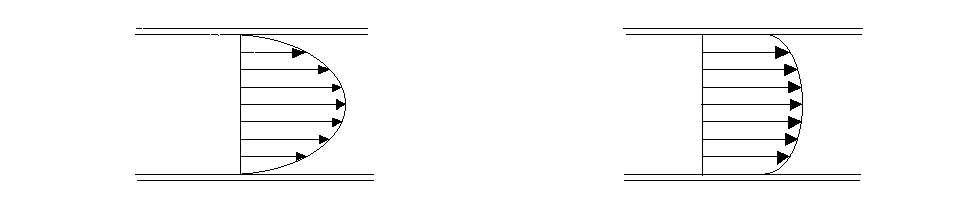
Fig. 5: profili di velocità per fluido in moto : a) laminare; b) turbolento

Possiamo quindi esprimere l’energia cinetica specifica come:

(35)

L’energia potenziale di un corpo si esprime:

(36)

Poiché si pone per semplicità nell’equazione (35) , possiamo scrivere l’equazione di bilancio dell’energia nella seguente forma:

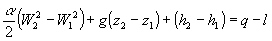(37)

Se l’energia cinetica e quella potenziale sono trascurabili, allora la (37) diviene:

(38)

Una caldaia produce vapore alla pressione di 40 bar e alla temperatura di 300 ^oC.

Supponendo che il sistema parta da una temperatura iniziale di 60 ^oC, calcolare la quantità di calore necessaria per vaporizzare una massa M pari ad 1 kg di acqua.

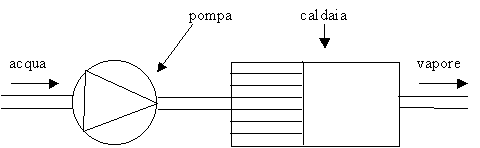
Fig.1-schematizzazione di una caldaia

La caldaia è una macchina che funziona prendendo in ingresso dell’acqua allo stato liquido e producendo in uscita del vapore surriscaldato.

In base ai dati che vengono forniti e sapendo che il processo compiuto dalla caldaia è a pressione costante, si ha che le condizioni iniziali e finali sono rispettivamente: T₁ = 60 ^oC, P₁ = 40 bar e T₄ = 300 ^oC, P₄ = 40 bar.

Disegniamo sul piano pv la trasformazione operata dalla caldaia.

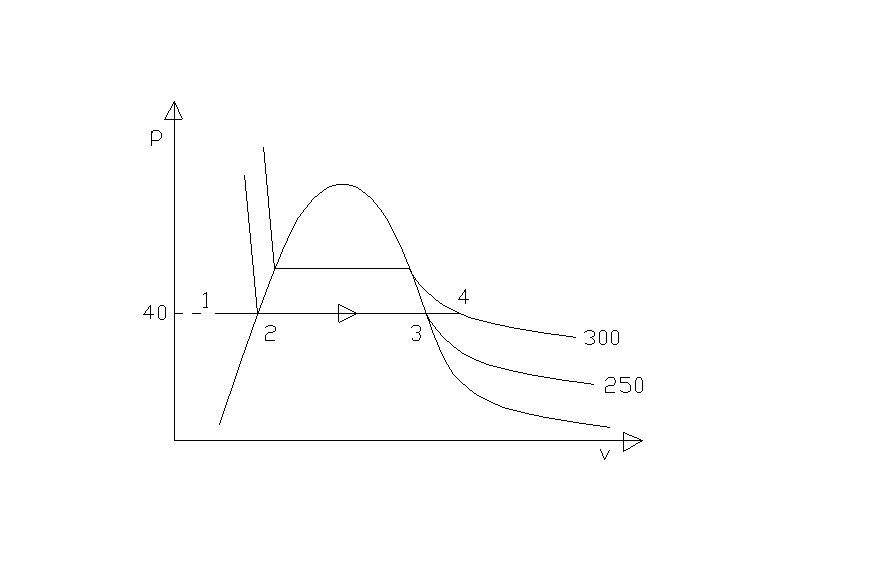
Fig.2: - rappresentazione della trasformazione sul diagramma pv

• 1è 2 : L’acqua, rimanendo allo stato liquido, viene scaldata dalla temperatura iniziale T₁ fino al punto di ebollizione. Dalle tabelle si ha che la temperatura di ebollizione, ovvero la temperatura di saturazione corrispondente ad una pressione P₁ = P₄ = 40 bar è T_s = T₂ = 250 ^oC .
• 2è 3: Processo di vaporizzazione: viene fornito calore per portare l’acqua dallo stato liquido allo stato di vapore saturo secco. E’ una trasformazione a temperatura costante quindi T₂ = T₃.

• 3è 4: Viene fornita una ulteriore quantità di calore per portare il vapore dalla temperatura di 250 ^o C a T₄. Dato che T₄ è maggiore della temperatura di saturazione corrispondente alla pressione di 40 bar, la trasformazione avviene al di fuori della curva limite e si ottiene in uscita del vapore surriscaldato.

Indichiamo con q la quantità di calore da determinare: dato che M = 1kg è una quantità di calore per unità di massa.

Applichiamo al sistema il I principio della termodinamica in forma entalpica.

Poiché la trasformazione avviene a pressione costante si ha che e quindi, integrando, il valore richiesto risulta essere uguale al salto di entalpia.

(3)

(4)

Il calore specifico è una grandezza tabulata: nel nostro caso c_L = 4,187.

(5)

Nel caso in esame r =1713.

(6)

Tabella del calore specifico medio del vapore d’acqua surriscaldato misurato dalla temperatura di saturazione alla temperatura assegnata

In generale nel campo dei valori surriscaldati la variazione di entalpia non dipende solo dalla temperatura ma anche dalla pressione: quello in esame è un caso particolare in quanto avviene una trasformazione a pressione costante.

Sostituendo (4),(5) e (6) in (3) si ottiene la quantità di calore cercata

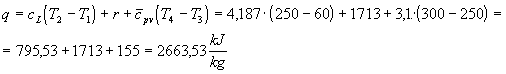
Osservazione: Nel campo del vapore d’acqua, relativamente alle trasformazioni dello stesso tipo di quella operata dalla caldaia, si verifica sempre una sorta di fenomeno di "compensazione". Supponendo di aumentare la pressione e la temperatura si ha che diminuisce il calore latente di vaporizzazione, ma crescono in proporzione i termini di calore relativi alle trasformazioni nel campo del liquido e del vapore surriscaldato. Quindi la quantità di calore necessaria a vaporizzare una massa

di 1kg di acqua è sempre dell’ordine dei 2500-2700 .

Si consideri una pentola a pressione, ovvero un recipiente rigido indeformabile dotato di una valvola. La si riempia in parte di acqua e la si metta sul fuoco con la valvola aperta. Fornendo calore al sistema la temperatura dell’acqua cresce fino a raggiungere quella di ebollizione. Supponendo di essere alla pressione P₁ = 1 bar, la temperatura di ebollizione risulta essere T₁ = 100 ^oC. Se si continua a fornire calore comincia a prodursi del vapore: questo spinge fuori, attraverso la valvola, l’aria presente nella pentola . Quando tutta l’aria è stata espulsa, la valvola viene chiusa. In questa condizione la pentola contiene del vapore saturo ovvero acqua liquida in equilibrio con il suo vapore. Si supponga che vi siano 10kg di acqua liquida e 1kg di vapore. Determinare l’ulteriore quantità di calore che è necessario fornire la sistema per portare la sua pressione dal valore iniziale P₁ al valore P₂ = 5 bar e il titolo x₂ della nuova situazione di equilibrio.

Fig.1-schematizzazione della pentola a pressione

La trasformazione effettuata dalla pentola consiste in un aumento di pressione a volume costante: il volume non può aumentare in quanto si è supposto il recipiente rigido e indeformabile.

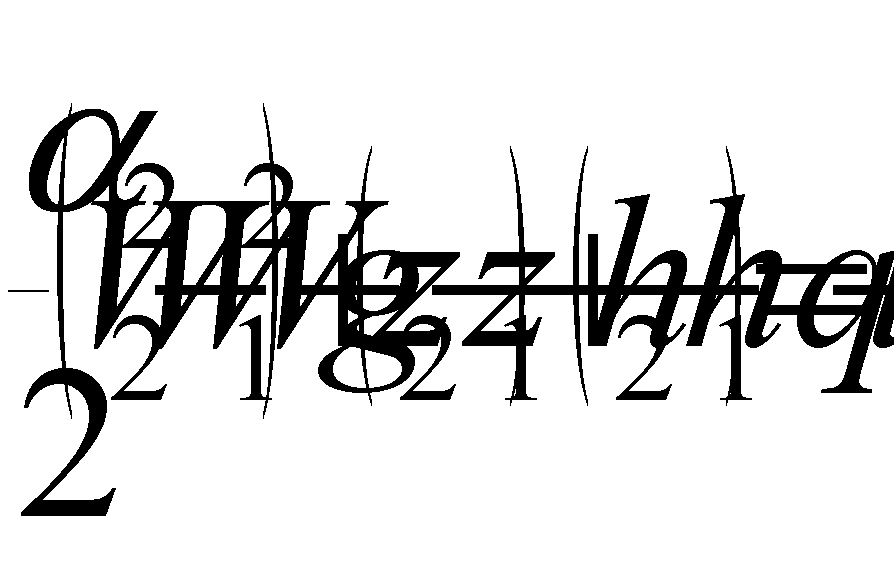
Fig.2- rappresentazione della trasformazione sul diagramma pv

Indichiamo con Q il calore cercato. Applichiamo al sistema chiuso "pentola" il I principio della termodinamica.

(1)

Dato che la trasformazione non comporta un cambiamento di volume non vi è nessuno scambio di lavoro con l’esterno quindi e il calore Q risulta essere uguale alla variazione di energia interna

(2)

Per calcolare le energie interne specifiche del vapore saturo alle pressioni P₁ e P₂ prendiamo come riferimento gli stati liquidi corrispondenti.

(3)

(4)

con e energie specifiche differenziali.

Il titolo x₁ lo si può calcolare facilmente

(5)

Per calcolare il titolo x₂ è sufficiente considerare che la trasformazione tra il punto 1 e il punto 2 avviene a volume costante quindi

(6)

ovvero

(7)

in cui sono stati usati i volumi specifici degli stati liquidi e i volumi specifici differenziali.

Risolvendo rispetto a x₂ si ha

(8)

(9)

Possiamo ora sostituire i valori trovati nelle (3) e (4)

(10)

(11)

sostituendo (10) e (11) in (2)

I valori numerici sono stati ricavati facendo riferimento alla seguente tabella del vapore d’acqua.

Si consideri un tubo dentro al quale sta scorrendo del vapore saturo. Tramite un manometro si calcola che la pressione dentro al tubo è P = 40 bar.

Fig.1

Determinare il titolo x₁ del vapore.

E’ possibile determinare sperimentalmente il titolo di un vapore saturo che scorre entro un condotto operando secondo lo schema seguente. Sulla parete laterale del condotto viene praticato un foro, di opportune dimensioni, al quale viene collegata una conduttura comunicante con l’esterno. Lungo questa conduttura viene inserita una valvola con l’apertura regolabile a piacere. A valle della valvola è predisposto un punto di misura per la temperatura del vapore fuoriuscente: allo scopo è sufficiente usare un termometro a mercurio. La temperatura letta nel caso in esame è T₂ = 115 ^oC .

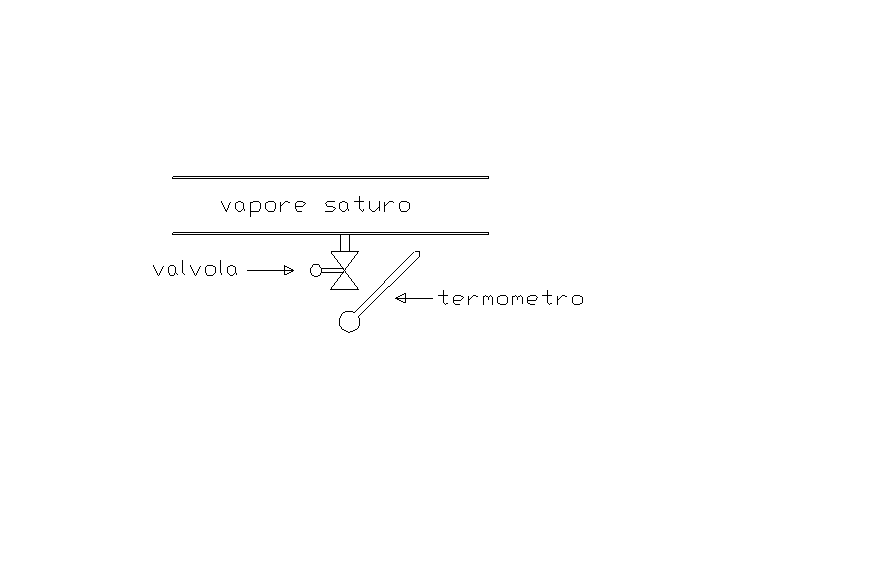
Fig.2

Il condotto entro cui scorre il vapore e la valvola costituiscono un sistema aperto: per determinare il titolo è sufficiente studiare questo sistema supponendo che la fuoriuscita del vapore attraverso la valvola avvenga sotto opportune condizioni.

Nell’ipotesi di poter trascurare i contributi di energia cinetica ed energia potenziale l’equazione di bilancio dell’energia per un sistema aperto può essere scritta come

(1)

Supponiamo ora che il vapore venga fatto fuoriuscire dalla valvola tramite un processo di laminazione. Supponiamo cioè che l’apertura della valvola sia tale (in generale molto piccola) per cui il vapore esca senza scambiare calore con l’esterno, sia già in equilibrio di pressione con l’ambiente ovvero sia alla pressione atmosferica, e abbia una velocità talmente bassa da poter trascurare qualsiasi termine di energia cinetica. Questa è una trasformazione adiabatica a lavoro nullo: non vi è nessuno scambio di lavoro perché il fatto che il vapore esca in equilibrio di pressione con l’ambiente fa si che non vi sia nessuna espansione . La (1) diventa quindi

(2)

Rappresentiamo la trasformazione sul diagramma pv. Il percorso tra 1 e 2 è stato tratteggiato in quanto la trasformazione è irreversibile e gli unici stati di equilibrio, e quindi effettivamente rappresentabili, sono quello iniziale e quello finale.

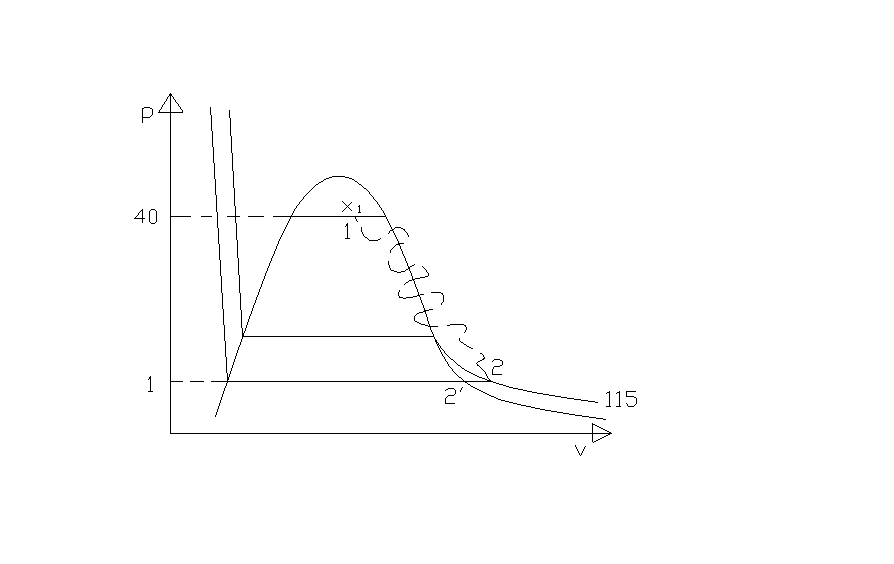
Fig.3

Considerando i valori specifici delle entalpie si ha

(3)

dove r₁ è il calore latente di vaporizzazione alla pressione di 40 bar e h_L1 è l’entalpia specifica dello stato liquido corrispondente.

E

(4)

dove h₂ è l’entalpia specifica del vapore surriscaldato, c_pv è il calore specifico medio a pressione costante del vapore e 2’ è il punto che si trova sulla curva limite superiore in corrispondenza di una pressione di 1 bar quindi T_2’ = 100 ^oC.

Uguagliando (3) e (4), risolvendo rispetto ad x₁ e sostituendo i valori numerici che si possono ricavare dalle tabelle degli esercizi precedenti si ottiene il risultato voluto

(5)

In allegato alla tesina ho voluto aggiungere un formulario generale di FISICA TECNICA , per una consultazione rapida ed essenziale da parte di quei prossimi alunni ,che come me, dovranno affrontare la materia.

1ml=1cm³; 1l=1dm³=10³ml;1m³=10³l

760toor=760mmHg=1atm=10⁵Pa

1watt=1joule/1sec

1bar=10⁵Pa=1atm=7,57*10²toor

joule=Newton*m; Newton=(Kg*m)/s²

Pa=N/m²

Bar=m³/Kg

Interpolazione Y=((XV-XS)/(XI-XS))*(YI-YS)+YS

Tempo di rilassamento µ V^1/3/c dove c=3E⁸m/s e V è il volume

I Principio Termodinamica: U+1/2 m v²+mgz=Q-L considerando trascurabili i termini dovuti all’energia cinetica e potenziale si ha D U=Q-L il lavoro Lrev=ò p dv

Come bilancio: q.entrante + q.prodotta = q.uscente + q.distrutta + D q

Legge 0 : due sistemi in equilibrio termico con un terzo sono in equilibrio termico fra di loro.

Entalpia: H=U+PV a volte si usa per il calcolo di u=h-pv ma dalle tabelle si deve fare attenzione alle unità di misura perché 1atm=1.013e⁵ Pa, se tutto si prende dalle tabelle dovendo convertire in Kj si dovrebbe moltiplicare per 10^-3 si moltiplica il pv per 10²

Entropia si postula la sua esistenza come una grandezza estensiva, monotonicamente crescente cioè (¶ S/¶ U)>0 e nulla solo se la temperatura è nulla (¶ U/¶ S)_V

Reversibilità per un sistema isolato D S=0 reversibile (ideale) D S>0 irreversibile (reale) D S<0 impossibile

I eq. di Gibbs dS=dU/T+(p/T)dV Þ (isocora) dS=dU/T Þ dS=c_vdT/T

II eq. di Gibbs dS= dH/T-(V/T) dp Þ (isobara) dS=dh/T Þ dS=c_pdT/T

Bilancio di entropia Qe/Tsete+P=D S+Qu/Tsetu dove P è la produzione entropica

Definizione di calore: è quella iterazione energetica che porta associato un flusso di entropia

Rendimento Carnout h =1-Tb/Ta Reale h =1-Qb/Qa di II legge h _II=h /h _MC

COP_F=Qb/L=1/((Ta/Tb)+(PTa/Qb)-1) Reversible COP_F,REV=Tb/(Ta-Tb)

Pompa COP_P,REV=Ta/(Ta-Tb)

II specie COP_F,II= COP_F/ COP_F,REV

Gas Ideale D u=CvD T; D h=CpD T specifiche quelle estensive devo moltiplicare per la massa; la T a cui prendo Cv e Cp è quella media T=(T1+T2)/2

Regola fasi o di Gibbs il numero delle grandezze indipendenti sono V=3-F dove F sono il numero delle fasi

D s=Cv*ln(T2/T1)+R*ln(V2/V1); D s=Cp*ln(T2/T1)-R*ln(P2/P1) i Cv e Cp li prendo a T=(T2-T1)/ln(T2/T1)

T-P permette di vedere la fase

Titolo X=m_VS/(m_l+m_VS) dove le m sono le masse del liquido e del vapore saturo rappresenta la quantità di vapore rispetto a quella totale. Si hanno le seguenti v=v_l+x(v_VS-v_l); h=h_l+x(h_VS-h_l); u=u_l+x(u_VS-u_l); s=s_l+x(s_VS-s_l);

Calori specifici c_v=(¶ u/¶ T)_v; c_p=(¶ h/¶ P)_p; c_p(T)=a+bT+cT²+dT³ ; c_v(T)=(a-R)+bT+cT²+dT³

Relazione di Mayer ; c_p- c_v=R 0

Condizioni gas ideali: D u=CvD T; D h=CpD T si considerano pressione e temperatura ridotta e devono sussistere le seguenti p =P/Pc<0,15 e J =T/Tc>1 in queste ipotesi vale PV=nRT oppure PV=RT dove P=KPa, V=m³;T=K;m=Kg R dipende dal gas pag 271con R=R/m e R=8,314 Kjoule/KmoliK.Ñ U=ò _T1^T2 c_v(t)dt=c_v(T2-T1); .Ñ H=ò _T1^T2c_p(t)dt=c_p(T₂-T₁); D s=Cv ln (T₂/T₁)+R ln(V₂/V₁) oppure D s=Cp ln (T₂/T₁)-R ln(P₂/P₁)

Trasformazione adiabatica endoreversibile (valida per le espansioni in turbine) se i calori specifici sono cost T2/T1=(P2/P1)e e T2/T1=(V1/V2)^k-1 oppure P2/P1=(V1/V2)^K scrivibili nelle forme T/Pe =cost; T*V^k-1=cost; P*V^k=cost. con e =k-1/k=R/cp=Cp/Cv

Se i calori specifici non sono costanti:(s(T2)/R)-(S(T1)/R)=ln(P2/P1)Þ P2/P1=(exp(s(T2)/R)/exp(S(T1)/R))

INDIVIDUAZIONE STATO: Uso o il diagramma P-T o le tabelle. Rispettivamente ho entrando con la pressione o con la temperatura

b l(a ^*)=b ^* Þ liquido saturo curva limite inferiore uso il titolo x=0

a ^* b l(a ^*)<b ^* <b s(a ^*) Þ bifase "Per la risoluzione ricavo il titolo dalle tabelle e poi le proprietà"

b vs(a ^*)<b ^*Þ surriscaldato

LIQUIDO INCOMPRIMIBILE vH₂O=1*e^-3 Kg/m³ e c=4.19 Kj/KgK

Energia interna:D U=c D T se interessa la variazione oppure u(T)=uo+c(T-To)

Entropia: D S₁₂=c ln(T₂/T₁) se interessa la variazione oppure s(T)=s_o+c ln(T/To)

Entalpia: D h=v D P si considera una isoterma oppure h=ho+c (T-To)

CONDIZIONI DI SATURAZIONE: uso le tabelle con il titolo

AL DI SOPRA DELLA CURVA A CAMPANA: vapori surriscaldati uso i diagrammi

Condizioni acqua:c=4,19 kJ/KgK; v=1e^-3 Kg/m³

Densita: inverso volume specifico; r =1/portata; m=r wA=V/v (portata (wA= V su volume specifico)

Continuità della massa: m_i=m_u+¶ m_VC/¶ J

I Principio: m_i(h+gz+w²/2)_i+Q_1i+L_e2= m_u(h+gz+w²/2)_u+Q_2u+L_e1+¶ E_VC/¶ J

II Principio: m_iS_i+Q/Ta+P= m_uS_u +¶ S_VC/¶ J

Equazione energia meccanica: l=-[ò ₁²vdp+gD z+D w²/2+r]

1) 1 in, 1 out

2) 1-D

3) ¶ /¶ J =0

4) liquido ideale v=cost

5) condotta a sezione circolare f =cost

Se Ai=Au Þ Wi=Wu; v(Pu-Pi)=g(Zi-Zu)-r; Pu=Pi+r g(Zi-Zu)-r r

6’)condotta rettilinea Þ Zi=Zu Þ Pu=Pi-r r

6’’)condotta inclinataÞ Pu= Pi+r g(Zi-Zu)-r r

Perdite r: concentrate=x w²/2; distribuite=f*L/D*w²/2; quelle concentrate si riconducono a quelle distribuite con L_eq=Dx /f

TURBINA A VAPORE: macchina motrice dinamica con fluido di lavoro vapore surriscaldato o vapore saturo o entrambi. 1 in, 1out; 1-D; ¶ /¶ J =0; Q<<L; gD z» 0 e D w²/2» 0

m_i=m_u=m

m_ih_i= muh_u+L Þ L= m(h_i-h_u)

m_iS_i+P= m_uS_u Þ P=m(S_u-S_i)

Caso ideale P=0 Þ S_u=S_i isoentropica (adiab+ int. rev) nella realtà P>0 Þ S_u>S_i

L_rev=( h_i-h_us); L_reale=(h_i-h_u) Rendimento h _is,TV=l/lrev= h_i-h_u/ h_i-h_us

Individuo la condizione di ingresso e nota la Pu ricavo nel grafico H-S la trasformazione, individuo cosi il lavoro reversibile.

TURBINA A GAS: macchina motrice (da lavoro) dinamica. Le ipotesi sono (1in, 1out), (1-D), (¶ /¶ J =0), (ingegneristicamente adiab Q=0), (D g z=0, D w ²/2=0), (gas ideale cp=cv=cost). Si possono usare indifferentemente i piani T-S e H-S sono gli stessi a meno di una costante.

mh₁=L+mh_2Þ L=m(h₁-h₂)= m cp(T₁-T₂) per i gas ideali D h=cpD T

h _is,TG=l/lid= T₁-T₂/ T₁-T_2s= h₁-h₂/ h₁-h_2s

Nelle ipotesi di idealità politropica pv^k=cost; k=cp/cv; e =(k-1)/k; T/pe =cost; lrev=RT*e *[1-(p2/p1)e ]; essendo h solo f(T) allora lrev= h₁-h_2s=cp*(T1-T2s) e T2s=T1*(P2/P1)e

m_i=m_u=m

mh₁= mh₂ Þ h₁=h₂

mS₁+Sgen= mS₂ Þ Sgen=m(S₂-S₁)

liquidoÞ v=cost Þ D S=cln(T₂/T₁)Þ Tu>Ti (se nel liquido restringo la sezione diminuisce P ed aumenta T)

aeriformeÞ u=u(T) e h=h(T) essendo (h₁=h₂)Þ T₂=T₁

Se non posso usare PV=nRT uso l’indice di Joule Tomson m =¶ T/¶ p| _h

Grafico P-T ottenuto unendo i punti in cui si annulla la derivata

m <0 diminuisce p Þ aumenta T se m >0 diminuisce pÞ aumenta T

m₁=m₂=m

m h₁+L= m h_{2 Þ} L= m( h₂-h₁)= m D h

mS₁+P= mS₂ Þ P=m(S₂-S₁)= m D S

fluido incomprimibile v=cost Þ L= m (cD T+vD P)

P=m c ln(T₂/T₁) se (P>0Þ T₂>T₁; P=0 Þ T₂=T₁=costÞ L= Lrev= mD P

Adiab+int.rev Þ D S=0 uso il piano P-v per il lavoro lrev=D h

Dal piano T-S traccio le due isobare S_B-S_A=c ln(T_B /T_A) Þ S_B=S_A se T_B =T_A

Uso il piano h-.s h _IS,P=lrev/l=(h_2S-h₁)/(h₂-h₁)=v(p2-p1)/(c(T₂ -T₁)+v(p2-p1))

Le ipotesi sono (1in, 1out), (1-D), (¶ /¶ J =0), (ingegneristicamente adiab Q=0), (D g z=0, D w ²/2=0), (gas ideale cp=cv=cost).

m₁=m₂=m

m h₁+L= m h_{2 Þ} L= m( h₂-h₁)= m D h essendo gas ideale Þ L= m cp(T₂-T₁)

mS₁+P= mS₂ Þ P=m(S₂-S₁)= m D S essendo gas ideale Þ P=m[cp ln(T₂/T₁)-R ln((P₂/P₁)]

Se è int. Rev. + adiabÞ P=0Þ L= L_rev= m cp(T_2S-T₁) e Þ 0=m[cp ln(T_2S/T₁)-R ln((P₂/P₁)] con P₂=P_2S

Nella realtà P>0Þ D S>0

h _IS,P=lrev/l=(h_2S-h₁)/(h₂-h₁)= essendo gas ideale=(T_2S-T₁)/( T₂-T₁)

La int.Rev. + adiab è una politropica di esponente k P₂V₁^k= P₂V_2S^k equivale a T_2S/ P_2e = T₁/ P_{1e Þ} T_2S= T₁(P₂/ P₁) ^e =T_{1b e} con b = P₂/ P₁ rapporto di compressione allora lrev=cp(T_2S-T₁)=cpT₁(b e -1)

Nelle stesse ipotesi risulta anche lrev=-R T₁(K/(K-1))[b e -1]

m₁+m₂=m₃; m₁h₁+m₂h₂= m₃h₃; m₁s₁+m₂s₂+Sgen= m₃s₃

Caldaia: mh₁+Q= mh₂; ms₁+Q/Tset+Sgen= ms₂

Fluidi a ¹ temp. Separati:m_ch_ic+m_fh_if=m_ch_uc+m_fh_uf; m_cs_ic+m_fs_if+Sgen=m_cs_uc+m_fs_uf

Efficienza=e =Qscambiato/Qmax=Cc(Tic-Tuc)/Cmin(Tic-Tif)=Cf(Tuf-Tif)/Cmin(Tic-Tif) Cmin=m c dove c è quello più piccolo tra i due

Se usiamo due SC: m_ch_ic= m_ch_uc+÷ Q÷ ; m_fh_if+÷ Q÷ = m_fh_uf

Gas id. e cp,cv costÞ D h=cpD T

1Þ x=0 tabelle; 2Þ h_2s=h1+vÑ P con p in kPa;3=molier;4=tabella;5=molier

Q_a+Lp=Q_b+L_t; Q_a/Ta+Sgen=Qb/Tb

h =(lt-lp)/qa=((h₃-h₄)-(h₂-h₁))/(h₃-h₂)=1-(qb/qa)=1-((h₄-h₁)/(h₃-h₂))

rendimento con rigenerazione: h =l_netto/qa=(l_TA+l_TB-l_P)/(q₂₃+q_4’3’)

Portata massica unitaria PMU=m/(Lt-Lp)=l/(lt-lp)=l/(((h₃-h₄)-(h₂-h₁))

Pompa isoentropica 1-2

m h₁+Lp= m h_{2 Þ} Lp= m( h₂-h₁)= m D h; ms₁+Sgen= mS₂ Þ Sgen=m(S₂-S₁)= m D S

Caldaia isobara 2-3: mh₂+Qa= mh₃; ms₂+Qa/Ta+Sgen= ms₃

Turbina isoentropica 3-4

Condensatore isobara 4-1: mh₄=Qb+mh₁; ms₄+Sgen= ms₁+Qb/Tb

Joule:con rendimenti unitari(ideale),gas ideale cp,cu=cost:T₂/T₁=T₃/T₄=b e ; b =Psup/Pinf=P2/P1=P3/P4; e =(K-1)/K=R/cp; t =Tmax/Tmin=T₃/T₁ ;.

h =(Lt-Lc)/Qa=m[(h₃-h₄)-(h₂-h₁)]/ m(h₃-h₂)=cp[(T₃-T₄)-(T₂-T₁)]/ cp(T₃-T₂)=1-(Qa/Qb)=1-(( T₄-T₁)/( T₃-T₂))

Reale con irreversibilità :T₂=T₁+((T_2s-T₁)/h _c); T₄=T₃- h _t(T₃-T_4s); h = 1- ((mcp(T₄-T₁))/(mcp(T₃-T₂)))= 1-(( T₃- h _t(T₃-T_4s)-T₁)/(T₃-T₁-((T_2s-T₁)/h _c)));

Lnetta=mcp[h _t(T₃-T_4s)- T_2s-T₁)/h _c] ;

Frigorifero:ideale COP_f,rev= Q_EV/(L_C-L_T)

Reale fatto con valvola: Q_B+L_C=Q_A; Q_B/T_B+S_gen=Q_A/T_A;per le altre relazioni si fanno i bilanci sui componenti;

COP_f= Q_B/L_C=(h₁-h₄)/(h₂-h₁)==((h₁-h₄)/(h_2s-h₁))h _C; PMU=m/Q_B=l/q_B=l/ h₁-h₄; (por vol unit)PVU=V₁/ Q_B=v1/( h₁-h₄)

POMPA:COPp,rev=Ta/(Ta-Tb); COPp=Qa/Lc==(h₂-h₃)/(h₂-h₁)==((h₂-h₃)/(h_2s-h₁))h _C;

PMU=m/Qa=1/qa=1/ h₂-h₃; PVU=V₁/Qa=v₁/ h₂-h₃

CONDUZIONE legge di Fourier q=-K D T: si ha quando i due corpi sono a contatto e non vi sono moti macroscopici

Analogia con circuiti elettrici q=D T/((L/(kA)); Ri=Li/(KiAi); Re=1/(heAi)

Eq. della conduzione: Ñ ²T+u’’’/K=1/a(¶ T/¶ q ) dove a=k/r c diffusività termica

Eq Laplace Ñ ²T=0 ipotesi u’’’=0 e ¶ /¶ q =0

Eq. Poisson Ñ ²T=-u’’’/K ipotesi u’’’¹ >0 e ¶ /¶ q =0

Eq. Fourier Ñ ²T=1/a(¶ T/¶ q ) ipotesi u’’’=0 e ¶ /¶ q ¹ 0

Nel caso di monodimensionalità Ñ ²T/¶ x²+u’’’/K=1/a(¶ T/¶ q ) con 3 condizioni ai limiti 2 geometriche per il laplaciano e una temporale per ¶ T/¶ q

Simmetria piana senz. gener: T(x)=(T₂-T₁/L)*X+T₁ e Q=(AK/L)*( T₁-T₂) analogia corrente Q=D T/R con R=L/AK (vedere eventuali inclinazioni + k è grande + è inclinata)

Simmetria cilind. senz. gener: T(r)= T₁- (((T₁-T₂)/(ln(r₂/r₁))*ln(r/r₁) e Q=2p lk((T₁-T₂)/ln(r₂/r₁));R= ln(r₂/r₁)/2p KL; Rest=1/(2p r₂Lhe)

Simmetria sferica senz. Gerner: T(r)=T₁-(((T₁-T₂)/(1/r₁-1/r₂))* (1/r₁-1/r)) e Q=(T₁-T₂)/((4p k)^-1((1/r₁-1/r₂))

Lastra piana con generazione: (1-D; u’’’¹ >0; ¶ T/¶ q =0) d²T/dx²=-u’’’/K diventa T(x)= (-u’’’/2K)*x²+(-u’’’/2K)*L²+(-u’’’*L/h)+T¥ essendo la piastra simmetrica rispetto all’asse risulta anche T(L)= u’’’*L/h)+T¥ ; D Tmax=u’’’*L²/2K; D Te= u’’’*L/h

Cilindro con generazione: (L>>r_eÞ 1-D; u’’’>0; ¶ T/¶ q =0): T(r)=(-u’’’/4k)*r²+(u’’’/4k)*re²+ (u’’’/2h)re+ T¥ e Q(r)=4p u’’’ r ³/3

Raggio critico di isolamento:Q=(Ti-T¥ )/Riso+Rest; Risol= ln(r₂/r₁)/2p KL; Rest=1/(2p r₂Lhe)

Bi=hL/k=hA/(KA/L)=cond. Super/cond.condut=res cond/res. Super Bi piccoloÞ res. Cond trascurabileÞ T=T(q )

Fo=aq /L²=Kq /(r cpL²)=((K/L)L²)/(r cpL³/q )=pot. Cond. Att. L nel Volume L³/pot. Accumulata + Fo è grande + vi è flusso di Q e non vi è accumulo

E=potere emissivo; J=radiosità (emessa+riflessa); G=irradiazione (quella che incide);

a =coeff. di assorbimento a _med.=å a l Gl /å Gl ;r =coeff. di riflessione;t =coeff. di trasmissione e a +r +t =1 G=a G+r G+t G

Legge di Plunk: Enl (T)=C1/(l ⁵(e^{C2/l T}-1) l’energia totale emessa da un corpo nero (emettitore perfetto) è pari a En=ò _0¥ Enl dl =s T⁴ con s costante di stefan-boltzman Nel vuoto C1=3,74e⁸[m m⁴K/m²];C2=1,44*10^4m mK; l [m m]; En [W/m²]

Legge di Wien l _MAXT=C₃ con C₃=2898 m m K

Velocità di propagazione c=1/Ö m l

Emittenza e =El /Enl Þ El =e *Enl Þ E=e s Ts⁴

Irraggiamento per corpo nero: En(T)=n^2s T⁴ dove n=indice rif» 1 per aria e gas e s =5,67e^-8 [W/m²K⁴]Fattore di configurazione geometrica:F_i-j=Jche lascia Ai ed incide su Aj/ J totale che lascia Ai; A_iF_i-j=A_jF_j-i; F_i-j+F_j-i=1; F_1-2 =F_1-3+F_1-4 ho diviso 2 in 3e4;

Piastre nere:q_1-2=En1-En2=s (T₁⁴-T₂⁴)

Piastre grige:e =cost per una certa T in un intervallo di l  ; per esso e =e l ; a =a l ; a =e ;per due piastre risultano vere le seguenti:J₁=E₁+(1-e ₁)G₁; J₂=E₂+(1-e ₂)G₂;essendo parallele risulta J₁=G₂ e J₂=G₁ da queste si ha J₁=( E₁+(1-e ₁)E₂)/(e ₁+e ₂-e ₁*e ₂) e G₁=( E₂+(1-e ₂)E₁)/(e ₁+e ₂-e ₁*e ₂) da q_i=J_i-G_i si ha q_1-2=(e ₂E₁-e ₁E₂)/(e ₁+e ₂-e ₁*e ₂) da E(Ts,sup)=e (Ts,sup)s T⁴ si ha: q_1-2=(e _{2e 1s} T₁⁴-e _{2e 1s} T₂⁴)/( e ₁+e ₂-e ₁*e ₂) cioè q_1-2=s (T₁⁴-T₂⁴)/(1/e ₁+1/e ₂-1)

Schermo radiativo:la q diventa metà con 1, 1/3 con 2; 1/4 con 3 si dimostra facendo il circuito totale con le resistenze

Analogia elettrica;Re =(1-e )/(e A); Rvuoto=1/F_1-2A1; Q=s (T₁⁴-T₂⁴)/Req

CONVETTIVO Q=hc A(Ts-T¥ )

avviene in due modi forzato per ventilazione e libero causato dalla forza di Archimede.

Numero di Reynolds Re=(r u¥ L)m = u¥ L/n

Numero di Prandtl Pr=m c/k=n /a con n =m /r viscosità cinematica

Numero di Eckert Ec= u¥ ²/cD T

Numero di Nusselt Nu= (hc L)/Kf

Numero di Grashof GR=(g b D T L³)/n ²=r ² g b D T L³/ m ²

Numero di rayleigh RA=GR*PR=Fg/Fv= (g b D T L³)/n a=r g b D T L³/ m a

Per piastra Recrit=3,5*10⁵ se Rex>RecritÞ regime turbolento dove Rex= u¥ x/n

Per condotto: Diametro eq=De=4A/Perimetro bagnato; Re=(uDe)/n ; velocita media u=V/A

Lunghezza d’imbocco per flusso laminare è Li=0,03 De*Re

Lastra piana: devo calcolare Q=hc A(Ts-T¥ ); hc lo ricavo da Nu= (hc L)/Kf; Calcolo Pr e poi considero i vari casi per il calcolo di Nu

Nu=0,064 (Pr)^1/3 (Re)^1/2 per 0,6£ Pr£ 10 L=lunghezza caratteristica=lunghezza nella direzione del flusso

Nu=0,0678 (Pr)^1/3 (Re)^1/2 per Pr® ¥

Nu=1,13 (Pr)^1/2 (Re)^1/2 =1,13 (Pe)^1/2 per Pr® 0

I valori di k, Pr, a, n li prendo a pag 287 ed entro con la Trif=T¥

Sfera Nu=(heDe)/k=2 per Re® 0; Q(Rag.est)=4p re k(Ts-T¥ )=4p re² hc(Ts-T¥ ) xchè k= re hc; L=diametro esterno

Flusso normale a cilindro: Nu=(0,4(Re)^1/2+0,06(Re)^2/3)(Pr)^2/5(m ¥ /m s)^1/4 per 1<Re<10⁵; 0,67<Pr<300; L=diametro esterno

LIBERA Trif=Tfilm=(Ts+T¥ )/2:

Numero di Grashof GR=(g b D T L³)/n ²=r ² g b D T L³/ m ²

Numero di rayleigh RA=GR*PR=Fg/Fv= (g b D T L³)/n a=r g b D T L³/ m a

Grx= (g b D T x³)/n ²

Rax=Grx*Pr per avere un regime turbolento si deve verificare una delle seguenti : Grx>Grcrit o Rax>Racrit solitamente Racrit=10⁹

Piastra verticale: Nu=0,59 (Ra)^1/4 per 10⁴<Ra<10⁹ laminare; Nu=0,13(Ra)^1/3 per 10⁹<Ra<10³ turbolento; L=altezza

Cilindro orizzontale: Nu=0,53 (Ra)^1/4 se 10⁴<Ra<10⁹ laminare; Nu=0,13(Ra)^1/3 per 10⁹<Ra<10¹² turbolento L=diametro esterno

Cilindro verticale: D/L(Gr)^1/4³ 3,5 dove D=diametro e L=Lunghezza e 0,7£ Pr£ 1 uso la piastra verticale con errore del 5%; L=altezza

Piastra orizzontale:super. Sup. Ts>T¥ e super. Inf Ts<T¥ Þ Nu=0,14 (Ra)^1/3 se Ra>2 10⁸ turbol.

Super. Sup. Ts<T¥ e super. Inf. Ts>T¥ Þ Nu=0,58 (Ra)^1/5 se 10⁶<Ra<10¹¹ laminare Lp.rett=media aritm due lati; Lp.circ=diametr; Lpqualsiasi=rapporto area perimetro.

Sfera : Nu=2+0,43 (Ra)^1/4 se 1<Gr<10⁵ laminare L=diam.ester

Per H₂O Nu=2+0,5 (Ra)^1/4 se 3*10⁵<Ra<8*10⁸ laminare