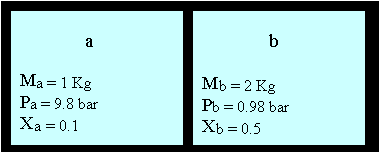
Alessandra Ferretti – Matricola n° 139045 – lezione del 29/11/2001 – ora:16.30-18-30
UNIVERSITA’ DEGLI STUDI DI PARMA
Anno Accademico 2001-2002
Facoltà di Architettura
Corso di FISICA TECNICA
Professore:
ANGELO FARINA
Argomento della lezione:
ESERCIZI SUI VAPORI SATURI
Data e ora della lezione:
29/11/2001 dalle ore 16.30 alle ore 18.30
Trascrittore:
Ferretti Alessandra
ESERCIZIO 1
Abbiamo uno "scatolone" realizzato con un involucro isolante al cui interno è diviso da un setto separatore, che poi cederà. Poiché l’involucro dello scatolone è isolante, possiamo considerare nulla la quantità di calore Q scambiata tra l’interno e l’esterno del recipiente in questione.
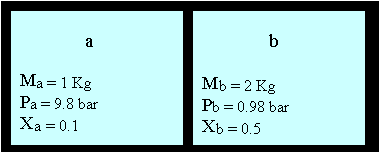
In a, la massa di vapore saturo di acqua è Ma = 1 Kg alla pressione Pa = 9.8 bar = 98 Kpa e titolo Xa = 0.1.
In b, la massa Mb di vapore saturo dell’acqua è pari a 2 Kg, la pressione Pb = 0.98 bar = 9.8 KPa e il titolo Xb = 0.5.
E’ inutile assegnare le temperature Ta e Tb poiché sappiamo che per i vapori saturi ad ogni pressione corrisponde una certa temperatura ricavabile dalle tabelle.
Quindi possiamo dire che le due sotto-parti a e b sono in equilibrio.
Togliendo il setto separatore il sistema non sarà più in equilibrio in quanto avremo a contatto due pressioni diverse e due diverse temperature. Quindi i due gas si mescoleranno, si trasformeranno sino a quando il sistema tornerà ad uno stato di uniformità, si stabilirà un nuovo stato di equilibrio finale detto f.
Osserviamo che
![]()
Vale il principio di conservazione della massa
![]()
La massa finale di vapore saturo di acqua sarà
M
f = Ma + Mb = 3 Kg
V
f = Va + Vbdove Vf è il volume finale ed è così definito:
V
f = Mf × vfcon vf = volume specifico finale
V
a = Ma × vaV
b = Mb × vb ![]()
M
f × vf = Ma × va + Mb × vbcon:
va = vla + xa × vda = 0,001126 + 0,1 × 0,1969 = 0,020816 m3/Kg
vb = vlb + xb × vdb = 0,01043 + 0,5 × 1,724 = 0,863 m3/Kg
vda , vdb = volume specifico differenziale
vla , vlb = volume specifico del liquido
I valori di vda, vdb, vla, vlb sono ricavabili dalle tabelle.
E’ verificato che aumentando la pressione, il volume differenziale aumenta.
vf = volume specifico finale
![]()
vf = Ma × va + Mb × vb = 0,5823 m3/Kg
U
f – ( Ua + Ub) = Q – L = 0Essendo adiabatico possiamo dire che non c’è stato scambio di L e Q!
M
f × Uf = Ma × Ua + Mb × Ub
U
a = Ula + xa × (rf – pf × vda)= 759 + 0,1× (2018 – 980 × 0,1969) = 941 KJ/Kg
U
b = 415 + (2259 – 98 × 1,724) × 0,5 = 1460 KJ/Kg
Quindi:
Uf = ( Ma × Ua + Mb × Ub) / Mf = 1287 KJ/Kg
Uf può anche essere scritto come :
Uf = Ulf + xf × ( rf – pf × vdf ) dove xf e pf sono incognite, ma conoscendo il
valore di Uf si possono determinare i valore di
xf e pf dalle tabelle, andando per tentativi:
1° Tentativo:
p
f = 284 Pax
f = 0,94![]()
Uf = 2425 NON VA BENE!
2° Tentativo:
p
f = 196 Pax
f = 0,65![]()
U
f = 1820 NON VA BENE!
Quindi:
tentativo pf xf Uf
1 284 0,94 2425
2 196 0,65 1820
3 147 0,49 1472
4 118 0,40 1260 pf = 118 Kpa
ho trovato il punto in cui si va a posizionare
la pressione nel sistema!
ESERCIZIO 2
Abbiamo una caldaia:
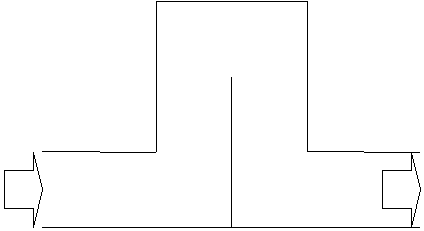
T1 T2
In questo esercizio si vuole determinare il calore necessario per produrre 1 Kg di vapore
Sappiamo che:
T1 = temperatura in ingresso = 60°C
T2 = temperatura in uscita = 300°C
P1 = pressione in ingresso = 40 bar
Quanto calore devo fornire per produrre 1Kg di vapore?
Poiché questo è un sistema aperto:
ENTALPIA FINALE – ENTALPIA INIZIALE = Q – L
Non è applicata alcuna macchina quindi non sono neanche in presenza di un lavoro:
L = 0.
Quindi: ENTALPIA FINALE – ENTALPIA INIZIALE = Q
Q = h4 – h1 = ( h4 – h3 ) + ( h3 – h2 ) + ( h2 – h1 )
h2 – h1 = Cl ( T2 – T1) = 4,187 ( 250 – 60 ) = 795 KJ/Kg
Allo stesso modo avremo che:
h
3 – h2 = 1713 KJ/Kgh4 – h3 = ` Cp × (T4 – T3) = 2,1 ( 300 – 250 ) = 105 KJ/Kg
Quindi:
Q = 2614 KJ/Kg
·
Se ho una portata termica di M= 4 Kg/s, quale potenza termica devo fornire?
· ·
Q = M × Q = 10500 KJ/s = 10500 KW
ESERCIZIO 3
Abbiamo un contenitore isolante in cui ci sono 10 Kg di acqua e 1 Kg di vapore.
Sapendo che la pressione iniziale è P1 = 1 bar e quella finale sarà P2 = 5 bar, si vuole determinare X2 e Q.

Per la legge della conservazione delle masse avremo che:
M
l,1 + Mv,1 = Ml,2 + Mv,2
Dove
M
l,1 = massa iniziale del liquidoM
v,1 = massa iniziale del vaporeM
l,2 = massa finale del liquidoM
v,2 = massa finale del vaporePer la conservazione del volume avremo che:
V
v,1 + Vl,1 = Vv,2 + Vl,2Dove
V
v,1 = volume iniziale del vaporeV
l,1 = volume iniziale del liquidoV
v,2 = volume finale del vaporeV
l,2 = volume finale del liquido
Quindi:
Situazione finale = Situazione finale
M
l,1 × Vl,1 + Mv,1 × Vv,1 = Ml,2 × Vl,2 + Mv,2 × Vv,2Dalle tabelle ricaviamo:
V l,1 = 1,0437 dm3/Kg
V v,1 = 1,673 dm3/Kg
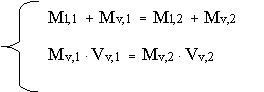
Da cui
M
v,2 = Mv,1 × Vv,1 / Vv,2 = 4,5 KgM
l,2 = Ml,1 + Mv,1 – Mv,2 = ( 10 + 1 – 4,5 ) Kg = 6,5 Kgx
1 = Mv,1 / ( Ml,1 + Mv,1 ) = 0,09x
2 = Mv,2 / ( Ml,2 + Mv,2 ) = 0,41D U = Q
D U = Mtot ( U2 – U1 )
U
2 = Ul,2 + X2 × Ud,2 = Ul,2 + X2 × ( r2 – p2 × vd,2 ) ==
640 + 0,41 × (2107 – 5 × 100 × 0,374) = 1427 KJ/KgAllo stesso modo
U1 = 607 JK/Kg
Quindi
D U = Mtot × ( U2 – U1 ) = 11 × ( 1427 – 607 ) = 9020 KJ
9020 KJ è il calore necessario per far passare la pressione da 1 bar a 5 bar.
ESERCIZIO 4
Siamo in presenza di un tubo al cui interno vi è una pressione pari a 39,7 bar e all’esterno, invece, corrisponde ad 1 bar. A questo tubo è applicato un manometro e un termometro che, attraverso un foro, misura la temperatura all’interno del tubo.
Con questo esercizio si vuole determinare il valore del titolo all’interno della tubazione.
La trasformazione è adiabatica
QUINDI
Non c’è scambio di lavoro!
D H = Q - L
ma
Q = 0 e L = 0
quindi
H2 = H1
conservandosi la massa:
h2 = h1
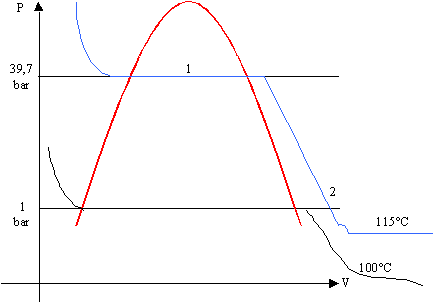
Ricavo T1, temperatura all’interno del tubo, dalle tabelle in base alla pressione:
T1 = 250°C
h
1 = hl,1 + x1× r1h
2 = hl,2 + x2 × r2 + Cp,v × (T2 – T2’) = 4,187× 100 + 2257 + 1,95× (115 – 100) ==
2705 KJ/Kg
Quindi:
h
2 = h1 = 2705 KJ/Kgh
l,1 = 4,187 × 250r
1 = 1715
x1 = [2705 – (4,187 × 250 )] / 1715 = 0,97
ESERCIZIO 5
Abbiamo un recipiente a pareti rigide all’interno del quale vi è una pressione pari a 1kg/cm3 con titolo x1 = 0,644.
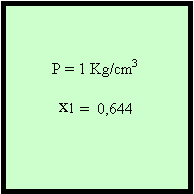
Poiché conosciamo P1, ricaviamo dalle tabelle T1 = 99,1° C
Per la conservazione del volume avremo che :
V1 / M = V2 / M
Quindi
V1 = V2
V1 = Vl,1 + x × Vd,1 = 0,001 + 0,644 × 1,724 = 1,11 m3/Kg
( anche in questo caso i valori sono stati ricavati dalle tabelle)
D U = Q = U2 – U1
U
2 = Ul,2 + x2 × ( r2 – vd,2 × P2 ) = vedi tabelleU
1 = Ul,1 + x1 × ( r1 – vd,1 × P1 ) = vedi tabelle
D U = Q = U2 – U1 = 760 KJ/Kg