VARIE FORME DI ENERGIA

Prima di parlare di energia si rende necessario fare un piccolo richiamo al concetto di lavoro di una

forza.

Il lavoro per definizione è dato dal prodotto di una forza per lo spostamento che questa produce una volta applicata ad un corpo. Nel disegno soprastante possiamo notare come la forza esercitata dal peso agisca su di uno stantuffo, modificandone la posizione e di conseguenza la pressione del gas contenuto nel recipiente e chiuso dallo stantuffo.

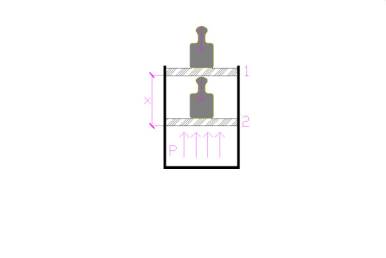Noi sappiamo che una forza è data dal prodotto di una massa per l’accelerazione, in questo caso trattandosi di forza peso e possiamo dire che la massa (1 Kg) del corpo subisca l’accelerazione della forza di gravità terrestre (9.81 m/s2). Il lavoro (L) sarà il prodotto della forza peso (F) per lo spostamento (x) e nella forma abbreviata scriveremo:

L = F * x

Dove F per quanto enunciato in precedenza sarà uguale alla massa (M) moltiplicata per l’accelerazione di gravità (g), scriveremo quindi in forma abbreviata che F = M*g, ma la forza in questo caso si può scrivere in funzione della pressione che lo stantuffo esercita sotto l’azione della forza peso sul gas, avremo quindi la formula sintetica F = M*g = P*S dove P è la pressione e S rappresenta la superficie sulla quale agisce la pressione (l’area di base dello stantuffo).

Riprendendo quindi la definizione di lavoro e la formula sintetica che avevamo ottenuto in precedenza ci accorgiamo che sostituendo alla forza (F) la stessa quantità di Newton ma scritta in funzione di superficie e pressione otteniamo: L = F*x = P*S*x. In questa formula appare il prodotto della superficie (S) per lo spostamento dello stantuffo (x) che il tutto equivale alla variazione di volume : S*x = V2-V1 se ne ricava che il lavoro è uguale alla pressione per la variazione di volume: L = P*(V2-V1)

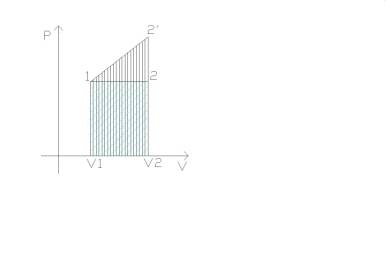
Il grafico sopra riassume il lavoro del sistema prima descritto, rappresentato dall’area sottesa al segmento che rappresenta la variazione di pressione e volume, essendo questo grafico un trapezio la sua area e quindi il lavoro si ricaverà secondo la seguente formula: L = (P2+P1)*(V2-V1)/2. L’area totale è scomponibile in infinitesimi “rettangolini”, la somma di tutte le loro aree darà il lavoro totale, quest’accorgimento è utile nel caso in cui il grafico abbia forma irregolare.

Un altro esempio di macchina che compie lavoro è lo stantuffo rappresentato qua sotto, in un primo la molla che lavora in compressione agisce sul pistone, contrastando la pressione P1, x1 è lo spazio tra fondo del contenitore e pistone. In un secondo momento forniamo calore al sistema e ci accorgeremo che il gas presente nel recipiente si espanderà, raddoppiando la sua pressione e comprimendo al molla, insieme alla pressione aumenta in maniera direttamente proporzionale lo spazio tra fondo del recipiente e pistone.

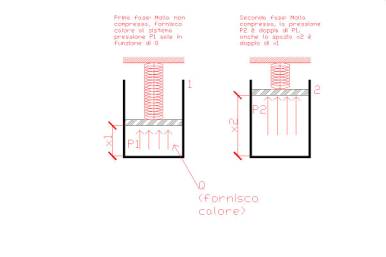
L’esperienza appena descritta è scrivibile analiticamente nel seguente modo: F1 (forza nel primo stadio), F2 (forza nel secondo stadio), k (costante elastica della molla). La forza della molla nel primo stadio è corrispondente alla sua costante elastica moltiplicata per lo spazio x1, cioè F1 = k * x1. La forza della molla nel secondo stadio equivale alla costante elastica per lo spazio x2, è intuibile che il valore della forza in questo momento è doppia rispetto alla precedente valutazione, essendo x1 il doppio di x2. Per quanto riguarda la pressione possiamo affermare che essendo quest’ultima data dal rapporto tra forza e superficie, scriveremo:

x2 = 2 * x1 F2 = k * x2 = k * (2 * x1) si nota che anche analiticamente F2 è doppia di F1 da cui P1 = F1 / S e P2 = F2/S = 2 * F1/S quindi P2 = 2 * P1

L’ENERGIA CINETICA

Questo tipo di energia è legata strettamente a due parametri, la massa e la velocità, per analizzare meglio quest’entità fisica prendiamo in esame il sistema chiuso automobile. L’auto riceve lavoro dal motore, tale lavoro permette al nostro mezzo di spostarsi ad una determinata velocità v, la massa M rimane costante. La formula per ricavare l’energia cinetica è la seguente:

E cin. = 1/2 M * (v*v) e (spec.) = 1/2 * (v*v) (in questa formula non è presente unità di massa perché riguarda l’energia cinetica specifica, cioè è la quantità di energia cinetica tipica di ogni singola unità di massa del sistema preso in esame).

L’ENERGIA POTENZIALE GRAVITAZIONALE

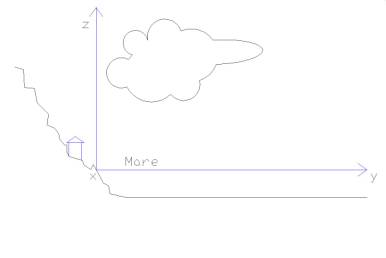
L’energia potenziale gravitazionale è tipica di un corpo che si trova ad una determinata altezza (z) rispetto al livello del mare che considereremo come livello -0-, o per meglio dire il punto di origine delle forze, in questo caso il campo gravitazionale terrestre (g), come per l’energia cinetica è fondamentale la massa del corpo che prendiamo in considerazione.

La quantità di energia potenziale di un corpo di massa (M), sospeso ad un’altezza (z) e sottoposto ad un’accelerazione di gravità (g) sarà data dalla seguente formula:

E pot. = M * g * z e pot. (spec.) = g * z

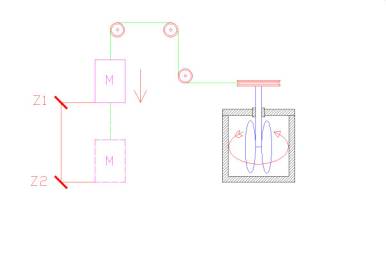
Il seguente esperimento descrive chiaramente il concetto di energia potenziale, dove il peso M si muove dalla posizione z1 alla posizione z2 variando la sua energia potenziale e trasformandola in energia cinetica, la quale tramite un sistema di carrucole sarà trasmessa alla turbina situata nel calorimetro adiabatico, la quale movendosi scalderà l’acqua presente nel calorimetro. L’energia potenziale iniziale si è trasformata in calore o per meglio dire energia termica, immagazzinata nel calorimetro , il quale essendo adiabatico conserverà il calore fino a che non si decida di utilizzare quest’energia termica per produrre lavoro.

L’ENERGIA INTERNA

Rifacendoci alla definizione appena data di energia potenziale come entità fisica legata alla posizione di un corpo, ed una sua eventuale variazione equivale alla produzione di lavoro, ora parallelamente possiamo parlare dell’energia interna, la quale anzi che essere legata alla posizione iniziale di un corpo rispetto ad un dato sistema di riferimento delle forze, è legata al calore iniziale di un corpo. La quantità di calore di un corpo la chiameremo Q, mentre L rappresenterà il lavoro che il corpo compirà utilizzando parte di Q, l’energia interna del corpo verrà indicata con U, detto ciò possiamo procedere alla schematizzazione di quanto detto:

U2 - U1 = ∆U = L pot. L pot. = Q - L

La variazione dell’energia interna (∆U) dal primo stadio U1 al secondo stadio U2 ci fornisce il lavoro potenziale che il corpo o il sistema sono in grado di compiere al cambiamento dell’energia interna.

LA CAPACITA’ TERMICA

La capacità termica di un corpo è la sua capacità di assorbire calore prima di variare di 1° la sua temperatura.

C (H2O) 4187 J/Kg*K

ESERCIZI

1)

P (motore) = 0,5 Cv

τ = 20 min

M H20 (nel calorimetro) = 100 Kg

U2 – U1 = ?

∆T = ?

Per trovare la variazione dell’energia interna e della temperatura procederemo trovando il lavoro con la formula inversa:

1 Cv = 735 W

1 Min = 60 s

L = -P * τ = (0,5 * 735) W * (20 * 60) s = 441600 J

Il lavoro prodotto dal motore equivale alla variazione dell’energia interna del sistema, la variazione d’energia interna è data dal prodotto della massa per la capacità termica per la variazione di temperatura, analiticamente:

U2 - U1 = M * C *∆T in questo caso U2 – U1 = 441600J = M (H2O) * C (H2O) * ∆T

Ricavando la formula inversa troveremo la variazione della temperatura ∆T:

∆T = (U2 - U1) / M (H20) * C(H2O) = 441600 / 100 * 4187 = 1,05 K.

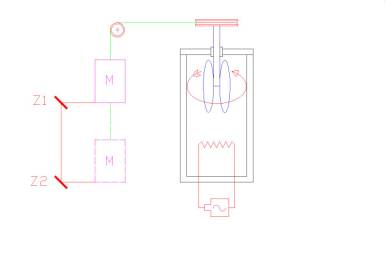
2)

M(H2O) = 100 Kg

R = 0,2 Ω

i = 6 A

τ = 5 min = 300 s

∆z = z1 – z2 = ?

Per trovare la potenza della resistenza dobbiamo utilizzare la legge di Joule, la quale afferma che la potenza equivale al prodotto del valore della resistenza (R) per il quadrato dell’intensità di corrente:

P = R * (i*i) = 0,2 Ω * 36 A = 7,2 W

Per ricavare poi la quantità di calore (Q), dovremo moltiplicare la potenza termica ricavata in precedenza per il tempo:

Q = P * τ = 7,2 W * 300 s = 2160 J

Sapendo che ∆z equivale al lavoro compiuto dal sistema possiamo ricavare la differenza d’altezza con la seguente equazione:

E pot. = M * g * ∆z → 2160 J = 100 Kg * 9,81 m/s2 = 2160 / 100 * 9,81 = 2,20 m