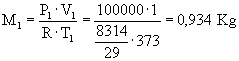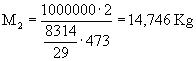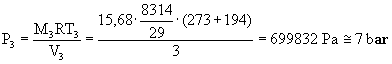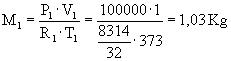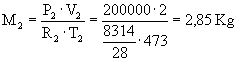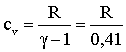Fausto Ugozzoli – matr. 133200 – Lezione del 10/11/00 – ora 10:30-12:30

Esercizi sui gas perfetti.

Esercizio 1.

Vediamo il problema della miscelazione di due gas differenti all’interno di uno scatolone adiabatico (= recipiente isolato dall’esterno mediante pareti coibentate).

Q = 0 (essendo un sistema adiabatico, non avvengono scambi di calore con l’esterno)

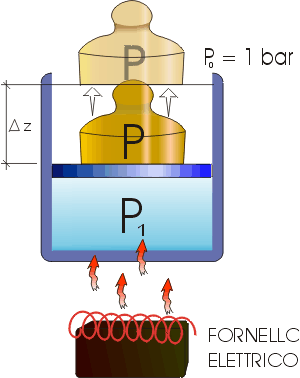
Fig.1 – scatolone adiabatico.

Nota 1: Con 1 e 2 sono indicati i due sistemi. Il setto interno al recipiente, è posto verso sinistra a causa della differenza di pressione tra i due gas.

Nota 2: L'aria è un miscuglio di vari gas, costituito soprattutto da azoto e ossigeno che ne rappresentano circa il 99% del volume. L'aria ha la stessa composizione in regioni e altitudini diverse se non si considerano il vapor d'acqua, il biossido di carbonio, l'ozono, l'ammoniaca, le eventuali polveri e i microbi che per diverse ragioni possono essere presenti in quantità variabili. L'aria priva di essi è detta aria pura e la sua composizione volumetrica è: 20,95% di ossigeno, 78,09% di azoto, 0,94% di argo e gas rari.

Nota 3: Gas perfetto, è un ipotetico gas che segue le leggi di Boyle-Mariotte e di Volta-Gay-Lussac. Un gas si dice gas perfetto se soddisfa all'equazione pv = nRT dove n è il numero delle moli presenti, R è la costante dei gas perfetti pari a 8,314 joule/mole K, T è la temperatura assoluta che è legata alla temperatura t della scala centigrada dalla relazione T = t + 273,16.

Per trasformazioni isoterme l'equazione precedente si riduce alla legge di Boyle-Mariotte che stabilisce la proporzionalità inversa tra pressione e volume per un gas perfetto. L'equazione di stato dei gas perfetti si può ricavare per via teorica, mediante la teoria cinetica dei gas, nelle ipotesi che il volume proprio delle molecole e le loro mutue interazioni siano trascurabili. Queste due condizioni si verificano senz'altro per un gas in uno stato molto lontano dal suo punto di liquefazione. Quindi tutti i gas a temperature sufficientemente elevate e a pressioni sufficientemente piccole si comportano come gas perfetti.

Dati:

V₁=1 m³ V₂=2 m³ T₁=100 °C T₂=200 °C P₁=1 bar P₂=10 bar

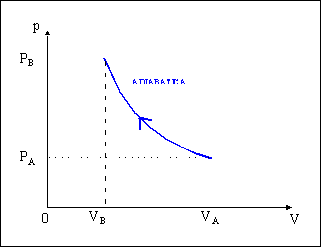
Rimuovendo il setto i gas si mescolano:

Fig.2 – scatolone adiabatico allo stato finale.

Lo stato fisico finale, di equilibrio, si otterrà dopo un periodo di “assestamento”.

Cerchiamo, ora, di ottenere i seguenti dati, calcolati allo stato finale:

Chiaramente V₃= 3m³.

Trovando la temperatura T , la pressione P è facilmente ricavabile dall’equazione di stato dei gas perfetti.

Utilizzando il 1° principio della termodinamica otteniamo: U_FIN- U_IN= Q - L = 0

Nota: le lettere U sono in questo caso maiuscole, in quanto “grandezze estensive” e non “grandezze specifiche”, riferite invece all’unità di massa.

Il lavoro L e la temperatura Q sono nulli in quanto il sistema è termicamente e meccanicamente isolato (quindi l’area sottesa dalla curva nel grafico è nulla) e siccome l’energia interna U (nella forma estensiva) è una grandezza che gode della proprietà additiva, risulta:

U_FIN = U_IN(1)

dove U_IN= U1+U2 e U_FIN = U₃ ; sostituendo nella (1):

M₃c_Vt₃= M₁c_Vt₁+ M₂c_Vt₂(2)

divido per c_v(“media ponderata” o pesata)

Cerchiamo le M: utilizzo PV = MRT (forma “estensiva”) (3)

Nota: siccome la massa molare dell’aria è m_ARIA= 29 Kg/Kmol e che nR₀=MR, segue che R=R₀/m=8314/29 [J/Kmol K].

M₃ = 15,68 Kg

P₃V₃ = M₃RT₃

Nota 1: 100000 Pa = 1 bar

Nota 2: Nelle equazioni di stato la temperatura T è espressa in K (vedi P₃), mentre, ad esempio, quando abbiamo calcolato t_3,è stata espressa in °C.

Esercizio 2:

Fig.3 – scatolone adiabatico.

Dati:

m_O2=32 Kg/Kmol m_N2=28 Kg/Kmol V₁=1m³V₂=2m³

P₁=1 bar P₂=2 bar T₁=100°C T₂=200°C

P3=? T3=? Composizione miscuglio=?

g = 1,41

Nota: Combinando ossigeno e azoto si ottiene “NITROX” (che assume denominazioni differenti a seconda della percentuale di ossigeno presente: al 21%: “aria”; <21%: “nitrox impoverita”; >21%(30-40%): “nitrox”).

M₃=M1+M2=3,88 Kg

Nota: in caso d’incendio, l’ossigeno si concentra alle quote inferiori a causa della maggior pesantezza rispetto all’azoto; per tale motivo è consigliabile mantenersi ad un livello più basso: la respirazione è agevolata.

Troviamo le frazioni massiche:

Nota: Quando diciamo che la percentuale di ossigeno nell’aria è pari al 21%, non ci riferiamo alla massa, bensì al volume (o alla pressione), quindi è bona norma specificare a quale grandezza ci riferiamo. Infatti dai risultati vediamo che ciascun elemento del miscuglio possiede differenti percentuali in volume, piuttosto che in massa.

Troviamo il numero di moli:

n_TOT= 0,134 Kmol

Analogamente a quanto fatto in precedenza possiamo calcolare le frazioni molari:

Abbiamo quindi trovato la composizione del miscuglio cercata. Osserviamo che si tratta di un gas respirabile (è un aria leggermente più ricca di ossigeno-rispetto al normale 21%).

(3)

(non corretto)

Per calcolare c_v3,non vale lo stesso ragionamento, in quanto ci stiamo riferendo ad un miscuglio che ha una percentuale di ossigeno diversa dal 21%. (Notare comunque che il 29 si trova tramite M_TOT/n_TOT).Proseguiamo invece in questo modo:

Scriviamo l’equazione di stato allo stato fisico finale: P3V3=M3R3T3

ESERCIZIO 3.

Immaginiamo di spingere lo stantuffo di una pompa dal punto A al punto B.

Fig.4 – pompa da bicicletta.

Dati:

V₀=1m³	V₀=1m³	T_B=? T_A=20 °C = 293 K
V₁=2m³	V₁=0	P_B=? P_A=1 bar = 10⁵ Pa
		L_N=?
V_A=3m³	V_B=1m³	(lavoro « netto », ovvero compiuto da colui che spinge)

Fig.5 – grafico del processo.

Nota: la curva è adiabatica (senza scambio di calore), perché ipotizziamo una compressione rapidissima, con la quale l’aria viene spinta fuori dalla pompa, prima di cedere calore. inoltre ipotizzando che il sistema sia isolato termicamente si ha che lo scambio di calore Q = 0.

Risulta che T_B>T_Aperché durante il gonfiaggio avviene un riscaldamento.

(4)

Nota: l’esponente g è dato dal rapporto tra calore specifico a pressione costante e calore specifico a volume costante e nel caso dell’aria vale:

Ora cerchiamo la temperatura finale T_B,ma prima ci serve la massa M:

Nota: osserviamo che durante la trasformazione la massa rimane costante in quanto il sistema è chiuso.

Dall’equazione di stato dei gas perfetti allo stato finale otteniamo:

Dal primo principio della termo dinamica: U₂-U₁= Q-L, ma Q=0 e otteniamo:

Nota: passiamo da uno stato di energia più elevato ad uno inferiore, a spese di un lavoro dall’esterno.

Ma in realtà ciò non è corretto, perchè a spingere sono due elementi:

1. colui che applica la forza sullo stantuffo;

2. l’aria atmosferica (esercita una pressione, dato che non siamo nel vuoto);

Al principio, per mantenere lo stato iniziale, non dobbiamo applicare alcuna forza dall’esterno, in quanto la pressione interna è pari a quella esterna…dovremo in seguito con l’applicazione di una forza esterna, contrastare la “sovrapressione”.