COMFORT TERMOIGROMETRICO—TEORIA DI FANGER

Daniela Ternelli, matr. 132538. 15/12/’00, ore 10:30

Analizzando l’equazione di bilancio nelle sue linee essenziali,anche se vista nella sua espressione più completa, consente di individuare tre valori fondamentali per la temperatura, ossia T_i, la temperatura interna del corpo, T_cl, la temperatura esterna, T_a, la temperatura dell’aria, due coefficienti di scambio I_cl, che determina la resistenza dovuta al grado di vestitura, e a=(h_c + h_r), ossia il coefficiente globale di scambio, convettivo e radiante, e due flussi base, vale a dire il calore metabolico M¢=M-L_P, il metabolismo già ridotto del lavoro polmonare, ed il quantitativo di sudore che giunge sull’unità di superficie nell’unità di tempo:

M-L_P-L_G-U-E_d-E_S-E_R-V_S=R+C

dove M è l’attività metabolica standard, L_P il lavoro muscolare polmonare,L_G il lavoro muscolare,U la capacità di accumulo, E_d-E_S=W_S è un parametro che varia da 0 a 1 e che indica la percentuale di pelle bagnata dal sudore, E_R indica il vapor d’acqua prodotto dalla respirazione e V_S è la potenza dispersa a causa dell’aumento di temperatura dell’aria. Al secondo membro troviamo invece la somma della potenza termica scambiata per irraggiamento (R) e per convezione (C).

Quelli sopra elencati sono gli elementi fondamentali che concorrono a mantenere quasi costante T_i variare dello stato di attività, del tipo di vestiario e delle condizioni microclimatiche ambientali; in condizioni ottimali di regime, il corpo umano non ha bisogno di far ricorso al meccanismo della sudorazione, se si trascura il modesto apporto dovuto alla perspirazione cutanea.

Scriviamo innanzi tutto lo scambio termico convettivo:

C=h_c × f_cl × (T_cl – T_a)

dove il coefficiente di proporzione tra scambio termico e differenza di temperatura, che si dice coefficiente di convezione (h_c), dipende dalla velocità dell’aria, e il suo valore numerico è circa la metà di k_c, ossia il coefficiente di scambio dell’evaporazione; i due fenomeni infatti sono intimamente connessi. f_cl invece rappresenta il rapporto tra la superficie del corpo vestito e la superficie del corpo nudo.

Esempio:

consideriamo un corpo seduto con aria che arriva di fronte

h_c= 8.3 × v^0.6 = 5.47 W/m²K se v= 0.5 m/s

dunque la costante 8.3 sarà dotata di dimensioni, dato che la velocità dell’aria si calcola in m/s (sicuramente una persona sdraiata scambia più calore di una persona seduta o leggermente raccolta).

Quando poi v=0 si dice che l’aria è stagnante, e h_c vale circa 2.73. Di solito un po’ di movimento c’è, o per la velocità dell’aria, o perché è la persona che si muove, e dunque l’aria le arriva addosso (il coefficiente può arrivare anche a 8 o 10).

Esempio:

consideriamo una persona eretta con vento di fronte

h_c= 8.6 × v^0.53 @ 50 W/m²K se v=100 km/h, cioè 100 × 1000/3600 m/s = 27.7 m/s. Quindi questi valori dipendono fortemente dalla velocità dell’aria: con aria ferma h_c vale circa 3, ma l’aria ferma non c’è mai, almeno in teoria perché in condizioni di progetto l’ambiente deve essere dotato di ricambi d’aria (per es. è assolutamente normale da considerare in un ambiente a norma di legge il valore di 0.5 m/s.

La compresenza della “crosta”, costituita dalla pelle e dai vestiti, e contemporaneamente dagli scambi convettivi all’esterno di questa crosta, rendono il problema un po’ troppo complicato. Dobbiamo semplificarlo per arrivare ad un’equazione unitaria.

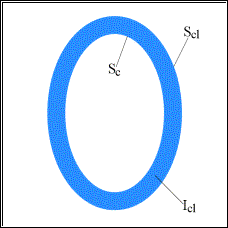
Fuori dell’ovoide, che rappresenta il nostro corpo, avviene il fenomeno della convezione e dell’irraggiamento; ma strutturalmente, dal punto di vista elettrico, la situazione si potrebbe descrivere così:

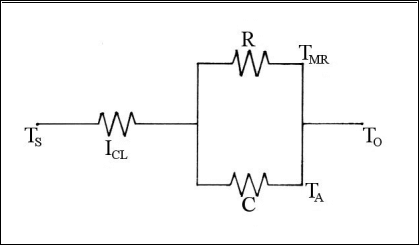
dove T_S è la temperatura superficiale del corpo, I_CL la resistenza termica dovuta ai vestiti (misurata in CLO) e R e C sono rispettivamente il fenomeno radiante e quello convettivo. Le due temperature che otteniamo sono diverse perché abbiamo visto che il fenomeno radiante va a terminare con una temperatura media radiante T_MR, mentre il fenomeno convettivo con la temperatura dell’aria T_A.

Ci piacerebbe ricondurre questa rete elettrica equivalente ad un’unica temperatura che fosse già la media tra T_MR e della T_A, per ottenere la cosiddetta temperatura operante T_O . Quindi noi sostituiamo alla terminazione di questo impianto su due temperature, e quindi su due tensioni diverse, una terminazione unica ed equivalente alla temperatura operante.

Possiamo definirla con questa espressione: T_O = (h_c × t_a + h_r × t_mr) / (h_c + h_r)

Scrivere questa espressione vuol dire linearizzare lo scambio termico radiante in quanto abbiamo osservato che mentre la parte convettiva viene espressa con una diretta proporzionalità tra la quantità di calore scambiato e la differenza di temperatura, viceversa la parte radiante viene scritta così:

R = (3.9 × 10 ^–8) × [T_CL⁴ – T_MR⁴]

Non è certamente un fenomeno ad andamento lineare con la temperatura, perciò sicuramente non può andare d’accordo con un fenomeno lineare come quello convettivo. Si definisce dunque un fattore di proporzionalità lineare, che viene chiamato h_r:

R = h_r × f_cl × [T_CL – T_MR]

Questo coefficiente, definito in questo modo, dipende dalle temperature elevate alla quarta potenza, ma mentre nell’espressione iniziale avevamo una variazione esplicita (cambiavano solo le temperature, la costante numerica rimaneva la stessa) nella seconda invece abbiamo una variazione implicita di h_r a seconda dei valori delle temperature. Questo viene fatto unicamente per definire in maniera compatta la TEMPERATURA OPERANTE e quindi esprimere il problema dello scambio termico tra corpo e ambiente esterno con un unico blocco funzionale che parte da un’unica temperatura e finisce in un’unica temperatura. In realtà questa temperatura dipende in maniera non lineare dalle due temperature: anche se apparentemente sembra una combinazione delle due, il coefficiente h_r contiene a sua volta tali incognite, dunque se ne deduce che la T_MR incide fortemente sulla T_O. Essendo il contributo radiante predominante sul contributo convettivo l’aumento di un grado della T_MR si traduce nell’aumento di due gradi o più della T_O. Ma questi sono dettagli di calcolo; dal punto di vista operativo a noi interessa a questo punto legare la potenza metabolica, e i termini che sono al primo membro, al secondo membro che può venire espresso formalmente in funzione di un’unica differenza direttamente tra la temperatura della pelle umana e la temperatura operante. Con le regole del calcolo dei circuiti elettrici, il secondo membro può essere scritto così:

R + C = a × F_cl × f_cl × (t_s – t_o) , dove a = h_c + h_r è il coefficiente globale di scambio convettivo e radiante, F_cl = 1/1 + (0.155 × I_CL × f_cl × h_c) il fattore di accumulazione del vestiario (che si scrive in funzione del valore di un CLO, che abbiamo chiamato I_CL), t_s è la temperatura superficiale del corpo.

Cerchiamo di sostituire i termini dentro l’equazione in base a quelli che abbiamo fin qui trovato:

· i primi due termini vengono inglobati in M¢;

· cerchiamo di unire tutti quelli che hanno a che fare con lo scambio termico di tipo evaporativo sulla pelle umana: k_c × (0.06 + 0.94 W_s) × (P_sc – P_va), dove W è la percentuale di bagnatura equivalente e l’ultimo fattore rappresenta la differenza tra pressione di saturazione del vapore a temperatura cutanea e pressione del vapore nell’aria;

· Portiamo al secondo membro tutti gli altri termini (legati al volume ventilato polmonare e alla quantità di vapore, proporzionali entrambi al metabolismo): 0.3035 M × (P_sc – P_va) + 0.0167 × M × (T_i – T_a) + a × F_cl × f_cl × (T_s – T_o) + U

Ci sono termini che contengono la P_sc che possono essere portati al primo membro, anche perché sono frazioni del metabolismo. È possibile inoltre definire un nuovo METABOLISMO NETTO, già depurato delle quote di calore che se ne vanno all’aumentare del metabolismo:

M_S = M¢ - 0.3035 M × (P_sc – P_va) – 0.0167 M (T_i – T_a)

Quindi riscrivo l’equazione nella sua forma definitiva:

M_S – k_c × W × (P_sc – P_va) = a × F_cl × f_cl × (t_s – t_o)

1° MEMBRO: il parametro di ingresso primario di tipo metabolico ci dice quanto una persona è attiva, W è la percentuale di bagnatura che ci dice quanto la persona sta sudando (è un valore che non parte da 0 ma da 0.06).

2° MEMBRO: rimane solo il termine legato allo scambio termico attraverso i vestiti, la capacità di smaltimento è governata da quanto siamo vestiti (F_cl), in date condizioni di scambio termico, in particolare v_a è proporzionale alla differenza di temperatura del corpo (che è praticamente invariata) e la temperatura dell’ambiente (che invece è una variabile indipendente).

Se rappresentiamo sul Diagramma Psicometrico, considerando la temperatura T_a (che noi consideriamo T_o) in ascissa, e il Titolo X in ordinata, il luogo dei punti dove l’equazione di bilancio si chiude, scopriamo che per ogni livello metabolico esiste un fascio di rette, fissato un certo grado di attività e un certo livello di abbigliamento (, il GRADO IGROMETRICO, = COST.) In particolare la prima retta non è perfettamente verticale, perché il parametro W non va mai a 0, parte dal valore minimo di 0.06:

Viceversa la percentuale di bagnatura può arrivare al valore massimo che è 1, per cui le corrispondenti temperature di bulbo bagnato vanno da 25° a 35°. Al crescere di W abbiamo situazioni di uguale discomfort fino a quello massimo, che corrisponde alla bagnatura integrale della persona. Dalla pendenza del fascio si comprende che la situazione di comfort a basse temperature è praticamente dipendente dalla sola temperatura, mentre quando questa cresce comincia a risentire in modo più evidente dei valori numerici.

L’ASHRAE ha poi deciso di estendere l’angolo di apertura delle rette nel diagramma, prendendo a sinistra delle rette parallele alla più bassa, e a destra delle rette parallele alla più alta; così è stato costituito il Diagramma Ashrae,dove le curve rappresentano la condizione di contorno:

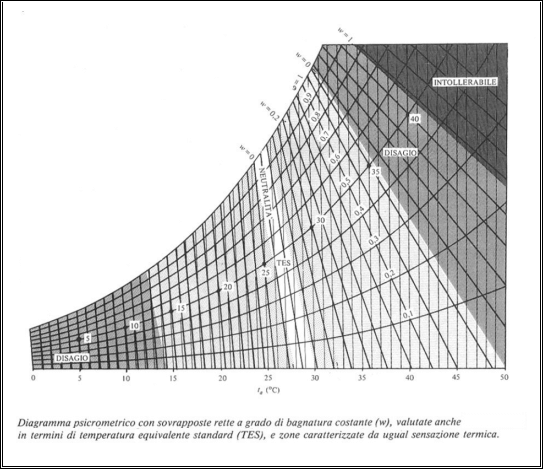
Ad esempio la retta corrispondente alla condizione di studenti che seguono una lezione è quella che ha W = 0.06, perciò in termini di comfort ambientale se mi sposto verso sinistra ho freddo, se mi sposto verso destra ho caldo. Esso in realtà è stato pensato per un lavoratore medio, vestito con giacca e cravatta, che svolge un’attività moderata; non è quindi idoneo alla definizione delle condizioni estreme con persone o poco vestite o molto vestite, che vengono studiate invece dalla Teoria di Fanger. Questo diagramma però è stato criticato perché non sembra corrispondere realmente alle condizioni di comfort, e in effetti la sua derivazione è teorica basandosi sulla solita equazione; regolando un po’ diversamente o l’attività o il grado di vestimento o la velocità dell’aria si ottengono diverse altre varianti che rappresentano condizioni di lavoro diverse.

Quando si parla di progettazione di un edificio però non compare W come parametro, ma piuttosto ci si riferisce al concetto della TEMPERATURA EQUIVALENTE STANDARD o TES, cioè il valore che si ottiene intersecando queste rette a grado di bagnatura costante con la ISO j del 50%. Quando saremo chiamati a fare un progetto l’ente appaltatore ci dirà quali sono i requisiti necessari, ad esempio che la T_O sia compresa tra 25 e 30°C; ma anche se possono variare le situazioni non cambia il diagramma delle TES che è stato ricavato per via teorica (dopodiché caso per caso il committente dirà quali sono i valori che desidera). Perciò per TES non si intende né la temperatura effettiva né la temperatura operante, ma l’unione tra temperatura e umidità.

La teoria dell’Ashrae ha molto successo dal punto di vista commerciale ma è sostanzialmente falsa, perché in verità non c’è uguale comfort quando il grado igrometrico è 0 e quando è 1 (quando è 1 infatti se c’è la temperatura giusta si sta bene, ma se aumenta anche di un solo grado si suda e il sudore non si asciuga); viceversa quando il grado igrometrico è basso l’aria “brucia” i polmoni perché è troppo secca. Quando invece il valore è compreso tra 0.4 e 0.5 all’allontanarsi dalla temperatura di comfort c’è una percentuale di persone insoddisfatte che rimane accettabile. Quindi ciò che ci si propone di fare è trovare la condizione di discomfort che viene sopportata da un’alta percentuale di persone.

Per risolvere questi problemi è nata la Teoria di Fanger; esiste anche uno strumento che rileva i dati termoigrometrici e li elabora secondo tale teoria, il fangerometro. La questione dei calcoli non è altrettanto semplice all’interno della teoria dell’Ashrae, per cui si preferisce utilizzare la più complicata delle due. La base dell’approccio di Ranger non è scientifico-matematica, anzi i suoi risultati sono stati ottenuti da esperimenti in cui il livello di attività non superava 175 W/m² e scegliendo un particolare campione, 1500 giovani studenti universitari: inseriti in una camera a controllo climatico, presso l’università di Copenaghen dove si poteva regolare la velocità dell’aria, la temperatura media radiante delle pareti e il grado igrometrico, vestiti in vario modo e impegnati in attività diverse, dovevano esprimere in una scala compresa tra -1 e 1 il loro grado di benessere:

0 = “sto bene”

-1 = “ho freddo”

1 = “ho caldo”

Essi sono stati sottoposti anche a condizioni di estremo discomfort dalle quali Fanger ricavò tutta una serie di grafici sperimentali che mostrano da una parte come questo voto indicato dagli studenti varia al variare delle condizioni termoigrometriche e dall’altra come varia la percentuale di persone insoddisfatte (è evidente che anche tutti i parametri di cui abbiamo parlato finora hanno una certa influenza su questo voto). Dai risultati sembra possibile affermare che la nazionalità e la posizione geografica non influenzano apprezzabilmente le sensazioni termiche; anche il sesso e l’età hanno un’influenza in pratica nulla (rilevata poco e solo nei bambini), così come la costituzione corporea, le differenze etniche e il ritmo cardiaco. Facendo una media dei voti (M_V) sulla base dei grafici e della teoria, questo voto medio è chiamato P_MV, vale a dire VOTO MEDIO PREVISTO, e consente di individuare un valore numerico preciso che si basa sui test da lui fatti, ma che in ogni caso è pur sempre teorico.

P_MV = 0 → condizioni di comfort

P_MV ¹ 0 → condizioni di discomfort

A sua volta il P_MV può essere associato, sempre su base statistica, alla percentuale d’individui insoddisfatti P_PD: nelle migliori condizioni accade che le risposte positive non superino il 95% del totale, il che significa che è illusorio pensare di realizzare la soddisfazione del 100% delle persone. Dunque Fanger studia soprattutto la quantità d’individui insoddisfatti per un certo spostamento dalle condizioni intermedie, e riesce a normalizzare questa scala di valori in modo da definire che quando –0.5 ≤ P_MV ≤ 0.5 si verifica uno spostamento ancora accettabile, per questo succede che meno del 10% dei soggetti è insoddisfatto (ne deriva la norma ISO 7730/’84). Quindi una situazione in cui il P_MV è compreso in quest’intervallo, per un progettista è una condizione molto favorevole ed è il requisito che normalmente viene dato in Europa nei capitolati d’appalto sulla regolazione degli impianti: P_MV ≤ 0.5.

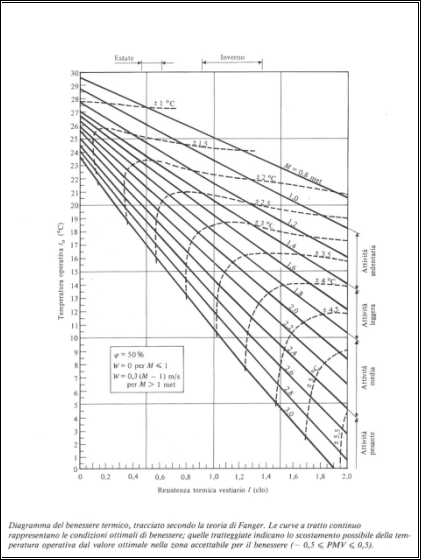
Esempio: una persona vestita con un vestiario standard, che fa un’attività sedentaria normale, ha bisogno di una temperatura intorno a 18°-19°C. Al crescere dell’attività, quando il metabolismo diventa più forte, le curve scendono perché si preferisce lavorare pesantemente in un ambiente freddo.

Il diagramma è disegnato con un grado igrometrico dell’aria del 50%, la v_a è in funzione dell’attività metabolica (nel senso che quando un individuo si muove molto si muove anche rispetto all’aria) e quindi il diagramma è disegnato per una v_a = 0 (v_a = w nel grafico), quando il MET. ≤ 1. In ascissa c’è la resistenza termica del vestiario (in CLO) e le singole rette disegnate sono l’equivalente delle linee a TES costante, cioè le linee di comfort, che rappresentano la situazione ottimale di temperatura in funzione del grado di vestimento e dell’attività fisica. Dunque la parte fondamentale del diagramma di Fanger sono le linee tratteggiate, che mi dicono di quanto mi devo spostare dalla retta che considero per mantenere meno del 10% degli individui insoddisfatti (circa 3 gradi); di fatto questo grafico ha un solo difetto, quello di essere disegnato per un grado igrometrico del 50%.

Esiste però un altro diagramma che mostra il legame tra la temperatura di bulbo bagnato e la temperatura di bulbo asciutto, qui posta uguale alla T_MR; quindi in ascissa c’è la T_O e in ordinata la T_b, temperatura di bulbo bagnato:

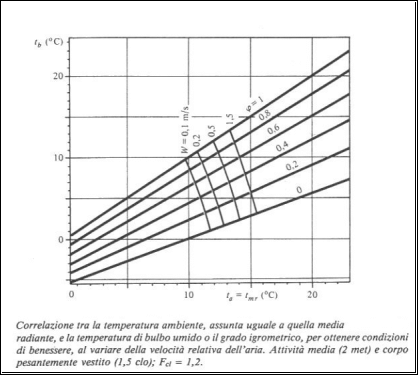
Quindi per mantenere le condizioni di comfort in funzione del grado igrometrico (per es. quando abbiamo j = 0.5, retta con un’inclinazione intermedia) quando è ³ 1 significa che ho un’influenza maggiore di tale termine (T_MR = T_b = T_a); viceversa quando la T_b ≤ T_a perché il grado igrometrico è ≤ 1 le condizioni di comfort si ottengono mediamente a temperature più basse. È lo stesso tipo d’andamento che si vedeva sul diagramma dell’Ashrae, che mostra molto bene la relazione tra temperatura e umidità.

Perciò possiamo incrociare il concetto dell’Ashrae che tanto più l’aria è secca tanto più può essere calda, con il concetto metabolico di Fanger che mi dà le condizioni ottime in funzione della resistenza termica del vestiario e dell’attività metabolica, e mi fornisce la temperatura ideale dell’aria.

Esempio: fissato un certo MET e grado di vestiario, ad esempio MET = 2 e CLO = 1, la domanda che si pone il progettista è se tali condizioni di comfort sono previste dalla norma ISO 7730/’84. Utilizzando il grafico psicometrico per trasformare la temperatura (operante effettiva) di 31°C con j = 0.8 nel corrispondente valore con j = 0.5, che è il valore standard per l’utilizzo del diagramma, si ottiene una temperatura di 34°C che è fuori scala.

Proviamo allora con T_O = 21°C (= 0.8): otteniamo T_O = 21.3°C, ma siccome in prossimità delle linee tratteggiate la tolleranza è superiore a 3°C (è @ 3.1°-3.2°C) posso dire che a 21.3°C mi trovo sul margine della tolleranza prevista dalle norme ISO. Se invece fosse: MET = 1 e CLO =0.5 (cioè se si tratta di persone in abbigliamento estivo), è sufficiente una temperatura di 21°C? Probabilmente no perché l’attività fisica è quasi nulla; infatti, andando a leggere i valori si rileva che la temperatura giusta sarebbe intorno ai 26°C (25.5°C). La tolleranza però in questo caso è molto più ristretta proprio perché il grado di vestimento è basso (1.5°C).