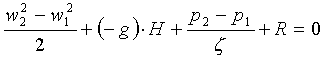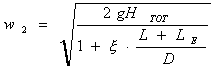Esercizio 2
È dato un serbatoio pieno
d’acqua di volume 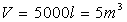 posto ad un’altezza da terra di 15 m e il livello dell’acqua
raggiunge i 17 m da terra. Ad esso è collegato un tubo di lunghezza appunto 15
m e diametro D = 0,1 m e scabrezza relativa di
posto ad un’altezza da terra di 15 m e il livello dell’acqua
raggiunge i 17 m da terra. Ad esso è collegato un tubo di lunghezza appunto 15
m e diametro D = 0,1 m e scabrezza relativa di 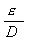 = 0 ,quindi liscio.Si calcoli quanto tempo impiega il
serbatoio a svuotarsi completamente.
= 0 ,quindi liscio.Si calcoli quanto tempo impiega il
serbatoio a svuotarsi completamente.
N.B.:Dal momento che il dislivello disponibile varia da 17 m
a 15 m non è necessario spezzettare troppo il calcolo, ma è possibile
approssimare al livello medio di 16 m.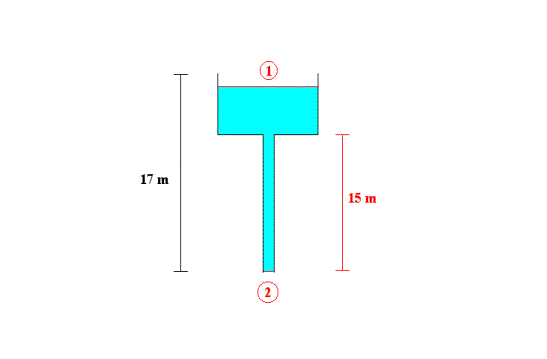
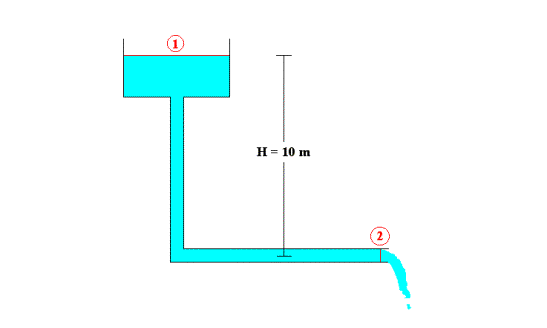
Fig. 3 – Esercizio 2
Per risolvere questo esercizio
devo trovare innanzitutto la portata in volume cioè, 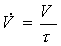 dove
dove 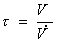 e
e 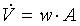 .Così l’area risulta
.Così l’area risulta

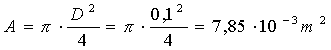
Quindi possiamo
intuire che la vera incognita di questo problema non è tanto il tempo, quanto
più la velocità con cui il recipiente si svuota. Velocità che viene individuata
dalla legge di bilancio di Bernoulli:




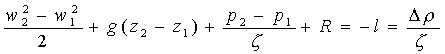
Per semplificare il calcolo scelgo le sezioni 1 (a pelo libero) e 2 (di sbocco).
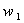 è trascurabile mentre
è trascurabile mentre 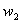 no.Inoltre
no.Inoltre 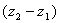 è negativo quindi
risulta -g.
è negativo quindi
risulta -g.
N.B.:La pressione nella
sezione 1 è quella atmosferica ma anche nella sezione 2 la pressione è la
stessa; infatti quella che possiamo percepire con la mano sotto l’acqua non è
la pressione ma una forza, possiede quindi velocità e quantità di moto, non
pressione.
Si ottiene così la formula
notevolmente semplificata:
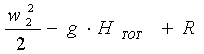 dove
dove 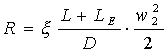
quindi
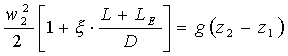
da cui si arriva a
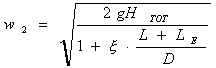
Come si può notare 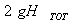 è la velocità torricelliana della caduta di un grave
sotto effetto della gravità. Infatti se un oggetto scorresse senza attrito
viaggerebbe come un oggetto sotto effetto della sola gravità.
è la velocità torricelliana della caduta di un grave
sotto effetto della gravità. Infatti se un oggetto scorresse senza attrito
viaggerebbe come un oggetto sotto effetto della sola gravità.

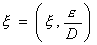 ma essendo la
scabrezza relativa del tubo nulla,
ma essendo la
scabrezza relativa del tubo nulla, 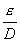 = 0
= 0
quindi il numero di Reynolds risulta: 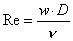 dove n è la
velocità cinetica.
dove n è la
velocità cinetica.
Ora per trovare il valore esatto della velocità devo
inserire valori di tentativo che man mano si diminuisce la differenza di ogni
risultato + ci avviciniamo con precisione al valore esatto.Iniziamo quindi a
inserire valori di tentativo:
Moto a velocità torricelliana 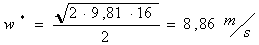
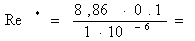 885889
885889
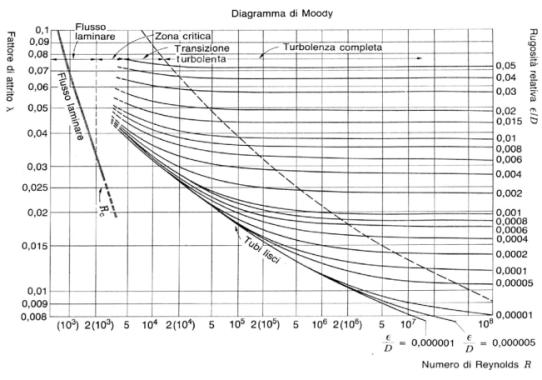
Ora per trovare x utilizzo il diagramma di Moody:
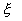 = 0,0118
= 0,0118
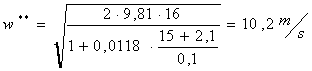
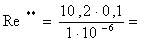 1019915 quindi
1019915 quindi
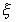 = 0,0117
= 0,0117
Ora possiamo prendere una valore approssimativamente giusto
e calcolare la velocità
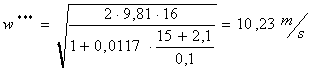
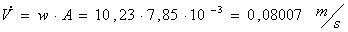
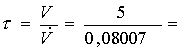 62, 44 s
62, 44 s
N.B.:Più lungo è il tubo più velocemente il recipiente si
svuoterà poiché la lunghezza del tubo è direttamente proporzionale alla
velocità e quindi al tempo che impiega il recipiente a svuotarsi.
Esercizio 3
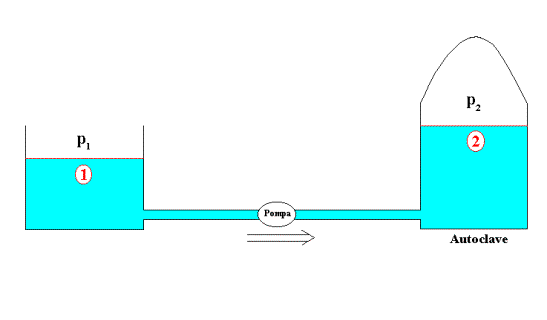
Fig. 4 – Esercizio 3
Utilizziamo come sezioni di studio la sezione 1, a pelo libero, e la 2,
di sbocco,e da qui parte il nostro studio che, come nell’esercizio precedente,
procederà attraverso l’inserimento di valori di tentativo per quanto riguarda
il diametro del tubo.
Si usano in questo caso tabelle di diametri normalizzati dei
tubi :
|
Diametro esterno (mm)
|
Spessore normale (mm)
|
Massa
(kg/m)
|
Diametro
esterno
(mm)
|
Spessore normale (mm)
|
Massa
(kg/m)
|
|
10.2
|
1.6
|
0.344
|
101.6
|
3.6
|
8.76
|
|
13.5
|
1.8
|
0.522
|
108.0
|
3.6
|
9.33
|
|
17.2
|
1.8
|
0.688
|
114.3
|
3.6
|
9.90
|
|
21.3
|
2.0
|
0.962
|
133.0
|
4.0
|
12.8
|
|
26.9
|
2.0
|
1.24
|
139.7
|
4.0
|
13.5
|
|
30.0
|
2.3
|
1.59
|
159.0
|
4.5
|
17.1
|
|
33.7
|
2.3
|
1.79
|
168.3
|
4.5
|
18.1
|
|
38.0
|
2.6
|
2.29
|
193.7
|
5.4
|
25.0
|
|
42.4
|
2.6
|
2.57
|
219.1
|
5.9
|
31.0
|
|
44.5
|
2.6
|
2.70
|
244.5
|
6.3
|
37.1
|
|
48.3
|
2.6
|
2.95
|
273.0
|
6.3
|
41.6
|
|
54.0
|
2.6
|
3.32
|
323.9
|
7.1
|
55.6
|
|
57.0
|
2.9
|
3.90
|
355.6
|
8.0
|
68.3
|
|
60.3
|
2.9
|
4.14
|
368.0
|
8.0
|
70.8
|
|
70.0
|
2.9
|
4.83
|
406.4
|
8.8
|
85.9
|
|
76.1
|
2.9
|
5.28
|
419.0
|
8.8
|
88.7
|
|
88.9
|
3.2
|
6.81
|
|
|
|
Tab.1 – Tubi commerciali lisci
di acciaio per usi commerciali Conforme UNI 4991
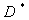 = 26,9 mm
= 26,9 mm
Da qui calcoliamo l’area
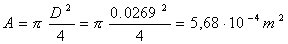
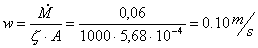
Ora possiamo utilizzare la formula
di bilancio notevolmente semplificata:




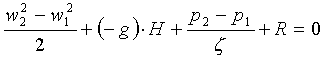
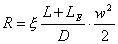
risulta quindi
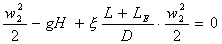
cioè

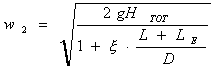

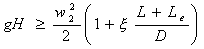
Intanto calcoliamo il numero di Reynolds e la lunghezza
equivalente per accidentalità di imbocco e sbocco:
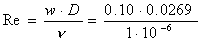 = 2690
= 2690
Il moto è quindi laminare e non
turbolento quindi risulta
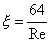 = 0,0237
= 0,0237
Attraverso monogramma otteniamo che
in questo caso 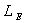 = 1,5 m
= 1,5 m
Ora possiamo sostituire
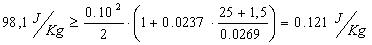
Essendoci troppa differenza tra il
primo e il secondo membro significa che il tubo è troppo grande rispetto alla
capacità richiesta.E’ necessario quindi provare con un tubo di diametro
inferiore.
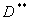 = 13,5 mm
= 13,5 mm
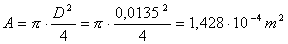
Da qui ricaviamo velocità e numero
di Reynolds:
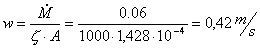
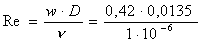 = 5670
= 5670
Quindi il moto è turbolento e
utilizzando il diagramma di Moody
ricaviamo
x = 0,024
Per cui sostituendo otteniamo
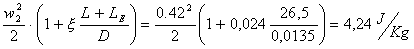
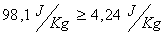
Vi è ancora troppa differenza. A
questo punto utilizziamo il tubo di minore diametro presente in commercio:
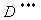 = 10,2 mm
= 10,2 mm
Troviamo area, velocità e numero di
Reynolds
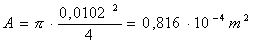
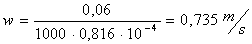
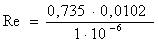 = 7497
= 7497
Essendo moto turbolento utilizziamo
il diagramma di Moody
dove x
risulta circa
x = 0,028
così possiamo sostituire
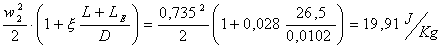
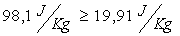
Nonostante ci sia ancora una
rilevante differenza non è possibile procedere oltre poiché questo tubo è il
minore in commercio quindi risulta quello ottimale per il problema.

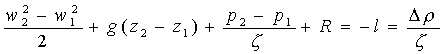
![]()
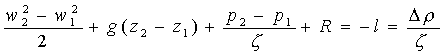
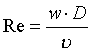
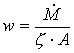
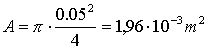
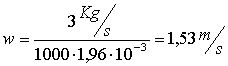
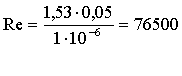

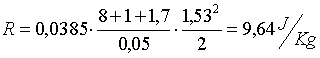

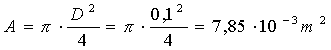


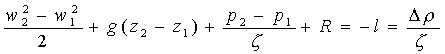
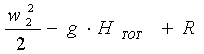
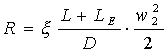
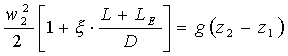
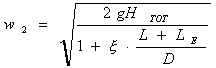
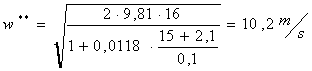
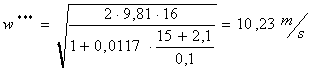
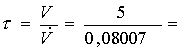 62, 44 s
62, 44 s