(…continua)
Il sistema
idrometrico
Calore
scambiato per convezione:
La dispersione di calore per convezione dalla superficie esterna del corpo vestito può essere così espressa:
![]()
![]()
![]() /
/![]() ( 1)
( 1)
Dove:
C = scambio termico convettivo
![]() = rapporto tra la superficie esterna degli abiti e
quella del corrispondente corpo nudo,
= rapporto tra la superficie esterna degli abiti e
quella del corrispondente corpo nudo, 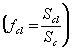
![]() = coefficiente di convezione
= coefficiente di convezione ![]() , valore medio riferito all’intera superficie corporea, il
cui valore dipende dal tipo di convezione. Vale circa la metà di
, valore medio riferito all’intera superficie corporea, il
cui valore dipende dal tipo di convezione. Vale circa la metà di ![]()
![]() = temperatura superficiale esterna dei vestiti
= temperatura superficiale esterna dei vestiti
![]() = temperatura dell’ambiente, dell’aria
= temperatura dell’ambiente, dell’aria
Per la bassa velocità dell’aria
(“aria ferma”) il trasporto di calore avviene per convezione naturale, così che
![]() è funzione della differenza di temperatura (
è funzione della differenza di temperatura (![]() -
-![]() ) ; per velocità più alte, esiste convezione forzata e
) ; per velocità più alte, esiste convezione forzata e ![]() diventa funzione allora della velocità.
diventa funzione allora della velocità.
In condizioni di riposo o in posizione eretta, è stata determinata sperimentalmente la seguente relazione:
![]()
![]() (2)
(2)
Per un corpo seduto frontalmente alla corrente d’aria di velocità relativa v (m/s):
![]()
![]() (3)
(3)
avendo l’aria, in condizioni
normali, velocità relativa v = 0,5 , ![]() sarà 5,47
sarà 5,47 ![]() ; ovviamente se
l’aria o la persona si muovono il risultato cambia perché cambia la velocità
relativa, può arrivare fino a 8 o 10 ; in caso di acqua stagnante vale circa 3.
; ovviamente se
l’aria o la persona si muovono il risultato cambia perché cambia la velocità
relativa, può arrivare fino a 8 o 10 ; in caso di acqua stagnante vale circa 3.
Per un corpo eretto, in moto relativo rispetto all’aria con velocità relativa v (m/s):
![]()
![]() (4)
(4)
nel caso di v = 27,7 m/s (100 ![]() ),
), ![]() =50
=50 ![]() .
.
Per quanto si riferisce al valore della velocità relativa, in assenza di correnti d’aria provocate da cause indipendenti dall’attività dell’uomo, il valore da assumere nei calcoli è quello connesso all’attività stessa.
Scambi combinati
La seconda parte della relazione
di bilancio ![]() , rappresenta
l’uguaglianza tra la quantità di calore sensibile che attraversa gli abiti e
quelle che , per convezione ed irraggiamento, vengono scambiate tra gli abiti e
l’ambiente. Infatti la compresenza della crosta (i vestiti) e dei fenomeni radianti e convettivi rendono il problema
più complicato. Per questo dobbiamo unire e semplificare questi fenomeni e
trovare un’equazione che li comprenda e li unisca insieme, sostituendo una
catena di meccanismi di scambio in serie con un’unica espressione che lega tra
loro il flusso e la forza motrice complessiva.
, rappresenta
l’uguaglianza tra la quantità di calore sensibile che attraversa gli abiti e
quelle che , per convezione ed irraggiamento, vengono scambiate tra gli abiti e
l’ambiente. Infatti la compresenza della crosta (i vestiti) e dei fenomeni radianti e convettivi rendono il problema
più complicato. Per questo dobbiamo unire e semplificare questi fenomeni e
trovare un’equazione che li comprenda e li unisca insieme, sostituendo una
catena di meccanismi di scambio in serie con un’unica espressione che lega tra
loro il flusso e la forza motrice complessiva.
Si arrivano quindi ad ottenere le equazioni:
![]() ,
, ![]() ,
(5)
,
(5)
dove:
![]() = temperatura operante, che definisce
contemporaneamente un valore della temperatura ottenibile come media pesata dei
valori di
= temperatura operante, che definisce
contemporaneamente un valore della temperatura ottenibile come media pesata dei
valori di ![]() e di
e di ![]() ,anche se non dipende in maniera lineare dalle due
temperature; infatti
,anche se non dipende in maniera lineare dalle due
temperature; infatti ![]() incide molto su
incide molto su ![]() , tanto che un aumento di 1°C su
, tanto che un aumento di 1°C su ![]() può corrispondere ad un aumento di 2 o 3 °C su
può corrispondere ad un aumento di 2 o 3 °C su ![]()
![]() = temperatura media radiante dell’ambiente
= temperatura media radiante dell’ambiente
![]() = coefficiente di irraggiamento
= coefficiente di irraggiamento
![]() = coefficiente
di adduzione ottenibile come somma di
= coefficiente
di adduzione ottenibile come somma di ![]() e di
e di ![]() , quindi dello scambio convettivo più quello radiante
, quindi dello scambio convettivo più quello radiante
La situazione può essere così raffigurata:
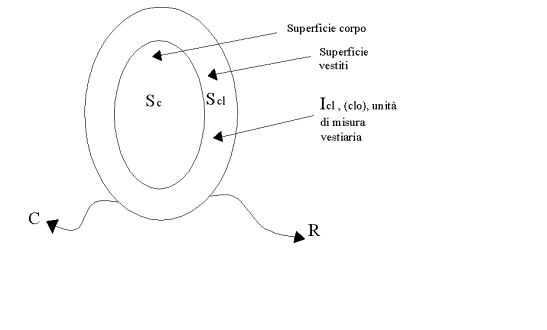
Dal punto di vista elettrico la situazione si può rappresentare così:
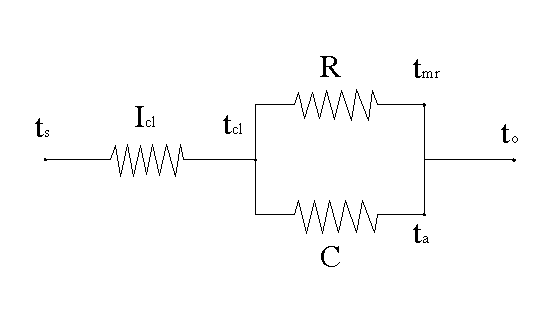
dove:
R = calore scambiato per irraggiamento dalla superficie esterna del corpo vestito
![]() = temperatura superficiale del corpo
= temperatura superficiale del corpo
![]() = unità di misura vestiaria (CLO)
= unità di misura vestiaria (CLO)
Si giunge quindi ad avere che :
![]() (6)
(6)
quindi,
R + C = ![]() (7)
(7)
R + C =![]()
![]() (8)
(8)
Semplificando ulteriormente :
R + C =![]()
![]()
![]() (9)
(9)
Dove:
![]() = coefficiente che tiene conto della diminuzione di
temperatura superficiale connessa con il passaggio del calore attraverso gli
abiti, rappresenta in pratica l’incremento di resistenza termica prodotto dalla
resistenza dei vestiti
= coefficiente che tiene conto della diminuzione di
temperatura superficiale connessa con il passaggio del calore attraverso gli
abiti, rappresenta in pratica l’incremento di resistenza termica prodotto dalla
resistenza dei vestiti
![]() = 1/(1+0,155
= 1/(1+0,155![]()
![]()
![]() )
)
In questo modo siamo quindi in grado di sintetizzare tutto in un’equazione, riuscendo a ricavare le rette di isoriscaldamento di un corpo per cercare di ottenere situazioni di confort.
Tornando
alla relazione di bilancio ![]() , la si può così trasformare:
, la si può così trasformare:
![]() (10)
(10)
dove:
![]() = parte
dell’energia M liberata dai processi ossidativi nel corpo umano per unità di
tempo (in corrispondenza ad un generico livello metabolico) convertita in
calore corporeo interno (il resto viene convertito in potenza meccanica interna
= parte
dell’energia M liberata dai processi ossidativi nel corpo umano per unità di
tempo (in corrispondenza ad un generico livello metabolico) convertita in
calore corporeo interno (il resto viene convertito in potenza meccanica interna
![]() ed esterna
ed esterna ![]() ; alcuni autori suggeriscono addirittura di valutare in
maniera univoca il termine M-
; alcuni autori suggeriscono addirittura di valutare in
maniera univoca il termine M-![]() -
-![]() , attribuendogli convenzionalmente il valore
, attribuendogli convenzionalmente il valore ![]() =0,9 M).
=0,9 M).
![]() = temperatura all’interno del corpo
= temperatura all’interno del corpo
La somma
algebrica del calore metabolico con i termini proporzionali ad M,
rappresentanti il calore sensibile e latente connesso con la respirazione,
consente la valutazione del calore metabolico che , in condizioni di regime,
attraversa la superficie cutanea: tale grandezza viene usualmente indicata con
la lettera ![]() (metabolismo netto). Si giunge quindi alla seguente formula:
(metabolismo netto). Si giunge quindi alla seguente formula:
![]() (11)
(11)
Infatti
ogni volta che M aumenta aumentano anche i termini ![]() e
e ![]() in modo proporzionale
e quindi si semplificano.
in modo proporzionale
e quindi si semplificano.
Posto poi
(0,06 + 0.94![]() )=
)=![]() , dove
, dove ![]() rappresenta il rapporto tra la superficie comunque bagnata e
la totale, indipendentemente dal meccanismo che produce il liquido, in poche
parole la percentuale di sudorazione o il grado di bagnatura, la (11) può
essere rimaneggiata ed espressa nella forma più compatta:
rappresenta il rapporto tra la superficie comunque bagnata e
la totale, indipendentemente dal meccanismo che produce il liquido, in poche
parole la percentuale di sudorazione o il grado di bagnatura, la (11) può
essere rimaneggiata ed espressa nella forma più compatta:
![]() (12)
(12)
In queste
relazioni figurano parametri legati all’ambiente e altri di carattere
fisiologico. I primi sono ![]() ,
, ![]() (o
(o ![]() ),
), ![]() ;al secondo gruppo
appartengono poi M,
;al secondo gruppo
appartengono poi M, ![]() ,
, ![]() e
e ![]() . Esistono poi altri parametri che influenzano indirettamente
queste equazioni, quali ad esempio la geometria e la giacitura del soggetto
(che influiscono su
. Esistono poi altri parametri che influenzano indirettamente
queste equazioni, quali ad esempio la geometria e la giacitura del soggetto
(che influiscono su ![]() ed
ed ![]() , quindi su
, quindi su ![]() ), l’isolamento
termico del vestiario (che influisce sui coefficienti
), l’isolamento
termico del vestiario (che influisce sui coefficienti![]() e
e ![]() ), il movimento dell’aria (che influisce su
), il movimento dell’aria (che influisce su ![]() ), nonché la pressione atmosferica che, se diversa da 101325
Pa (760 mm Hg), influisce sui valori dei coefficienti di trasporto convettivo
di calore
), nonché la pressione atmosferica che, se diversa da 101325
Pa (760 mm Hg), influisce sui valori dei coefficienti di trasporto convettivo
di calore ![]() e di massa
e di massa ![]() .
.
In generale
si può vedere come l’equazione di bilancio, vista nelle sue varie espressioni,
consenta di individuare quegli elementi fondamentali (![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() , il calore metabolico
, il calore metabolico ![]() e il quantitativo Su di sudore che giunge sulla superficie
cutanea nell’unità di tempo) che concorrono a mantenere quasi costante
e il quantitativo Su di sudore che giunge sulla superficie
cutanea nell’unità di tempo) che concorrono a mantenere quasi costante ![]() , al variare dello stato di attività , del tipo di vestiario
e delle condizioni microclimatiche ambientali.
, al variare dello stato di attività , del tipo di vestiario
e delle condizioni microclimatiche ambientali.
Un altro
importante elemento dei parametri ambientali è il contenuto di vapore d’acqua
nell’aria che può essere valutato, in maniera termodinamicamente corretta,
rilevando il valore ![]() della pressione parziale di quest’ultimo nella miscela; noti
della pressione parziale di quest’ultimo nella miscela; noti ![]() e, partendo dalla temperatura dell’aria, la pressione massima
realizzabile
e, partendo dalla temperatura dell’aria, la pressione massima
realizzabile ![]() (tensione di vapore dell’acqua alla temperatura
(tensione di vapore dell’acqua alla temperatura ![]() ), dal loro rapporto si ottiene il grado idrometrico
), dal loro rapporto si ottiene il grado idrometrico ![]() che rappresenta quindi in qualche modo la presenza
percentuale del vapore nell’aria.
che rappresenta quindi in qualche modo la presenza
percentuale del vapore nell’aria.
![]() = costante (13)
= costante (13)
Lo
psicrometro è quello strumento che misura appunto l’umidità , il vapore d’acqua
nell’aria. Esso è costituito da un termometro il cui bulbo è avvolto entro una
garza bagnata: l’aria, lambendo violentemente la superficie bagnata, sottrae
alla stessa vapor d’acqua in misura proporzionale alla differenza di pressione
parziale di vapore (come avviene nel corpo umano), ma il calore latente di
vaporizzazione non viene fornito alla garza dall’interno bensì dall’aria
stessa, che quindi si raffredda
(contrariamente a quanto avviene attorno al corpo umano). Si raggiunge
così una situazione di regime nella quale l’aria fornisce al termometro la
quantità di calore sufficiente e
necessaria a far vaporizzare la quantità d’acqua evaporabile: tale situazione
permane fino a che vi è acqua sufficiente nella garza che avvolge il
termometro; quest’ultimo misura una temperatura inferiore a quella dell’aria
che investe lo strumento, temperatura che viene detta anche di bulbo umido ed
indicata con il simbolo ![]() . L’accoppiamento entro un unico strumento di due termometri,
uno dei quali attrezzato con la garza bagnata, lambiti entrambi dall’aria per
convezione forzata e schermati contro l’irraggiamento termico, da origine ad
uno strumento di misura completo, capace di rilevare ad un tempo
. L’accoppiamento entro un unico strumento di due termometri,
uno dei quali attrezzato con la garza bagnata, lambiti entrambi dall’aria per
convezione forzata e schermati contro l’irraggiamento termico, da origine ad
uno strumento di misura completo, capace di rilevare ad un tempo ![]() e
e ![]() , comunemente noto come psicrometro, quindi di per se
sufficiente a caratterizzare l’ambiente nei confronti degli scambi di calore e
di massa che intervengono con il corpo umano. Attraverso questo strumento si è
infatti riusciti a creare i cosiddetti diagrammi del benessere.
, comunemente noto come psicrometro, quindi di per se
sufficiente a caratterizzare l’ambiente nei confronti degli scambi di calore e
di massa che intervengono con il corpo umano. Attraverso questo strumento si è
infatti riusciti a creare i cosiddetti diagrammi del benessere.
I diagrammi del benessere
Stabilito che il benessere termoigrometrico si realizza in condizioni ambientali, di metabolismo, di vestiario e di velocità dell’aria tali per cui il bilancio del corpo umano risulta verificato senza fare ricorso al meccanismo della sudorazione, ci si pone ora il problema di individuare , da un lato, le condizioni ambientali, di vestiario e di attività che consentono di conseguire la neutralità, dall’altro, la possibilità di associare ad altre condizioni fisiologiche, di vestiario e ambientali, una scala di valutazione del grado di scostamento rispetto alla condizione di benessere.
Entrambi i problemi sopra esposti possono essere risolti solo facendo ricorso ad indagini di carattere statistico. In particolare, l’ASHRAE si è posta il problema di definire un indice capace di valutare lo scostamento dalla condizione di benessere, valutando condizioni moderate con vestiti moderati e lavori moderati, mentre il Fanger individua possibili combinazioni dei diversi parametri caratterizzate dal produrre tutte un ugual stato di benessere , quindi, per ogni condizione di “non benessere” valuta statisticamente la percentuale di individui non soddisfatti, considerando quindi in particolare condizioni non moderate.
Metodo ASHRAE
Riprendendo
il discorso relativo alla funzione termoregolatrice svolta dal meccanismo della
sudorazione e all’importanza che per lo stesso riveste il valore della frazione
di superficie cutanea bagnata![]() , o più in generale
, o più in generale ![]() , si può pensare di associare a ciascun valore di tale
parametro un grado di benessere che, naturalmente, parte dal vero benessere per
, si può pensare di associare a ciascun valore di tale
parametro un grado di benessere che, naturalmente, parte dal vero benessere per
![]() =0 per allontanasi sempre di più da tale condizione man mano
che
=0 per allontanasi sempre di più da tale condizione man mano
che ![]() cresce: tutto ciò è stato fatto dall’ASHRAE che, dopo aver
tracciato sul diagramma psicometrico le linee a
cresce: tutto ciò è stato fatto dall’ASHRAE che, dopo aver
tracciato sul diagramma psicometrico le linee a ![]() = cost., si è posta il duplice problema di associare ad ogni
retta un valore numerico di facile comprensione e quindi di collegare la scala
numerica così ottenuta ad una scala qualitativa delle sensazioni.
= cost., si è posta il duplice problema di associare ad ogni
retta un valore numerico di facile comprensione e quindi di collegare la scala
numerica così ottenuta ad una scala qualitativa delle sensazioni.
Il primo
risultato è stato conseguito attribuendo a ciascuna retta ![]() = cost. il valore della temperatura di bulbo asciutto
corrispondente all’intersezione della retta stessa con la linea a umidità
relativa costante ed uguale al 50%; questo riferimento ha dato origine alla
scala della temperatura equivalente ( o efficace ) standard, usualmente
abbreviata in TES.
= cost. il valore della temperatura di bulbo asciutto
corrispondente all’intersezione della retta stessa con la linea a umidità
relativa costante ed uguale al 50%; questo riferimento ha dato origine alla
scala della temperatura equivalente ( o efficace ) standard, usualmente
abbreviata in TES.
Individuati
così il parametro e la corrispondente scala di valutazione, rimaneva il
problema di coprire tutto il campo del diagramma psicometrico, in quanto alla
condizione di benessere ideale a ![]() =0 corrisponde TES = 25°C, mentre a
=0 corrisponde TES = 25°C, mentre a ![]() = 1 corrisponde TES = 41°C; l’ASHRAE ha ritenuto opportuno
estendere il campo tracciando sul diagramma delle rette parallele alle due
estremità.
= 1 corrisponde TES = 41°C; l’ASHRAE ha ritenuto opportuno
estendere il campo tracciando sul diagramma delle rette parallele alle due
estremità.
L’area più
prossima alla linea TES = 25°C rappresenta la zona di neutralità termica e può
quindi essere considerata come zona di benessere termico; questa condizione
viene per altro estesa a comprendere anche le due aree che la affiancano (tra i
13 e i 36°C TES) e che corrispondono a sensazioni termiche di leggero caldo e
di leggero fresco. Temperature efficaci inferiori a 13°C e superiori a 36°C
corrispondono a sensazioni di disagio. L’area
al di sopra della linea ![]() = 1 comprende poi situazioni microclimatiche tollerabili solo
per brevi periodi di tempo. Codesta scala è valida per individui in attività
sedentaria (1 met) e vestiti con abiti leggeri, bassa velocità dell’aria,
temperatura delle pareti prossima a quella dell’aria (
= 1 comprende poi situazioni microclimatiche tollerabili solo
per brevi periodi di tempo. Codesta scala è valida per individui in attività
sedentaria (1 met) e vestiti con abiti leggeri, bassa velocità dell’aria,
temperatura delle pareti prossima a quella dell’aria (![]() =
=![]() ).
).
Per questo motivo il metodo ASHRAE risulta adatto per regolare un edificio destinato ad uffici, infatti, i 25°C che pone come temperatura perfetta per il benessere non potrebbero mai andare bene in una fabbrica dove si svolgono attività più pesanti.
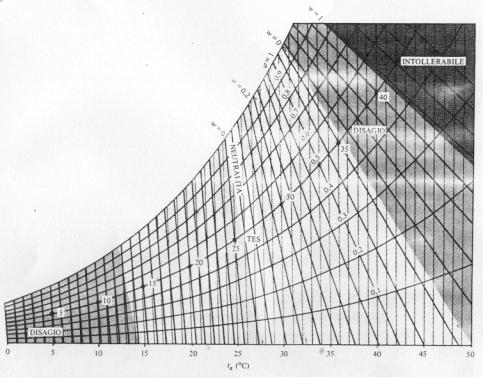
Fig. 1.
Diagramma psicometrico con sovrapposte rette a
grado di bagnatura costante (![]() ), valutate anche in termini di temperatura equivalente
standard (TES) , e zone caratterizzate da ugual sensazione termica.
), valutate anche in termini di temperatura equivalente
standard (TES) , e zone caratterizzate da ugual sensazione termica.
Il metodo Fanger
In alternativa, e tenendo conto della variabilità di un più elevato numero di parametri microclimatici, è possibile determinare le condizioni di benessere secondo il criterio di Fanger, utilizzando un diagramma simile a quello della Fig. 2. Le curve tracciate su tale diagramma definiscono il luogo dei punti corrispondenti a condizioni di benessere; conseguentemente esse possono venire utilizzate per determinare il valore di un parametro, fissati che siano i rimanenti. Occorre tuttavia precisare che questo diagramma non fornisce indicazioni per condizioni che si discostano, anche di poco, da quelle di benessere.
Infatti il Fanger si è proposto lo scopo di approfondire lo studio limitatamente alle condizioni di benessere termico, accettando quel punto lontano dal confort perfetto, ma che comunque non si trova a disagio.
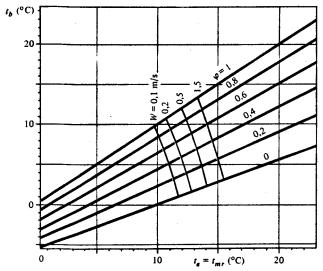
Fig.2.Correlazione
tra la temperatura ambiente, assunta uguale a quella media radiante, e la
temperatura di bulbo umido o il grado idrometrico, per ottenere condizioni di
benessere, al variare della velocità relativa dell’aria. Attività media (2 met)
e corpo pesantemente vestito (1,5 CLO); ![]() =1,2.
=1,2.
Il suo
approccio allo studio dei diagrammi del benessere è stato di tipo sperimentale,
attraverso dei test fatti a sui studenti in una camera climatica. Questi
venivano esposti a condizioni di sovraccarico o insufficienza termici i cui
valori potevano essere associati a quelli di una scala, arbitraria, di valori
in grado di esprimere il grado di insoddisfazione medio degli individui
esposti, nota come voto medio previsto PMV; a sua volta, il PMV può essere
associato, sempre su base statistica,
alla percentuale di individui insoddisfatti. Si verifica così che nelle
migliori condizioni, che corrispondono a quelle che i più considerano il
benessere, la percentuale di risposte positive non supera il 95% del totale, il
che significa che è illusorio realizzare la soddisfazione del 100% degli
individui. Ne risulta -0,5 ![]() PMV
PMV ![]() 0,5 e PPD
0,5 e PPD ![]() 10%.
10%.
Fanger ha
imposto dei limiti, dedotti sperimentalmente, ai valori della temperatura cutanea
e del calore disperso per evaporazione, limiti che corrispondono a condizioni
di benessere .Ovviamente anche il termine di accumulo di energia U è
rigorosamente uguale a zero (poiché ci si trova in uno stato di confort).Si può
quindi dire che il metodo Fanger
risulta più versatile per la progettazione di un microclima in un
ambiente confinato o no. Esso infatti permette, per ogni tipo di abbigliamento
(CLO) e di attività ![]() /
/![]() di calcolare tutte le combinazioni di temperatura
dell’aria (°C), umidità dell’aria (%), temperatura media radiante (°C) e
velocità relativa (m/s) che realizzano il benessere termico per persone in
condizioni di regime stazionario. Va ricordato che queste relazioni sono state
ottenute da esperimenti in cui il livello di attività non superava 175
di calcolare tutte le combinazioni di temperatura
dell’aria (°C), umidità dell’aria (%), temperatura media radiante (°C) e
velocità relativa (m/s) che realizzano il benessere termico per persone in
condizioni di regime stazionario. Va ricordato che queste relazioni sono state
ottenute da esperimenti in cui il livello di attività non superava 175 ![]() /
/![]() ; inoltre il sesso, l’età, la costituzione corporea,
il ritmo cardiaco ecc., hanno un’influenza trascurabile.
; inoltre il sesso, l’età, la costituzione corporea,
il ritmo cardiaco ecc., hanno un’influenza trascurabile.
Per il
progettista diventa così utile poter tradurre quanto sopra esposto in un unico
diagramma che consenta di valutare gli spostamenti dei parametri ambientali dai
valori di benessere, in relazione al grado di soddisfacimento richiesto.
Stabilito (ISO 7730/84) di accettare una percentuale di insoddisfatti pari al
10% degli individui esposti, cui corrisponde un PMV di ![]() 0,5, ne deriva il grafico riportato in figura 3. Tale
diagramma può essere ritenuto di interesse generale anche se in realtà limitato
dai valori
0,5, ne deriva il grafico riportato in figura 3. Tale
diagramma può essere ritenuto di interesse generale anche se in realtà limitato
dai valori ![]() = 0,5,
= 0,5, ![]() = 0 ed U = 0, essendo questi valori usuali all’interno degli
ambienti confinati adibiti a funzioni abitative o terziarie.
= 0 ed U = 0, essendo questi valori usuali all’interno degli
ambienti confinati adibiti a funzioni abitative o terziarie.
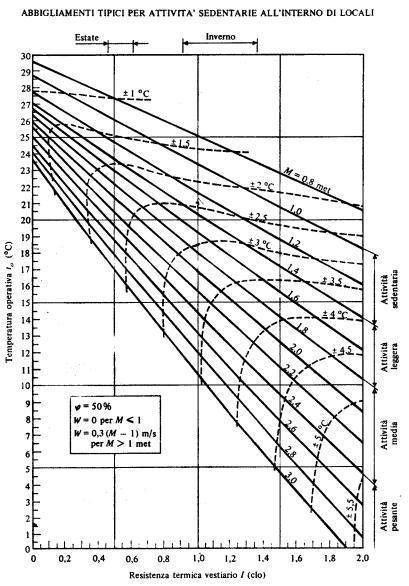
Fig.3.
Diagramma del benessere termico, tracciato secondo la teoria di Fanger. Le curve
a tratto continuo rappresentano le condizioni ottimali di benessere, quelle
tratteggiate indicano lo scostamento possibile della temperatura operativa dal
valore ottimale nella zona accettabile per il benessere (-0,5 ![]() PMV
PMV ![]() 0,5).
0,5).
Esempio numerico
Provo ad incrociare i due metodi o grafici con una stessa situazione; in questo modo riesco a capire , in maniera empirica, come viene valutata una stessa situazione nei due metodi, cercando di individuare per entrambi il grado di benessere.
Posti:
![]() = 0,8
= 0,8 ![]() = 21°C
= 21°C
met = 2 CLO = 1
Nel
diagramma psicometrico scopro che per avere una situazione ottimale di
benessere, quindi posta sulla linea delle TES a ![]() = 0,5, dovrò avere
una temperatura
= 0,5, dovrò avere
una temperatura ![]() = 21,3°C
= 21,3°C
Nel
diagramma di Fanger invece constato di essere in una situazione di conforto in
quanto, dovendo stare a una temperatura di 18°C circa per trovarmi in una
situazione di perfetto benessere, ho un intervallo di ![]() 3 da quella temperatura nel quale sono inclusi i 21°C in cui
mi trovo.
3 da quella temperatura nel quale sono inclusi i 21°C in cui
mi trovo.
La situazione è quindi dal punto di vista idrometrico accettabile.