Premessa

L’aria che esce da un tubo ha la stessa pressione dell’atmosfera.

La pressione atmosferica varia a seconda del peso della colonna d’aia che ci sovrasta. Il peso è dato da

(1)

(forza peso g verso il basso).

Per calcolare la pressione ad una certa quota devo quindi prendere un tubo pieno di aria, valutare quanto pesa e dividerlo per la superficie di base.

 

(divido per A) (2)

Fig.1- tubo di aria.

  

r aria vale normalmente 1,15 kg/m3.

In acqua ogni 10 metri di dislivello danno 1 BAR di pressione.

Fig.2 – Variazione di pressione in acqua.

 

 

I Getti

In un sistema come mostrato in figura si nota che la pressione del getto in uscita

(3)

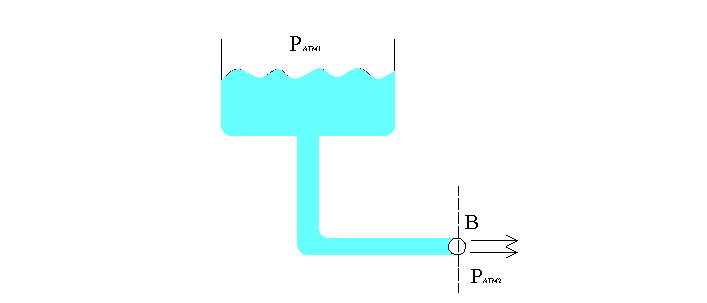
Fig.3 – Serbatoio di acqua.

N.B. In questo caso si utilizza il r aria, (che è diverso dal r acqua =1.000kg/m3). Quando l’acqua si muove le reazioni della statica non valgono più, per questo si usa il r aria che è ferma.

Un esempio pratico di quanto detto finora è il caso di un sistema regolato da un rubinetto.

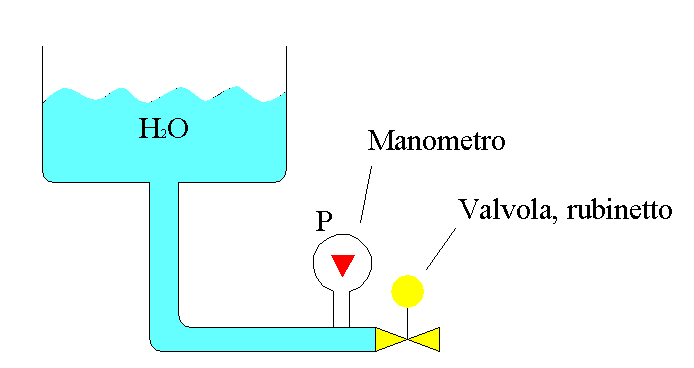
Fig.4 – Sistema regolato da un rubinetto.

Per calcolare la pressione dell’acqua quando il rubinetto è chiuso si utilizza la formula (2) con il r acqua , poiché l’acqua è ferma. Quando invece si apre il rubinetto l’acqua è in uscita, quindi si utilizza sempre la formula (2), questa volta però con il r aria.

N.B. Un fluido che esce da un tubo ed entra a contatto con l’aria ne assume la stessa pressione.

Effetti del getto in uscita

L’acqua in uscita ha una certa velocità W2 che ha come effetti:

1) AZIONE contro chi viene colpito dal getto.

2) REAZIONE che agisce sulle pareti del condotto da cui il getto esce.

 

ESEMPIO 1

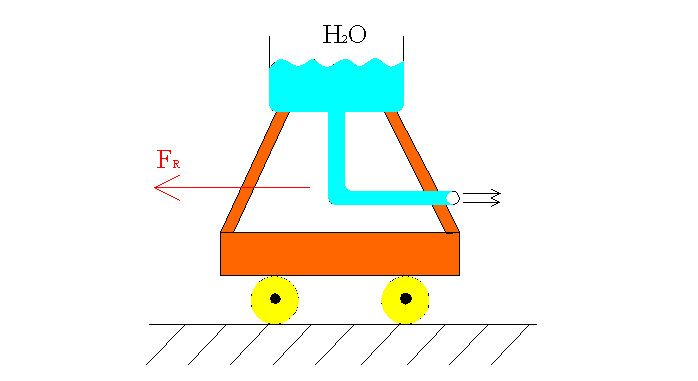
Fig.5 – Carrello che sfrutta il serbatoio pieno d’acqua per muoversi.

La fuoriuscita dell’acqua produce una forza di reazione FR che fa muovere il carrello in direzione opposta a quella del getto.

 

ESEMPIO 2

Fig.6 – Contenitore di aria a pressione.

 

 

 

In questo caso la forza di reazione è dovuta alla fuoriuscita di aria a pressione.

 

ESEMPIO 3

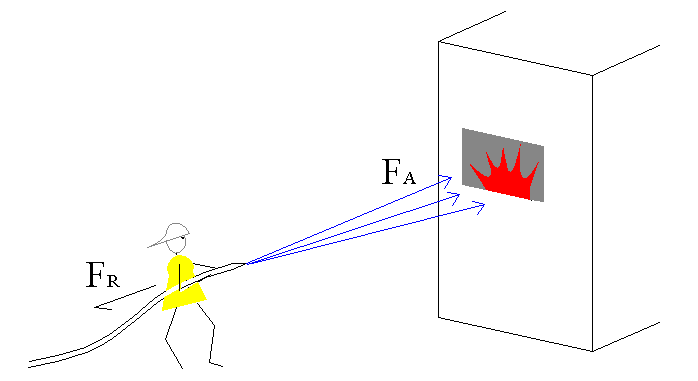
Fig.7 – Esempio del pompiere.

 

La forza FA è una forza attiva, di azione. L’energia cinetica si trasforma in forza.

Il principio di azione-reazione di Newton dice che la forza di azione FA è uguale alla forza di reazione FB.

Un getto scarica alle sue estremità le due forze. Queste sono uguali e contrarie, per cui calcolandone una si riesce a conoscere anche l’altra.

Se il getto incontra una superficie concava fa il giro e torna indietro.

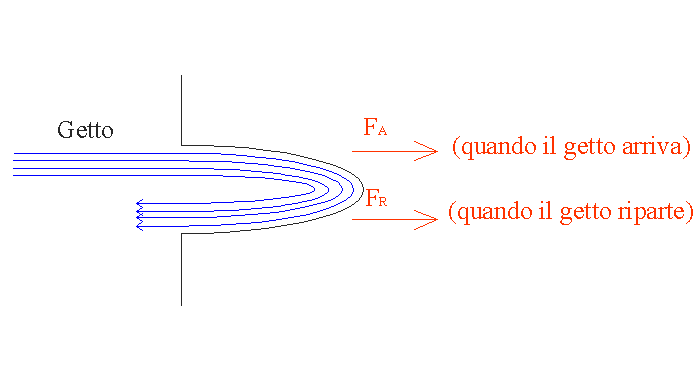
Fig.8 – Getto che incontra una superficie concava.

Come si valutano queste forze?

Si ha un getto di una certa velocità W uscente da un tubo di sezione A.

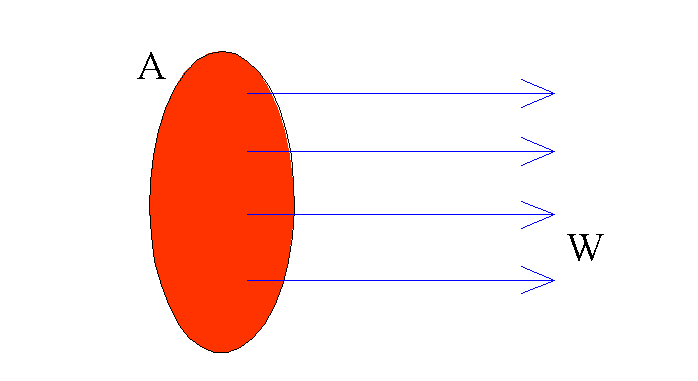
Fig.9

Si può ricavare la portata in massa:

(4)

Per il TEOREMA DELL’IMPULSO (o della quantità di moto) ottengo che:

(5)

Posso effettuare una verifica dimensionale:

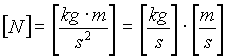
Esercizi

ESRCIZIO 1

Ho una lancia da pompiere come in figura. Si vuole calcolare la forza di reazione FR che il pompiere riceve.

 

Fig.10 – Lancia da pompiere.

Osservando che non si ha né variazione di quota né perdita di carico, utilizzando l’equazione di Bernoulli si ottiene

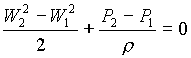(6)

Trascurando W1 si ha

 

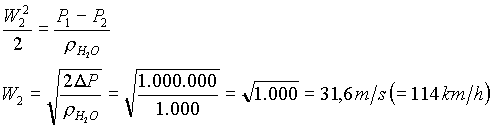
La spinta che viene esercitata su colui che tiene in mano la lancia si può ottenere utilizzandoli nuovo il teorema dell’impulso (5).

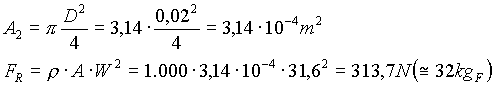
Si può raffinare il calcolo considerando anche W1. E’ necessaria una seconda equazione poiché le incognite sono due. Questa ci è fornita dall’EQUAZIONE DI CONTINUITA’ la quale dice che la portata in massa M1 attraverso la sezione 1 D1 è uguale alla portata in massa M2 attraverso la sezione D2, cioè

(7)

ma essendo l’acqua un fluido incomprimibile vale anche

. (8)

Dalla (7) si ha che

dividiamo per r

(9)

Dalla (9) si ottiene

quindi sostituendo nella (6) si trova

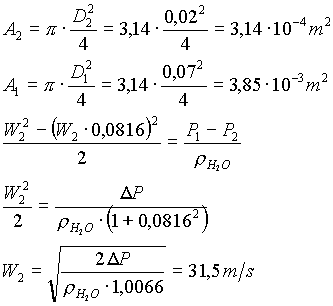
Si può notare che l’errore è minimo. Quando la variazione di sezione è così forte si può infatti trascurare W1.

 

ESERCIZIO 2

Si ha una bomboletta come in figura. Si cerca la forza FA prodotta dal getto.

Fig.11 – Bomboletta di aria.

 

La velocità W1 all’interno della bomboletta è molto bassa rispetto a quella in uscita W2, quindi è trascurabile.

Dal momento che i gas non hanno densità costante, non è possibile utilizzare le equazioni dell’idraulica.

L’aria in uscita cala enormemente di temperatura, quindi la sua trasformazione non è una isoterma ma adiabatica, cioè senza scambio di calore poiché troppo rapida.

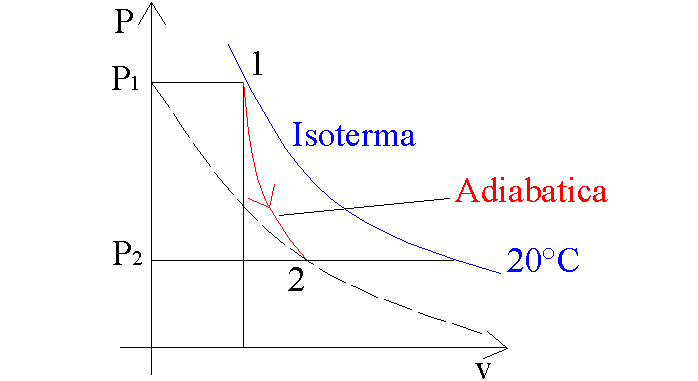
Fig.12

Trasformazione adiabatica:

(10)

da cui

e si ricava v2

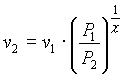. (11)

Dall’equazione di stato dei gas perfetti si ottiene

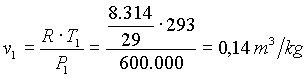
dove 8.314 è la costante universale dei gas, 29 è la massa molare dell’aria e 293 sono i kelvin. Si sostituisce quanto trovato nell’equazione (11), si ha quindi

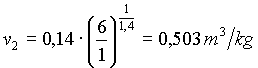
Conoscendo v1 e v2 si possono ricavare r 1 e r 2 con la formula

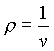(12)

Si ha quindi

Analogamente si può trovare la temperatura dell’aria in uscita T2

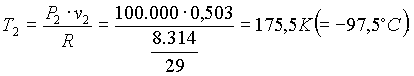
Il problema è risolvibile con il 1° PRINCIPIO DELLA TERMODINAMICA (conservazione dell’energia). Si tratta di un fenomeno conservativo privo di fenomeni dissipativi, non vi sono perdite di carico. Ho quindi una perfetta conversione dell’entalpia in energia cinetica in uscita. Non vi è inoltre differenza di quota, scambio di lavoro né di calore. L’equazione

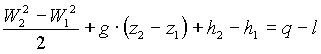(13)

si riduce a

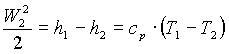
Si può ora trovare la forza prodotta dal getto:

 

Effetto camino

 

 

Fig.13 – Un camino.

E’ un processo di combustione. La temperatura è talmente elevata che la fiamma è luminosa. La fiamma è un processo di combustione.

La parte di calore che fuoriesce dal camino è il 10% dell’energia disponibile. La differenza di temperatura tra l’interno e l’esterno fa "tirare" il camino, quindi tanto più la legna ha potere calorifico (secca e resinosa), più c’è differenza di temperatura e di conseguenza più tiraggio.

Il potere calorifero della legna Pc vale

(14)

e ogni kcal sono 4.187 kJ.

Ogni kg di legna, per bruciare, richiede una certa quantità di aria. Questa è data dal RAPPORTO DI COMBUSTIONE:

Durante la reazione chimica, ossia durante l’ossidazione, vengono prodotti circa 13 (9/15) kg di fumi. Questa massa di fumi va smaltita.

Se il caminetto consuma 5kg di legna all’ora significa che ha bisogno di 50kgaria/h. Di conseguenza la quantità di fumo da smaltire sarà

e la portata in massa in secondi sarà pari a

.

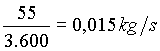Questi valori sono relativi a camini di piccole dimensioni. Un camino di dimensioni maggiori ha una produzione di fumi che si aggira intorno ai 140kg/h.

Per quanto riguarda il dimensionamento dell’altezza h e della sezione della canna fumaria A, bisogna tenere conto che più lungo è il condotto, più ho motore di tiraggio perché c’è differenza di pressione. Per questo motivo si realizzano le ciminiere negli impianti industriali, ma anche per la legge italiana che si basa sulla concentrazione al suolo e no sulla quantità di fumi prodotti.

Riassumendo, più alto è il camino e più alto è il tiraggio. Di fatto però l’altezza è normalmente bloccata negli edifici a seconda dell’altezza di questi ultimi. Quindi si può gestire soltanto la sezione A, sebbene anche per questa si debba fare riferimento ai diametri prodotti in commercio che non vengono progettati al millimetro.

ESERCIZIO

Fig.14

La linea rossa in figura indica una lunghezza che dà perdite senza tiraggio. La linea verde sta ad indicare la lunghezza del condotto il quale non è dritto. b è il coefficiente di perdita o di accidentalità.

Generalmente un camino ben progettato si fa in questo modo:

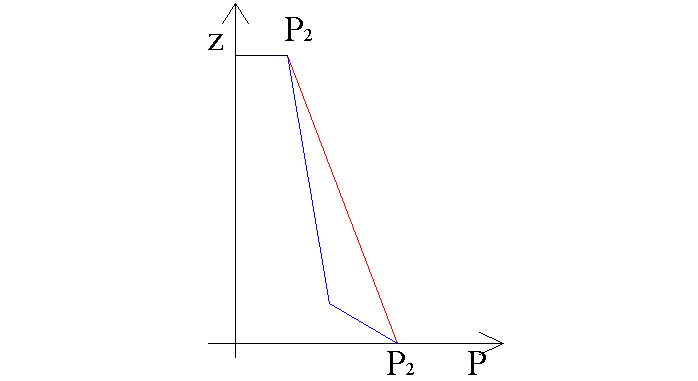
Fig.15

In questo modo se la cappa ha una piccola crepa sarà l’aria della camera ad essere tirata dentro e non il fumo ad uscire. L’intero condotto deve essere in depressione, in tiraggio. La perdita concentrata deve venire il più vicino possibile. Si possono anche montare saracinesche scorrevoli e regolabili o avere bocche di aspirazione più piccole, ma bisogna tenere conto che tutto questo va a discapito del riscaldamento interno.

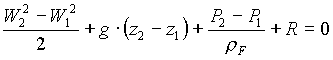
(15)

(16)

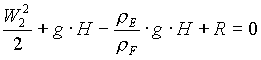
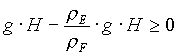
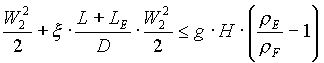(17)

__________________ _____________

ß ß

CARICO MOTORE

Ora basta sostituire i valori numerici per vedere se la disequazione è soddisfatta. Si prova con una cappa quadrata di 15´ 15 (sezione minima secondo la legge italiana). Questa ha area A pari a

.

Si calcola ora la velocità W dei fumi in uscita in funzione di quest’area:

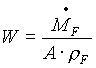(18)

Si usa l’equazione dei gas perfetti per calcolare la densità dei fumi r F:

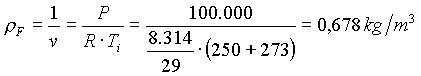
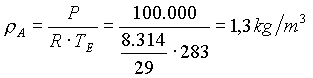
Si sostituisce nella formula (18) il valore trovato:

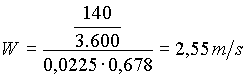
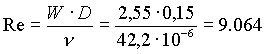® moto turbolento.

Re=Reinolds, n =viscosità. La viscosità dell’aria cambia a seconda della temperatura.

 

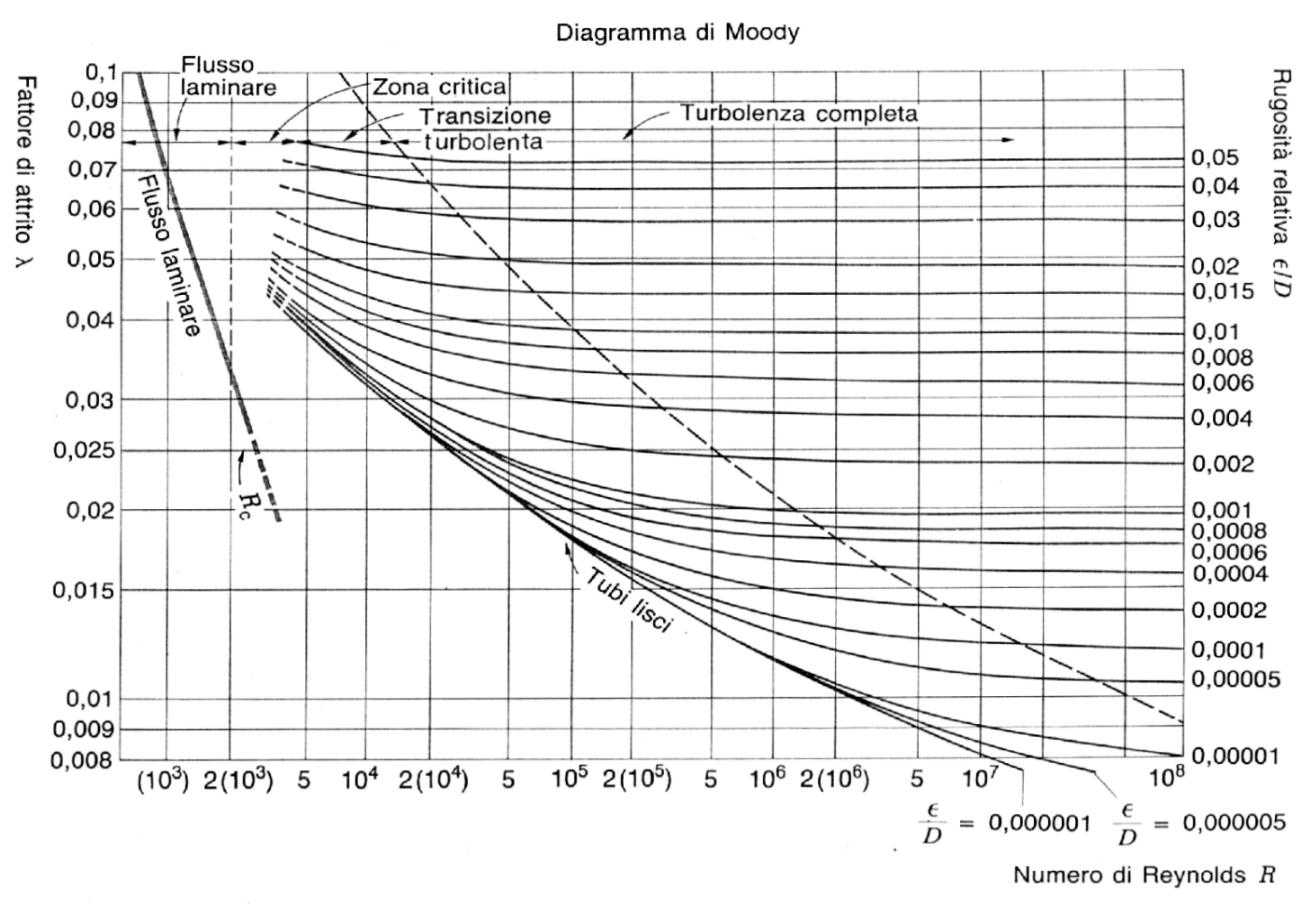
Fig.16

La perdita di carico concentrato si esprime con

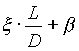. (19)

Si può usare il coefficiente b =1,5.

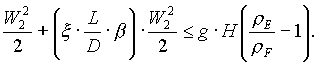(20)

.

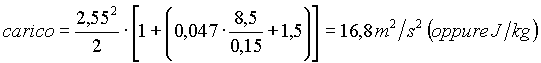
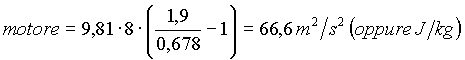Il camino "tira" bene poiché il motore è nettamente superiore al carico. Se il risultato non fosse stato soddisfacente si sarebbe dovuti procedere per tentativi.