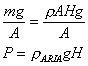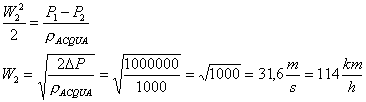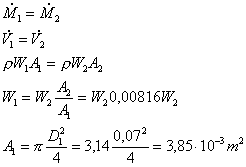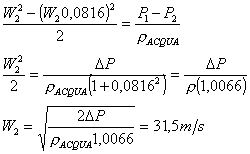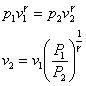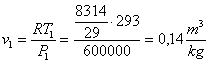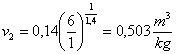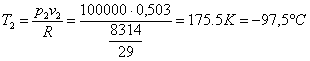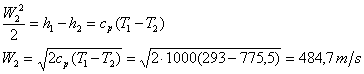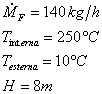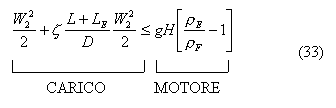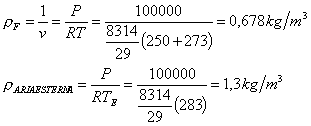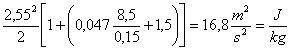Angela Dipino – matr. 132761– Lezione del 19/01/01 –
ora 8:30-10:30
I
getti
Quando l’aria esce
da un tubo ha la stessa pressione dell’atmosfera. La pressione atmosferica
dell’aria varia a seconda del peso della colonna d’aria che ci sovrasta.
Il peso è dato da mg (forza peso verso il basso)
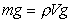 (1)
(1)
Per
calcolare la pressione P ad una certa quota bisogna prendere un tubo
pieno d’aria, valutare quanto pesa e dividerlo per la superficie di base.
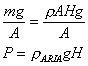 (2)
(2)
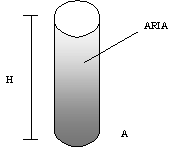
Fig.1
– tubo pieno d’aria.
Nota:
normalmente
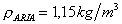 (3)
(3)
Sappiamo
che nell’acqua ogni 10m di dislivello si ha 1BAR di pressione.
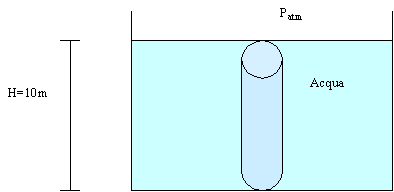
Fig.2
– vasca d’acqua (esempio di misurazione della pressione).
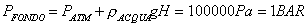 (4)
(4)
In
un sistema come questo
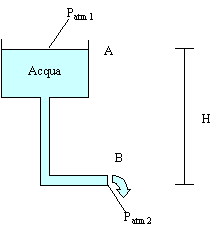
Fig.3
–serbatoio pieno d’acqua collegato ad un tubo.
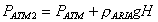 (4)
(4)
Nota:
si usa rARIA anziché rACQUA (
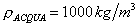 ) perché se l’acqua si muove in un condotto le relazioni statiche non valgono
più. Per questo si deve usare r
dell’aria, che è ferma.
) perché se l’acqua si muove in un condotto le relazioni statiche non valgono
più. Per questo si deve usare r
dell’aria, che è ferma.
Un’applicazione
pratica di quanto detto fin’ora è il rubinetto.
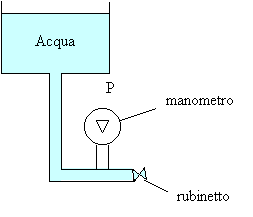
Fig.4
–serbatoio pieno d’acqua collegato ad un tubo con un rubinetto.
QQqQQuando il rubinetto è chiuso l’acqua è ferma e
quindi per calcolare la pressione si usa rACQUA. Se si apre il rubinetto si userà rARIA.
Un fluido che esce da un tubo e va in contatto con
l’aria ne assume la stessa pressione.
EFFETTO DEL GETTO
D’ACQUA CHE ESCE:
L’acqua in uscita da
un condotto avrà velocità W2. Gli effetti sono:
-azione contro
chi viene colpito dal getto;
-reazione che agisce sulle pareti del
condotto da cui esce il getto.
Esempio 1:
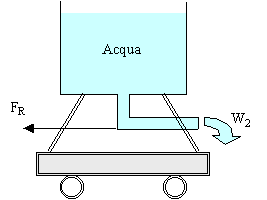
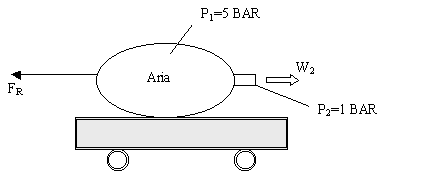
Fig.3
- carrello che sfrutta una sacca piena d’aria per muoversi.
In
questo caso la forza di reazione è provocata dalla fuoriuscita d’aria in
pressione uscente dalla sacca.
Esempio 3:

Fig.6
– lancia del pompiere.
Il principio di azione e
reazione di Newton dice che FR = FA. un
getto scarica quindi alle sue estremità due forze uguali e contrarie.
Nota:
tutte queste valutazioni vengono fatte considerando un caso ideale: il getto
dopo aver prodotto tale forza si va a fermare (non ha più energia cinetica).
Se il getto incontra una
superficie concava fa il giro e torna indietro.
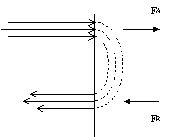
Fig.7
– effetto di un getto contro una parete.
COME SI CALCOLANO QUESTE FORZE?
Ho un getto di velocità
W uscente da un tubo di sezione A.
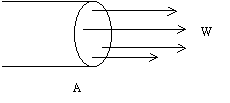
Fig.8
– tubo di sezione A
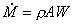 (5)
(5)

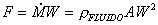 (6)
(6)
Verifica dimensionale:
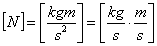


ESERCIZIO 1
Ho una lancia da pompiere.
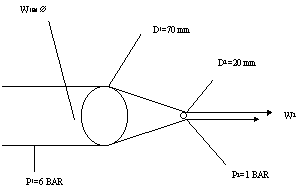
Fig.9
– lancia da pompiere.
Trascurando W1,
osservando che non ho variazione di quota né perdite di carico ed utilizzando
l’equazione di Bernoulli, otteniamo che
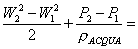 Æ (7)
Æ (7)
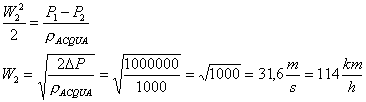 (8-9)
(8-9)
La spinta che viene
esercitata su colui che tiene in mano la lancia può essere calcolata
utilizzando nuovamente il teorema dell’impulso:
Area di sezione:
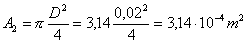 (10)
(10)
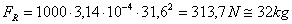 (11)
(11)
Raffiniamo ora il
calcolo considerando anche W1. L’equazione di continuità
dice che la portata attraverso la sezione 1 è uguale a quella che fluisce verso
la sezione 2.
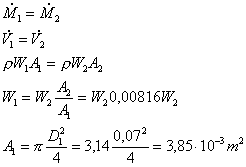 (12-13-14)
(12-13-14)
Tornando all’equazione
di Bernoulli si ha quindi:
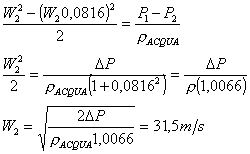 (15)
(15)
Notiamo che trascurando W1
non si compie un errore molto grande. Quando ho una variazione così forte di
sezione posso trascurare W1.
ESERCIZIO 2
Ho una bomboletta.
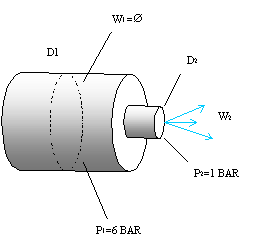
Fig.10
– bomboletta.
W1
è molto piccola rispetto a W2, quindi è trascurabile.
Dal momento che i gas
non hanno densità costante non è possibile in questo caso applicare le
equazioni dell’idraulica fin’ora utilizzate.
L’aria cala
enormemente di temperatura, quindi la sua trasformazione
non è isoterma bensì adiabatica (senza scambio di calore poiché troppo
rapida).
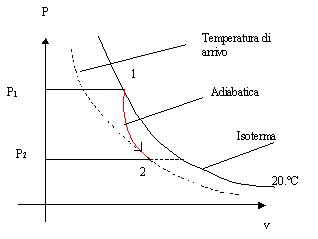
Fig.11
– diagramma pv.
ADIABATICA:
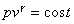 g
per l’aria@1,41
g
per l’aria@1,41
Quale sarà lo stato
fisico finale?
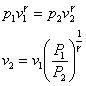 (16)
(16)
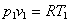 equazione di stato dei gas perfetti
(17)
equazione di stato dei gas perfetti
(17)
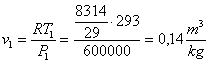 (18)
(18)
Sostituendo in (16):
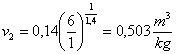 (19)
(19)
Ricavo ora r1
e r2:
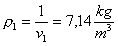 (20)
(20)
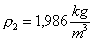 (21)
(21)
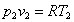 (22)
(22)
Situazione dell’aria
in uscita:
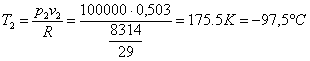 (23)
(23)
Il problema è
risolvibile con il primo principio della termodinamica (conservazione
dell’energia). Si tratta infatti di un fenomeno conservativo privo di fenomeni
dissipativi, non ci sono perdite di carico. Ho quindi una perfetta conversione
dell’energia/entalpia in energia cinetica in uscita.
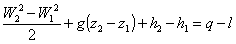 (24)
(24)
W1
è trascurabile, (z2-z1)=0 perché è in
orizzontale, non c’è scambio di calore né di lavoro.
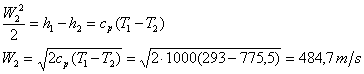 (25)
(25)
L’energia cinetica è
bassa perché è bassa la densità.
Trovo la forza prodotta
dal getto:
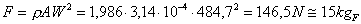 (26)
(26)
EFFETTO CAMINO
Ho un camino.
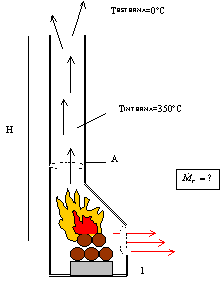
Fig.12
– sezione di un camino.
PROCESSO ESOTERMICO:
il fumo ha una
temperatura così elevata che è luminoso. La fiamma è un processo di
combustione. Solo una piccola parte del colore prodotto fuoriesce dalla bocca
del camino con un fenomeno radiante (10% energia disponibile).
È la differenza di
temperatura che fa tirare il camino. Tanto più la legna ha potere calorifico
(secca e resinosa) e più c’è differenza di temperatura, più c’è tiraggio
perché vengono prodotti fumi molto caldi.
 Potere calorifico della legna
Potere calorifico della legna
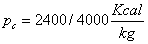 (27)
(27)
Nota:
ogni kcal sono 4187 kJ
Ogni kg di legna,
per bruciare, richiede una certa quantità d’aria (RAPPORTO DI
COMBUSTIONE:
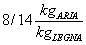 ).
).
Dalla reazione chimica
dei due si producono circa 13 (9/15)kg di fumi. Questa massa di fumi va
smaltita. Se il caminetto consuma 5kg di legna all’ora vuol dire che ha
bisogno di 50kgARIA/h.
Quantità di fumo che
deve essere smaltita:
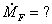
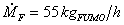 (28)
(28)
Portata in massa in
secondi:
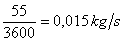 (29)
(29)
DIMENSIONARE L’ALTEZA (h) E LA SEZIONE DELLA
CANNA FUMARIA (A).
Più lungo è il
condotto, più ho motore di tiraggio, perché c’è più differenza di
pressione. Per questo motivo si realizzano le ciminiere negli impianti
industriali. Più alto è il camino più alto è il tiraggio. Di fatto h
è normalmente bloccata negli edifici per abitazione a seconda dell’altezza
dello stesso edificio. Quindi si può gestire solo la sezione.
VERIFICARE IL TIRAGGIO DEL CAMINO
Esempio:
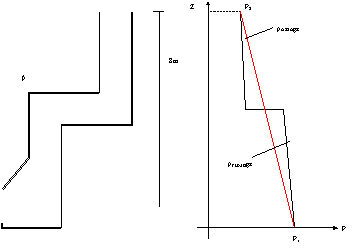
Fig.12
– canna fumaria non dritta.
z:
altezza
P:
pressione aria esterna
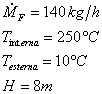
Lunghezza del condotto
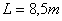
b:
coefficiente di perdita o di accidentalità
Generalmente un camino
ben progettato si fa in questo modo:
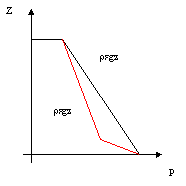
così se la cappa ha una
piccola crepa, sarà l’aria della stanza ad essere tirata dentro la canna
fumaria e non il fumo ad uscire. L’intero condotto deve essere in depressione,
in tiraggio. La perdita concentrata deve avvenire il più vicino possibile. (è
sempre bene a questo proposito montare una saracinesca scorrevole ed avere una
bocca del camino piccola anche se questo va a discapito del riscaldamento).
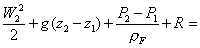 Æ (30)
Æ (30)
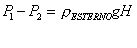 (31)
(31)
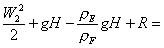 Æ (32)
Æ (32)
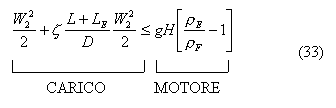
Ora basta sostituire con
i valori numerici per vedere se è soddisfatta. La cappa quadrata è di 15x15 cm
(sezione minima secondo la legge italiana) quindi l’area di sezione sarà
,0225m2.
Calcolo ora la velocità
dei fumi in uscita in funzione dell’area:
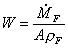 (34)
(34)
uso l’equazione di
stato dei gas perfetti per calcolare la densità

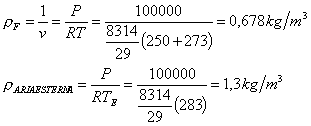 (35-36)
(35-36)
Quindi
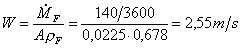 (37)
(37)
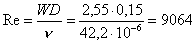 moto turbolento
(38)
moto turbolento
(38)
La viscosità
dell’aria cambia a seconda della temperatura.
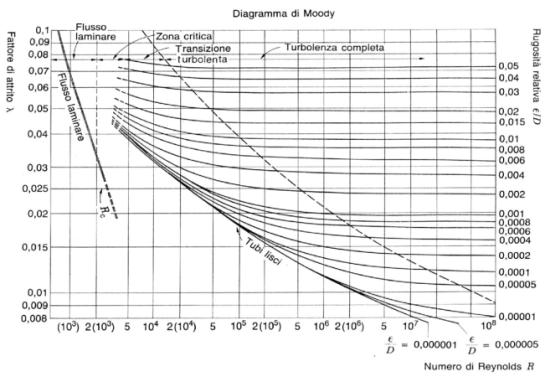
Fig.13
– diagramma di Moody.
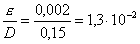 (39)
(39)
La perdita di carico
concentrata si esprime con:
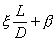 (40)
(40)
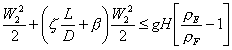 (41)
(41)
CARICO =
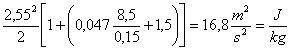 (42)
(42)
Dalla (33):
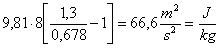 (43)
(43)
Il camino ha quindi un
buon tiraggio perché la forza tirante è nettamente maggiore della forza
tirante, cioè il motore è nettamente superiore al carico.
![]() (1)
(1)