Lorenzo Stagnati-matricola96951-lezione del 11/01/2000- Ore 16:30 18:30
Esercizi di scambio termico per convezione e conduzione
UNIVERSITA’ DEGLI STUDI DI PARMA
Anno accademico 1999-2000
Corso di laurea : ingegneria elettronica
Corso di fisica tecnica
Docente del corso : Angelo Farina
Relazione della lezione di fisica tecnica tenuta il giorno 11/01/2000 alle ore 16 :30-18 :30
INTRODUZIONE
Negli esercizi seguenti vengono posti problemi relativi allo studi dello scambio termico per convezione, conduzione e irraggiamento. Anche se l’argomento di trasmissione per irraggiamento non è ancora stato affrontato nelle lezioni precedenti, è stato considerato per completezza del fenomeno a cui era soggetto il sistema. Verrà quindi riportata una breve spiegazione delle equazioni utilizzate in quanto l’argomento potrà essere maggiormente compreso negli appunti delle lezioni seguenti alla data di oggi.
L’utilizzo delle equazioni usate per risolvere i problemi, richiede la conoscenza e la comprensione degli argomenti affrontati dalla lezione del 21/12/99 fino ad oggi e quindi, salvo particolari eccezioni, la loro spiegazione verranno principalmente omesse. Vengono riportate, invece, delucidazioni riguardo il loro utilizzo e la loro semplificazione dei casi in esame.
ESERCIZIO 1.
Si consideri un condotto rettangolare contenente aria ferma non soggetta a moti forzati. Le pareti di tale condotto sono poste alle seguenti temperature :
- parete n° 1 T1 = 0°C
- parete n° 2 e 4 T2 = 100°C
- parete n° 3 adiabatica
Si chiede di trovare la temperatura Ti dell’aria al centro del condotto, sapendo che il condotto è
lungo L = 1 m
largo L1 = 2 m
alto L3 = 1,5 m
Fig1- condotto rettangolare
Risoluzione
Nel grafico è già stato indicato il moto dell’aria all’interno del condotto dovuto solo alla convezione naturale. Per semplificare la soluzione ci rifaremo alla teoria dei modelli supponendo il sistema come l’equivalente di un circuito elettrico qui di seguito rappresentato
Fig2-schema elettrico equivalente
Le frecce che in normale circuito elettrico rappresentano la corrente, in questo caso simboleggiano il flusso di calore Q, mentre R1, R2 ed R3 sono le resistenze termiche, infine le temperature T1, T2 e T4 rappresentano le tensioni ai capi dei nodi. Dal circuito elettrico così ottenuto è facilmente ricavabile la temperatura Ti come un partitore di tensione. Riduciamo il circuito considerando il parallelo delle resistenze R1 e R3
Fig 3- schema elettrico semplificato
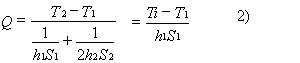
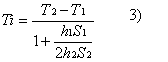
Nell’ultima espressione di Ti si nota che h1 h2 sono dei valori incogniti. Devono essere ricavati con il n° di Nusselt Nu
Nu = C Rab 4)
ma Ra è il n° di Raleigh ed è espresso come
Ra = Gr Pr 5)
anche gli ultime due numeri sono adimensionali e per l’aria in convezione naturale, valgono
Pr = 0,71 6)
![]()
ma in quest’ultima equazione si ritrova la dipendenza da Ti . La soluzione viene affrontata per tentativi imponendo per esempio Ti* = 60° C. A tale valore corrisponde una viscosità cinematica n = 1,89 . 10-5 m2/s, e con b = 1/T = 1/333 otteniamo
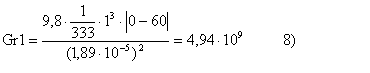
Ra1 = Gr Pr = 3,5 . 109 > 109 9)
quindi il moto risulta turbolento e dai valori tabulati ricavo i coefficienti del n° di Nusselt Nu
C = 0,14
b = 0,333
Nu1 = C Rab =0,14 (3,5 . 109) 0,333 = 197,79 10)
Questo stesso n° può essere anche espresso così
Nu1 = h1 L /l aria 11)
Þ
h1 = Nu1 l aria / L = 197,79 . 0.028 / 1 = 5,54 W/m2K 12)dove l aria = 0.028 W/mK
I calcoli eseguiti valgono solo per la parete orizzontale 1 . Le pareti 2 e 4 sono poste in verticale e quindi soggette a coefficienti diversi
C = 0,13
b = 0,333
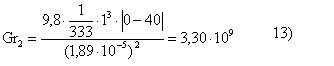
Ra2 = Gr Pr = 3,3 . 109 . 0,71 = 2,34 109> 109 14)
Nu2 = C Rab =0,13 (3,3 . 109) 0,333 = 160,6 15)
h2 = Nu2 l aria / L = 4,5 W/m2K 16)
Ottenuti tutti i valori dei coefficienti di convezione, controlliamo se la stima di Ti*=60° C è approssimativamente accettabile
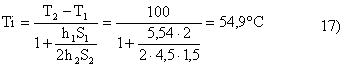
Il valore ottenuto differisce del 9,3% da quello di stima : è un errore troppo elevato e quindi vanno rifatti i calcoli con una nuova temperatura di tentativo Ti** = 54,9° C. Si ottiene una
Ti = 56,7° C
che discosta solo del 3,27% < 5% e quindi accettabile.
ESERCIZIO 2.
Si consideri un condotto circolare dentro il quale scorre dell’acqua ad un temperatura inferiore dell’ambiente. Si vuole progettare la dimensione dell’isolante da porre attorno al tubo affinché non si formi della rugiada, sapendo che :
R1 = 13 mm Tacqua = 5° C
R2 = 17mm T¥ = 20° C
L =1 m
j
¥ = 0,5Fig4- schema di un condotto circolare
Risoluzione
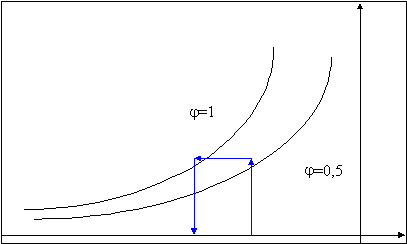
Fig 4- grafico igronometrico
Il problema è di carattere igronometrico. Nel grafico seguente viene raffigurato il raffreddamento a titolo costante. L’orizzontale che intercetta la curva limite individua il punto di temperatura di rugiada Tr =10 ° C. Quindi se l’aria lambisce il corpo con temperatura minore di 10° C si formano delle goccioline d’acqua. La temperatura esterna dell’isolante deve essere Tpe> 10°C
Fig 5- circuito equivalente
Come nell’esercizio precedente rappresentiamo lo schema elettrico equivalente
![]()
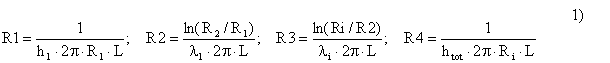
Nella resistenza R4 è stato indicato htot per comprendere anche il fenomeno di trasmissione del calore per irraggiamento. Assumiamo come velocità di progetto dell’aria W = 1m/s, troviamo
![]()
il regime è quindi turbolento e dalle relative tabelle otteniamo
C = 0,023
a = 0,8
c = 0,4
Pr=12,2
Questi coefficienti non compaiono nell’equazione di Dussel Boelter anche perché tale equazione la si usa nel caso in cui è l’acqua a riscaldare l’ambiente. Ora siamo nel caso inverso
Nu1 = C Rea Prc = 0,023 ( 17000) 0,8( 12,2) 0,4=152 3)
Nu1 =h1 D1 /l 4)
Þ
h1 = Nu1 l / D1 =3332 W/m2K ; l = 0,57 W/mK 5)Da questa relazione viene ricavato Q e quindi Tpe , la quale però risulta in funzione di htot. Quest’ultima dipende a sua volta da Ri, cioè l’incognita che stiamo però cercando. Si procede per tentativi fissando un valore commerciale dell’isolante Ri*=20mm. L’esterno del tubo è soggetto al fenomeno di convezione naturale e quindi ricaviamo Gr
![]()
Per un calcolo migliore di b consideriamo la temperatura media dell’aria che lambisce l’isolante cioè
Tm= (20+10)/2= 15° C 7)
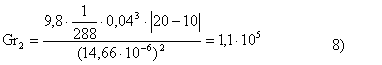
Ra = Gr . 0,71 = 72000 < 109 9)
Dalle tabelle si ottiene
C= 0,53
b= 0,25
c= 0,25
Nu2 = 0,53 ( 72000) 0,8 = 8,7 10)
h2 = Nu l / D1 =5,2 W/m K con l =0,024 W/mK 11)
In prima approssimazione si può trascurare h2, poiché risulta che h1> > h2
Facciamo subito notare che il termine di irraggiamento risulta approssimativamente il doppio di quello di convezione esterna, quindi se sommiamo i due coefficienti risulta
htot = 2 h2 12)
Per verificare ciò, consideriamo l’equazione di scambio termico per irraggiamento
Q= a s 0 [ Tpe4 - T¥ 4] 13)
a= coeff. di assorbimento di corpo nero ; a= 0,9
s
0= coeff. di Stefan Boltzmans 0= 5,67 .10-8 W/m2K4 14)
L’ultima relazione scritta non rappresenta però un equazione lineare e quindi non rappresentabile con una resistenza elettrica. Per linearizzare l’equazione si L’ultima relazione scritta non rappresenta considera un coefficiente hlin tale che
Q= hlin (Tpe- T¥ ) 15)
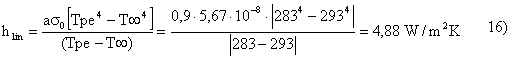
htot = h2 +hlin = 10,8 W/m2K» 2 h2 17)
Infine si ricavano dalle tabelle i valori con
l
i= 0,024 W/mkl
acciaio=75 W/mk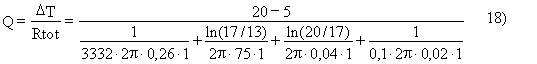
Si può anche esprimere il flusso di calore per metro
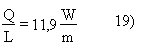
Utilizzando la legge di Ohm, verifichiamo la temperatura Tpe
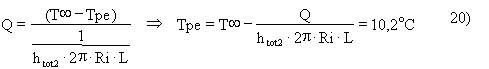
ESERCIZIO 3
Una fabbrica si trova vicino al mare e scarica dei liquami caldi attraverso un tubo che arriva sul fondale. Affinché il liquame non risalga in superficie, la temperatura deve essere minore o uguale a quella del mare. Calcolare la temperatura di uscita del liquame sapendo che
L = 1 km
T1 = 25° C
T¥ = 12° C
R1 = 150 mm
R2 = 180 mm
W= 2 m/s
Risoluzione
Fig 6- schema di scarico liquame di una fabbrica
Per semplicità, consideriamo l’acqua del mare ferma che poi risulta essere il caso peggiore. Infatti si ha solo scambio termico per convezione naturale mentre se fosse forzata si avrebbe un maggior scambio di calore e quindi i liquidi si raffredderebbero di più
Fig 7- schema condotto circolare con relativo modello elettrico
Come nell’esercizio precedente abbiamo considerato un circuito equivalente elettrico dove le resistenze elettriche rappresentano resistenze termiche
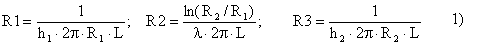
Rtot = R1+R2+R3 2)
![]()
In questo problema si pone il problema che D T non è costante ma varia lungo il tubo
All’inizio vale D T = 25 - 12 mentre alla fine D T = T2-12
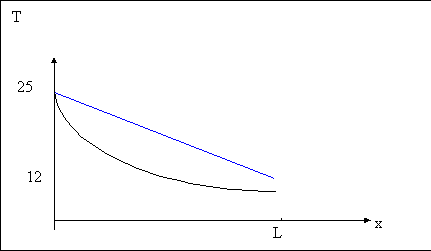
Fig 8- andamento della temperatura nel condotto di scarico
Quindi più il liquame scende in mare e meno scambia calore. Una soluzione potrebbe essere quella di considerare il valor medio anche se la migliore è la media logaritmica
![]()
Infine si può riscrivere
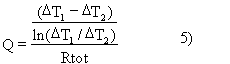
Questa equazione presenta due incognite e quindi è necessaria un’altra equazione. Utilizziamo il 1° principio della termodinamica
(h2 -h1) M= Q ; M = r acqua W A 6)
ed A è l’area di superficie di scambio
A =p R12 7)
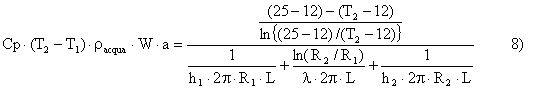
Non è possibile risoluzione analitica, questa è un equazione trascendente e quindi la media logaritmica non è efficace ai fini dei calcoli : per una stima approssimata utilizziamo la media aritmetica che ci permette di calcolare facilmente T2
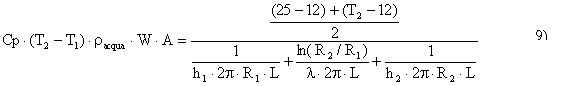
si ricava così T2 :
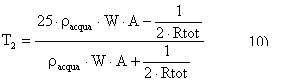
In questa equazione compaiono incogniti anche i coefficienti di convezione. Per ricavarli dobbiamo imporre una temperatura di tentativo T* e verificare se poi risulta sufficientemente esatta. Poniamo
T* =(25+12)/2= 18,5° C 11)
Prendiamo per semplicità le caratteristiche dell’acqua al posto di quelle del liquame e consideriamo
r
acqua=998 Kg/m3n
= 1,1 .10-6l
= 0,6 W/ m KPr = 7,5
Calcoliamo il n° di Re
![]()
Si tratta quindi di un regime turbolento e dato che siamo nelle condizioni di convezione forzata , ricaviamo dalle tabelle che per liquidi raffreddati per Re> 10000
C = 0,023
a = 0,8
c = 0,3
Possiamo ricavare il n° di Nusselt Nu
Nu1 = C Rea Prc = 0,023 ( 136363) 0,8( 7,5) 0,3=540 13)
h1 = Nu1 l / D1 = 4320 W/m2K 14)
Nel caso di h1 bisogna considerare che siamo in convezione naturale e quindi va ricavato non più il n° di Re, ma di Gr
![]()
Ra = Gr Pr = 1,24 . 109 . 0,71 = 8,7 .108< 109 16)
per tale valore otteniamo
C = 0,53
b = 0,25
c = 0,25
Nu2 = C Rea Prc = 0,53( 1,24 . 109 ) 0,25( 0,71) 0,25 = 91,3 17)
h1 = Nu2 l / D2 = 17 W/m2K 18)
l
i= 0,586 W/mK; l acciaio= 45 W/mk 19)Ora che sono stati ricavati i coefficienti di convezione possiamo trovare Rtot
![]()
Non ci rimane che verificare l’esattezza della scelta di T*, cioè di T2
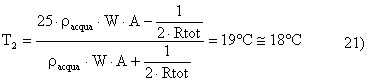
L’errore commesso è del 2,7% e quindi più che accettabile
ESERCIZIO 4.
Consideri una canna fumaria costituita da un tubo di lamiera di acciaio . A che temperatura devono uscire i fumi affinché non si raffreddino troppo e ritornino nella canna fumaria ?
Consideriamo i seguenti dati
H = 5 m
W = 1,5 m/s
T ¥ = 10 °C
D=1m
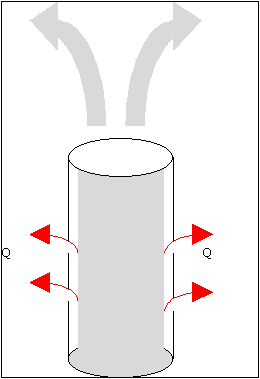
Fig 9- schema di una canna fumaria
Risoluzione
I fumi per salire lungo la canna fumaria devono essere ad una temperatura sufficientemente elevata in modo che il vento in quota li disperda nell’ambiente : questo è un problema di carattere ecologico. Dal punto di vista economico però, risulta al quanto svantaggioso poiché parecchio calore viene portato via dai fumi caldi
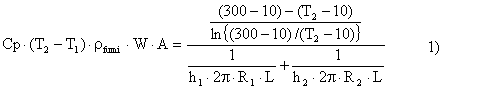
La difficoltà di questo esercizio, che richiede gli stessi calcoli per la soluzione dei coefficienti di convezione, sta nel riconoscere il tipo di convezione presente. Non si tratta infatti di convezione naturale ma in tutti e due i casi, di convezione forzata. Se così non fosse i fumi tenderebbero a scendere, mentre la spinta forzata della caldaia li trascina verso l’alto. In realtà la convezione naturale esiste sempre ma ostacola il moto di risalita di fumi. La risoluzione di questo esercizio è praticamente identica a quella dell’esercizio 3, senza alcuna differenza.