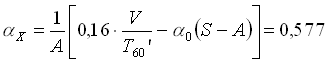
Propagazione sonora in ambienti chiusi.
Se si vuole affrontare lo studio del comportamento di un campo sonoro reale generato da una o più sorgenti poste all’interno di un qualsiasi ambiente chiuso, descrivendo matematicamente come variano i parametri che lo caratterizzano (ad esempio la densità di energia) in funzione delle coordinate spaziali e temporali, occorre tenere conto di un numero così elevato di fattori che senza l’introduzione di opportune semplificazioni l’impresa può risultare ardua o addirittura proibitiva.
Introdurremo allora delle ipotesi basate su considerazioni di tipo statistico che ci consentiranno di raggiungere risultati con buona approssimazione veri a patto però di non allontanarci troppo dalle ipotesi stesse.
1.1 Sorgente Impulsiva
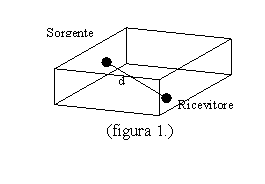
Cominciamo a descrivere il fenomeno considerando una stanza di forma perfettamente regolare, ad esempio un parallelepipedo.

Poniamo al suo interno una sorgente puntiforme e impulsiva, cioè una sfera pulsante che emette dei fronti d’onda perfettamente sferici con uguale intensità in tutte le direzione per brevi istanti di tempo. All’istante t0=0 la nostra sorgente emette un impulso. Prima però che il livello sonoro arrivi sul ricevitore deve percorrere la distanza d fra il ricevitore stesso e la sorgente.
Quindi il primo fronte d’onda emesso arriverà dopo un tempo:
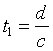
dove c = 343 m/s è la velocità del suono nell’aria. Quando il suono arriva all’ascoltatore, esplica in un istante un livello piuttosto elevato e poi ridecade rapidamente a zero.
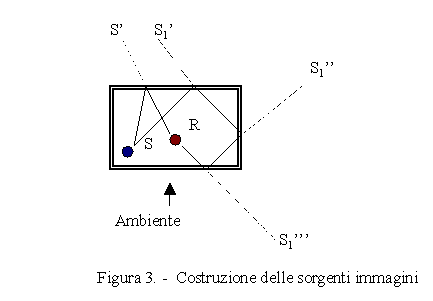
Questo livello chiamato L1 è il livello del suono diretto, cioè del suono che ha percorso la minima distanza possibile tra sorgente e ricevitore senza aver subito alcun fenomeno di riflessione con le pareti. Nella sua espansione però il fronte d’onda sferico incontrerà prima o poi le pareti della sala e a quel punto verrà riflesso. Il suono riflesso raggiungerà a sua volta il ricevitore, ma avrà percorso una distanza maggiore, come se provenisse da una sorgente immaginaria S’ posta al di fuori della stanza e a distanza d2>d1 (vedi figura 3. nel caso monodimensionale). Il suono riflesso una volta arriverà quindi dopo un tempo:
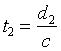
con t2>t1 essendo d2>d. Se il raggio arriva dopo essere stato riflesso più volte si avranno sorgenti immagini del secondo ordine, del terzo ordine e così via.
Inoltre il numero dei possibili cammini esplode aritmeticamente. In un parallelepipedo (6 facce) chiamando ad esempio Ns’ il numero dei possibili cammini dei raggi riflessi una volta abbiamo:
Ns’ = 6
Ns’’ = 6 × 5 = 30
Ns’’’ = 30 × 5 = 150
Nsiv = 150 × 5 = 750
.
.
.
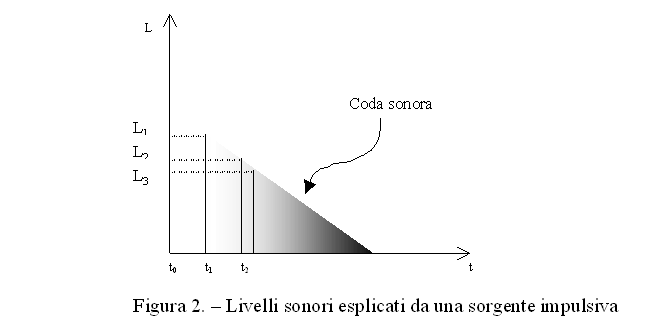
Se visualizziamo in un diagramma il livello sonoro in funzione del tempo ci aspettiamo che accadano due fenomeni contemporaneamente: i tempi ai quali arriva un nuovo raggio diventano via via sempre più fitti a causa della crescita veloce del numero di raggi riflessi, ma la loro intensità si riduce fino a decadere a zero a causa dell’assorbimento. Si ha allora il fenomeno noto come coda sonora o riverberazione.
Con una sorgente impulsiva il fenomeno è molto chiaro. Le sorgenti impulsive non sono però in uso da molto. Tradizionalmente il campo sonoro veniva studiato con sorgenti di tipo stazionario che venivano bruscamente interrotte. Interrompendo l’emissione di energia da parte della sorgente il livello sonoro dopo un certo periodo di tempo decade a zero. In tale periodo il suono non è stazionario ma siamo in presenza di quello che si dice un transiente.
Vediamo cosa succede quando in un ambiente dove c’è silenzio accendiamo in un certo istante t=0 una sorgente di rumore stazionario.
Costruiamo un nuovo diagramma nel quale andiamo a scrivere i livelli sonori che si sviluppano per effetto di tale sorgente. Come prima il fronte diretto arriva al tempo t1 e questo assume il valore L1 , uguale a quello della sorgente impulsiva a patto che la potenza sia la stessa. Però siccome la sorgente non cessa di emettere dopo un millisecondo ma continua ad erogare, il livello rimane costante fino al tempo t2 al quale arriva anche il suono prodotto dalla prima riflessione che va a sommarsi al suono della sorgente diretta. Fatta l’ipotesi che il nostro suono sia rumore incoerente, i due segnali si sommano senza fenomeni di interferenza quindi il livello che si raggiunge è la somma in dB di L1 e L2 dove L1 è il suono dell’onda diretta e L2 è il suono della prima onda riflessa. Dopo di che il livello rimane costante finché non arriva la seconda riflessione la quale fa salire l’intensità ancora di un gradino, questi gradini diventano però sempre più piccoli perché quando ad un suono forte si somma un suono molto più debole il contributo finale tende a diventare trascurabile. Quindi con una serie di piccoli gradini corrispondenti ai singoli arrivi di energia delle successive riflessione si giunge asintoticamente ad un livello costante che chiameremo L0 e rappresenta la condizione di equilibrio energetico di un ambiente.
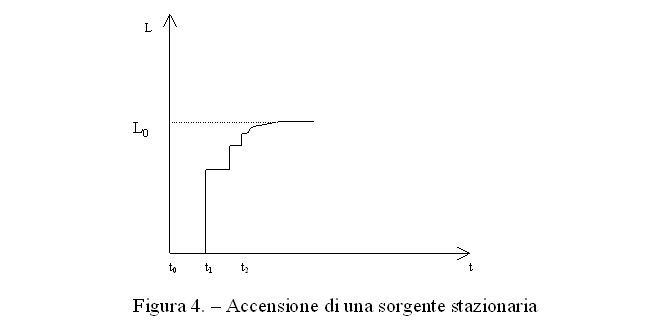
La potenza erogata dalla sorgente, a regime, viene incessantemente assorbita dalle pareti. Quindi il livello costante L0 corrisponde al bilancio tra la potenza che continuamente la sorgente sta immettendo e quella che continuamente le riflessioni sulle pareti stanno togliendo all’ambiente. E’ possibile ricavare matematicamente la situazione di regime ragionando su base energetica ovvero utilizzando come grandezza la densità di energia D.
Poiché in generale D è una funzione del tempo ma anche delle coordinate spaziali lo studio del suo andamento diventerebbe troppo complicato. Facciamo allora delle ipotesi semplificative:
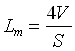 (1.1)
(1.1)
dove S è la superficie totale della stanza e V il suo volume. La stima viene fatta come media aritmetica ponderale delle lunghezze di tutti i possibili percorsi, assumendo come pesi le probabilità che hanno tali cammini di essere effettivamente percorsi. Tali probabilità dipendono dal tipo di diffusione delle pareti a dal fatto che la sorgente abbia o meno una direzione privilegiata di emissione. In ogni caso i nostri risultati saranno tanto più veritieri quanto meno la situazione reale si discosta dalle ipotesi fatte.
Tornando al raggio sonoro il tempo medio che intercorre tra due incidenze successive deve essere:
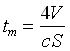 (1.2)
(1.2)
All’interno dell’ambiente le uniche trasformazioni energetiche che avvengono sono l’immissione di energia Es da parte della sorgente e l’assorbimento dell’energia Ea da parte delle pareti. Quindi l’espressione della conservazione di energia può essere scritta come:
Ñ E = Es - Ea (1.3)
Ipotizziamo che in ogni intervallo di tempo infinitesimo dt esiste una frazione di energia circolante dE, anch’essa infinitesima, che incontra le pareti della sala e viene in parte assorbita e in parte riflessa; ammettiamo pure che il processo avvenga senza discontinuità. Allora se l’energia circolante nella sala è per definizione: V× D(t), la variazione di energia sarà data da:
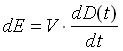 (1.4)
(1.4)
Sappiamo che nel tempo tm l’energia incide una sola volta sulle pareti quindi ne tempuscolo dt l’energia incidente vale:
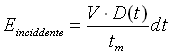 (1.5)
(1.5)
Dobbiamo ora vedere quanta di questa energia incidente viene assorbita e quanta riflessa. Se a i è il coefficiente di assorbimento dell’ i-esima parete, la quantità di energia assorbita vale:
![]() (1.6)
(1.6)
dove 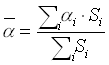 è il coefficiente di assorbimneto medio, cioè la media dei coefficienti di assorbimento di tutte le pareti.
è il coefficiente di assorbimneto medio, cioè la media dei coefficienti di assorbimento di tutte le pareti.
Per l’ipotesi di continuità l’assorbimento risulta distribuito in tutto l’intervallo tm e quindi l’energia assorbita nel tempo dt vale:
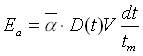 (1.7)
(1.7)
Sostituendo in (1.7) il valore di tm dato da (1.2 ) si ottiene
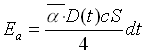 (1.9)
(1.9)
Allora riscrivendo (1.3) come
Es = dE+Ea (1.10)
E sostituendo in (1.10) le rispettive formule trovate per dE e Ea si ottiene
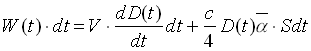 (1.11)
(1.11)
La (1.11) è una relazione generale applicabile sia al caso di sorgente di suono stazionario che di suono variabile nel tempo. Nel caso di suono stazionario dopo un certo tempo dall’accensione della sorgente la densità di regime nell’ambiente raggiungerà un valore di regime Dreg , più precisamente l’energia tenderà ad assumere un valore massimo sopra al quale non è possibile che vada. Se ci mettiamo in un tempo abbastanza lontano dall’accensione della sorgente possiamo considerare
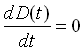
Allora da 1.11 si ha che dopo un certo periodo di tempo
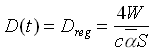 (1.12)
(1.12)
Quindi la densità di regime è direttamente proporzionale alla potenza emessa dalla sorgente e inversamente proporzionale all’assorbimento totale (o potere fonoassorbente)
![]()
Con la relazione (1.12) è facile il calcolo del livello di densità che per l’ipotesi 1 è uguale dappertutto. Troviamo che
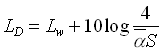 (1.13)
(1.13)
Questa è nota come formula del campo riverberante e ci dice quant’è il livello sonoro prodotto da una sorgente di rumore stazionario in un campo perfettamente diffuso e riverberante. Tale situazione descrive solo in maniera molto approssimata quello che accade in realtà in quanto avvicinandosi alla sorgente sonora è esperienza comune che i livelli sonori aumentano. Effettivamente quello che nelle nostre approssimazioni si può considerare costante in tutti i punti della stanza è il livello del campo riverberante, cioè del suono che ha già subito almeno una riflessione. Per il suono diretto questa semplificazione non è affatto ragionevole. Quindi la formula del campo riverberante è in generale falsa. Ne esiste però una versione modificata che tiene conto di entrambe le componenti, energia del suono diretto ed energia del suono diffuso semplicemente sommandole, nell’ipotesi che la sorgente emetta rumore incoerente che non da origine a fenomeni di interferenza. Il livello di densità totale allora si scrive
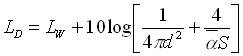 (1.14)
(1.14)
dove a conferma di quanto detto, si vede che il contributo diffuso è lo stesso ovunque, mentre quello diretto varia con l’inverso della distanza al quadrato, quindi è trascurabile se ci allontaniamo e diventa viceversa predominate approssimandosi alla sorgente. Questa formula è nota come formula del campo semi-riverberante e risulta essere una relazione molto semplice che è da tutti comunemente impiegata per valutare il campo sonoro dentro gli ambienti chiusi.
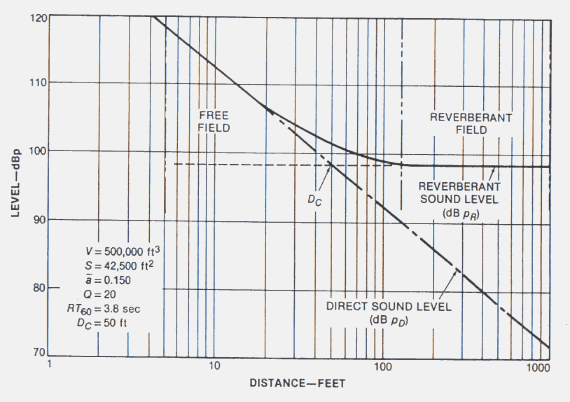
Figura 5. – Andamento del livello del suono diretto e del campo riverberante
Nel grafico di figura 5 è riportato l’andamento del livello sonoro in dB in funzione della distanza dalla sorgente. La linea tratteggiata mostra il decadimento perfettamente rettilineo che si avrebbe considerando solo il suono diretto. La somma dei contributi, diretto e riverberante, tende invece a stabilizzarsi ad un livello che dipende dalla superficie complessiva dell’ambiente e dal suo coefficiente di assorbimento medio. La (1.14) viene scritta in modo leggermente diverso se la sorgente non è omnidirezionale, ma ha delle direzioni privilegiate di emissione. In questo caso si dice che la sorgente è direttiva (ad esempio un altoparlante, la voce di una cantante ecc.) Si definisce allora la grandezza direttività Q, nella particolare direzione q come l’intensità emessa in questa direzione diviso l’intensità media.
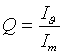
Quindi esiste un coefficiente numerico Q(q ) che mi dice quanto l’altoparlante guadagna rispetto alla sua emissione media in una particolare direzione e normalmente un altoparlante è dotato di una direttività che privilegia l’emanazione in direzione frontale
|
|
Qui a lato è riportato quello che si dice un diagramma di radiazione, o diagramma polare, in cui si legge il fattore di direttività e l’angolo utile di radiazione , ovvero l’angolo entro il quale è massima l’emissione di radiazione sonora. Questo tipo di diagrammi sono ottenuti alimentando l’altoparlante ad una data frequenza e facendolo ruotare rispetto ad un microfono, tenuto fisso ad una assegnata distanza, il quale misura un parametro, in genere la pressione acustica. La lunghezza del segmento che unisce il centro del diagramma polare con un punto qualunque del diagramma stesso misura la differenza Ñ L fra il livello di pressione in quella direzione e il corrispondente livello in direzione dell’asse del disco. |
Figura 6. – Diagramma di radiazione
Considerando la direttività la (1.14) diventa
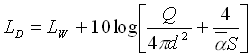 (1.15)
(1.15)
Ovviamente Q può essere maggiore o minore di uno a seconda che ci troviamo entro o fuori dall’angolo di massima emissione. E’ chiaro che essendo l’energia totale fissa se questa è maggiore in una direzione deve essere minore nell’altra. Quindi nella maggior parte delle zone il coefficiente Q è minore di 1.
Introduciamo ora una grandezza fisica importante che è la cosiddetta distanza critica.
Si definisce distanza critica, quella particolare distanza dalla sorgente alla quale il livello del campo sonoro diretto e del campo sonoro riverberante assumono lo stesso valore, si indica con Dc e vale:
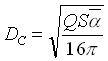 (2.1)
(2.1)
Infatti eguagliando i due termini, campo diretto e campo diffuso si ha
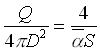 da cui segue subito la 2.1
da cui segue subito la 2.1
Dal punto di vista grafico la Dc rappresenta il punto in cui la curva complessiva del campo riverberante più campo diretto è sollevata di 3 dB rispetto alla retta orizzontale del campo puramente riverberante. In quella posizione dell’ascissa si legge la distanza critica (vedi figura 5).
La distanza critica è estremamente importante in termini di qualità e comprensione del messaggio che viene riprodotto dall’altoparlante. Infatti se ci si trova entro tale distanza dalla sorgente, mi trovo in una situazione dove il suono diretto è predominante sul campo riverberante. Il suono diretto è chiaro, è nitido e porta un’informazione perfettamente intellegibile, viceversa il suono riverberante è confuso. Quindi soprattutto per quanto riguarda la comprensione della parola è importante che l’ascoltatore venga a trovarsi sempre entro la distanza critica dalla sorgente. Questo significa che non è possibile in ambienti molto vasti posizionare un unico altoparlante per esempio al centro e sperare che il suono arrivi chiaro in ogni punto dello spazio. Le possibili soluzioni alla perdita di qualità da parte del suono sono due. Si può puntare un altoparlante molto direttivo direttamente sul pubblico come in figura 7. Così facendo, poiché le persone si possono pensare come un materiale molto assorbente, l’energia viene quasi completamente assorbita e non va ad alimentare il campo riverberante.
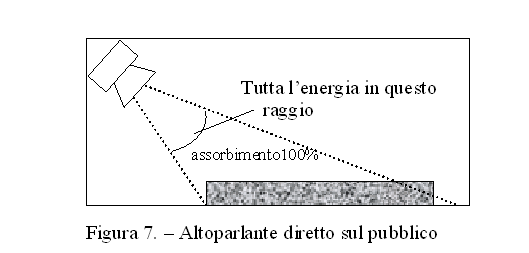
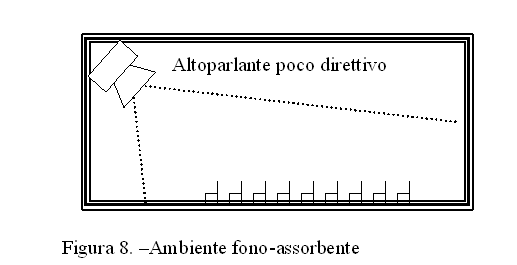
Oppure si può usare una sorgente poco direzionale, a patto però che la stanza abbia un alto coefficiente di assorbimento (figura 8).
Analizziamo meglio cosa succede quando siamo in presenza di suono variabile nel tempo. Supponiamo che una sorgente emetta due suoni, separati da un breve tempo di silenzio.
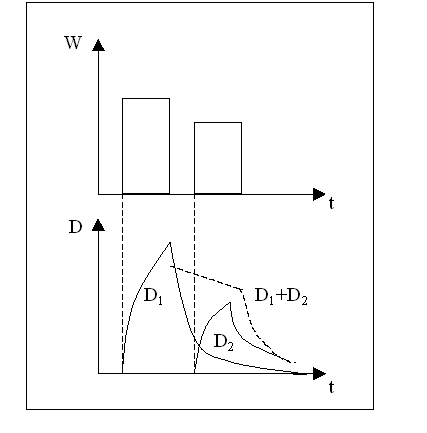
Figura 9. – Potenza e densità di energia di due suoni
Come si vede dai grafici di figura 9 il transitorio di estinzione del primo segnale interferisce con il transitorio iniziale del suono seguente. Questo crea evidentemente un disturbo nel secondo segnale, tanto maggiore quanto maggiore è il transitorio di spgnimento ovvero la riverberazione del segnale che lo precede. Quindi affinché il suono non subisca un’alterazione che lo renda irriconoscibile occorre che la densità sonora del transitorio di estinzione di ciascuno dei segnali acustici discenda velocemente a valori sufficientemente bassi. Tale rapidità in acustica ambientale viene valutata mediante una grandezza denominata tempo di riverberazione, proposta per la prima volta da W. Sabine. Diamone una definizione.
Si dice tempo di riverberazione
Riprendiamo l’esempio della sorgente stazionaria (figura 4).
Giunti a regime, spegniamo la sorgente. La prima energia che viene a mancare è quella del suono diretto. Mentre in accensione però rispetto al silenzio quest’ultima aveva causato un brusco aumento del livello sonoro, ora rispetto al livello di regime alimentato dalla moltitudine di raggi riflessi, l’abbassamento che ne consegue è di entità molto più modesta. Ancora meno rilevante è l’abbassamento dovuto al venir meno del primo raggio riflesso. Il livello tende dunque a decadere a zero con un andamento come in figura 10.
Dopo un primo tratto scalinato la curva di decadimento diviene "liscia" e rettilinea.
Per valutare il tempo di riverberazione seguendo le disposizioni della normativa ISO3382 del 1997 si fa partire il cronometro dopo che il livello è sceso di 5 dB dal livello di regime in modo da evitare il primo tratto "scalinato" e si ferma dunque quando quest’ultimo è sceso complessivamente di 65 dB.
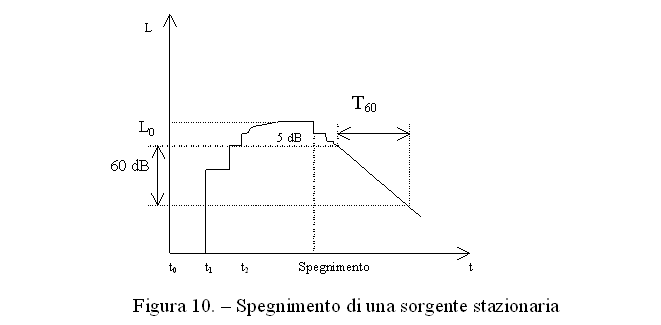
La relazione che lega il T60 alle caratteristiche dell’ambiente è stata trovata sperimentalmente da Sabine e prende quindi il nome di formula di Sabine:
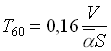 (2.2)
(2.2)
La 2.2 è facile da ricavare anche per via teorica. Infatti consideriamo l’equazione 1.11. Nel momento in cui si spegne la sorgente, W(t)=0 quindi
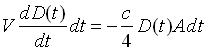 da cui
da cui 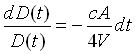 (2.3)
(2.3)
e integrando (2.3) dall’istante t0 di spegnimento al generico t si ha:
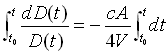 cioè
cioè 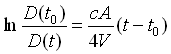 (2.4)
(2.4)
(t-t0) = T60 , dalla definizione 1) D(t)=D(t0)10-6 quindi sostituendo in (2.4)
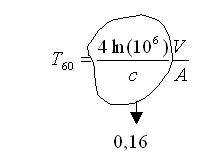
Il T60 ci da direttamente l’effetto percepibile dall’uomo della durata della coda sonora: noi sentiamo un ambiente molto riverberante quando T60>2 sec. e molto asciutto quando T60< 1 sec. Quindi la regolazione del tempo di riverberazione di un ambiente è uno dei principali parametri di progettazione acustica di una sala.
|
Utilizzo |
T60 ottimo (secondi) |
|
Aula piccola |
0,5 |
|
Aula grande |
1 |
|
Cinema |
0,7-0,8 |
|
Teatro dell’opera |
1,3-1,5 |
|
Concert hall |
1,7-2,3 |
Dalla tabella sopra si vede che esiste un tempo di riverbero ottimo a seconda dell’utilizzo della sala..
1.3 Risposta all’impulso e decadimento stazionario
Il problema che ci poniamo ora è quello di calcolare il tempo di decadimento del livello sonoro in un ambiente chiuso mediante l’uso di una sorgente impulsiva. Il livello sonoro in funzione del tempo è dato in figura 2. Il livello complessivo L0 è
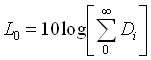
Il livello al generico tempo t è
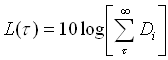
Disponendo di un foglio elettronico, ad esempio Excel si può utilizzare quello che si dice processo di integrazione all’indietro di Schroeder per calcolare il T60.
Si procede così:
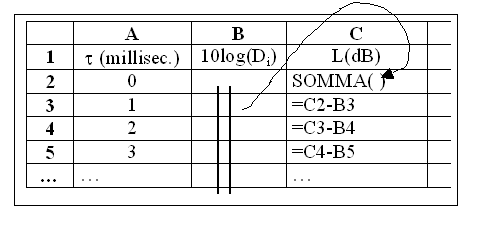
si mettono nella prima colonna (A) i valori discreti del tempo ad esempio in millisecondi, nella seconda colonna (B) si riportano i corrispondenti valori della densità di energia. Sulla prima cella in alto della colonna C si mette la somma di tutti i valori della colonna B, ovvero il livello totale di energia, sulla successive celle , andando verso il basso, si continuano a sottrarre all’energia totale i vari contributi di energia al tempo 1, 2, 3 e così via. Quando sulla colonna C si è scesi di 60 dB allora si va a leggere nella colonna A il corrispondente intervallo di tempo che è esattamente il T60 che stavamo cercando.
Per concludere occorre precisare che oltre al T60 è possibile calcolare il tempo di riverberazione anche considerando intervalli diversi da 60 dB, i più comuni sono 20 e 30 dB. Avremo allora rispettivamente il T20 e il T30 . E’ importante tuttavia non confondersi nel senso che il T30 ha lo stesso valore del T60 e non è la sua metà come potrebbe sembrare. Infatti il T30 è esattamente il tempo che impiega il livello sonoro a decadere di 60 dB, dove però il pedice 30 indica che tale valore deriva da una estrapolazione fatta su una misura di soli 30 dB.
Esercizi
:1.
Dato un ambiente di forma parallelepipeda, conoscendo i coefficienti di assorbimento delle varie pareti ed il livello di potenza erogato da una sorgente posta al suo interno calcolare:
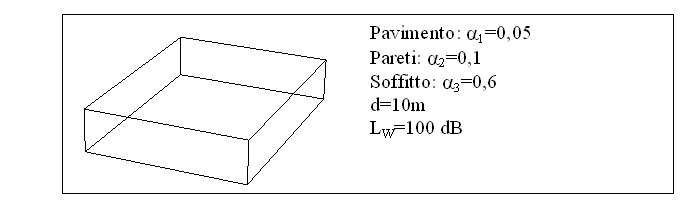
calcoliamo prima di tutto l’assorbimento totale
![]()
il livello del suono diretto vale
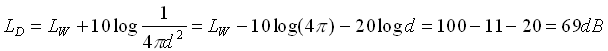
il livello del campo riverberante si trova da 1.13 e vale
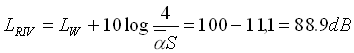
il livello totale è allora
![]()
si vede allora che a 10 m dalla sorgente il livello è dovuto praticamente tutto al campo riverberante, cioè togliendo il contributo del suono diretto il livello scende di pochissimo.
Il rapporto tra campo riverberante e suono diretto vale
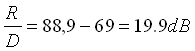
Il tempo di riverberazione è dato da 2.2
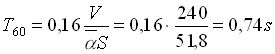
2.
Vogliamo calcolare ill coefficiente di assorbimento di un materiale fonoassorbente.
Abbiamo una stanza di prova, detta camera riverberante, a forma di pentagono irregolare
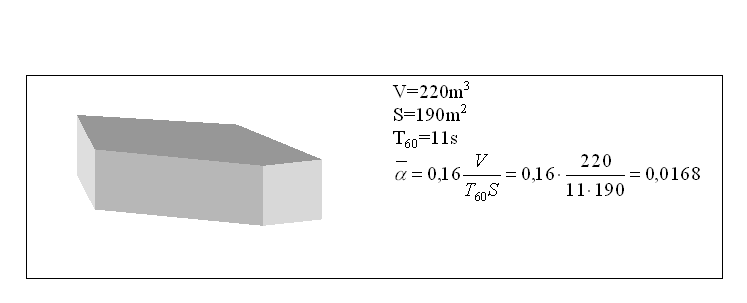
Introduciamo su una parete 10m2 di materiale fonoassorbente. Misuriamo il nuovo T60’ che vale 4s, allora il coefficiente di assorbimento a x del materiale vale
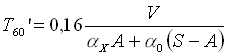 da cui
da cui