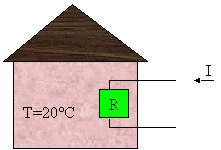
Indicando con L’ il lavoro fornito in forma di energia elettrica, si ha che
![]()
cioè tutto il lavoro viene trasformato in calore per effetto Joule sulla resistenza.
Metodi di riscaldamento per abitazione: bilancio energetico
Lo scopo dell’esercizio è quello di confrontare due metodi di riscaldamento per abitazione dal punto di vista energetico e determinare quale tra i due sia più conveniente.
Si suppone, seguendo i canoni di progettazione vigenti, che la temperatura all’interno dell’abitazione sia di 20°C, mentre la temperatura dell’ambiente esterno sia di –5°C. Si considerano i seguenti metodi di riscaldamento:
Dallo studio di questi due casi si ottengono i risultati seguenti:

Indicando con L’ il lavoro fornito in forma di energia elettrica, si ha che
![]()
cioè tutto il lavoro viene trasformato in calore per effetto Joule sulla resistenza.
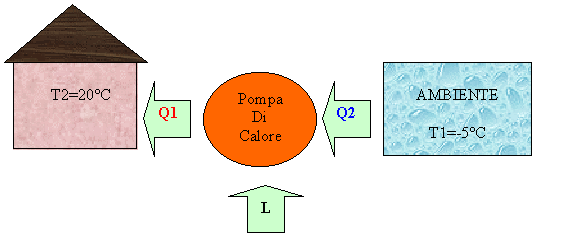
La pompa di calore lavora ciclicamente in maniera reversibile; si ha quindi che il suo coefficiente economico è pari a quello di una macchina di Carnot inversa che lavora tra le due temperature T1= -5°C e T2= 20°C.
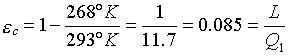
quindi, supponendo che la quantità di energia necessaria al riscaldamento dell’abitazione sia sempre ![]() , si ha che
, si ha che
![]()
di conseguenza si ottiene che
![]()
cioè, il lavoro (quindi l’energia) necessario per scaldare l’abitazione mediante pompa di calore elettrica è 11.7 volte minore di quello fatto usando la resistenza elettrica, ottenendo comunque lo stesso risultato. Bisogna però tenere presente che serve energia elettrica per far funzionare la pompa di calore. A questo punto si vuole determinare la quantità di energia necessaria per produrre il lavoro L (inteso come energia elettrica) utilizzato dalla pompa.
Si supponga di utilizzare una sorgente a Ts=100°C per ottenere lavoro e quindi far funzionare la pompa di calore. Quanta energia sotto forma di calore si deve prelevare da tale sorgente per ottenere lo stesso risultato dei casi precedenti?
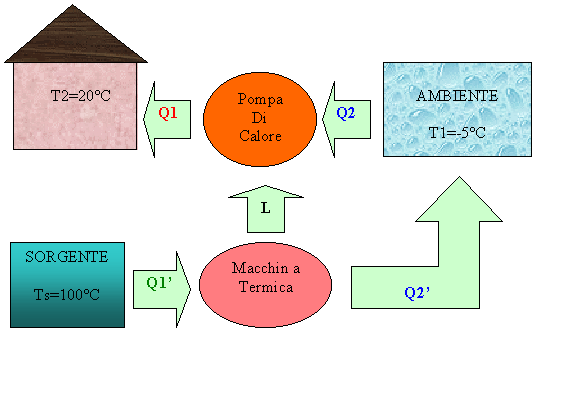
Si può calcolare il coefficiente economico della macchina termica introdotta in ultima ipotesi e si ottiene che:
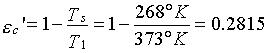
quindi
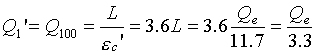
In questo caso il lavoro perduto, cioè la quantità di calore donata all’ambiente (serbatoio freddo) e quindi non convertita in lavoro utile è pari a
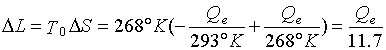
In conclusione, risulta quindi evidente come il metodo di riscaldamento mediante pompa di calore elettrica risulti più vantaggioso del metodo mediante resistenza elettrica, sia dal punto di vista economico(minor quantità di energia elettrica utilizzata) sia dal punto ambientale, in quanto si può considerare come effetto secondario del funzionamento di una pompa di calore quello di diminuire l’inquinamento termico dell’ambiente, prelevando calore da questo.
Si possono introdurre due grandezze che rendono conto in maniera sintetica delle conclusioni appena fatte:
COP(coefficient of performance) = energia utile / energia di funzionamento
CUC(coefficiente utilizzo combustibile) = energia usata / energia di partenza
Per i due metodi studiati si ottengono i seguenti valori :
1) COP = 1 CUC = 1
2) COP = 11.7 CUC = 1.5
Sapendo che, ad esempio, il COP assume sempre valori maggiori di 1, risulta evidente che i valori calcolati per queste due grandezze giustificano le conclusioni fatte in precedenza.
Fisica delle sostanze chimicamente pure
Una sostanza chimicamente pura (o sistema chimicamente omogeneo, volendo considerare la sostanza dal punto di vista termodinamico) ha la caratteristica di essere formata esclusivamente da molecole della stessa natura.
Ovviamente, sostanze di questo tipo possono assumere nell’ambiente che ci circonda ognuno dei tre possibili stati fisici della materia: solido, liquido, gassoso. Fornendo o prelevando calore al sistema omogeneo si può ottenere che questo passi di stato.
Possiamo notare, tuttavia, che esistono situazioni in cui una stessa sostanza, pura nel nostro caso, coesiste in due o persino tre stati differenti, come ad esempio solido e liquido, liquido e gas oppure solido liquido e gas.
Risulta a questo punto interessante poter sapere che comportamento hanno le variabili di stato pressione p e volume v del sistema omogeneo in corrispondenza di particolari temperature alle quali lo stesso si trova. Per poter far questo abbiamo a disposizione il diagramma delle isoterme in un sistema di riferimento (p, v), detto diagramma termodinamico (p,v).
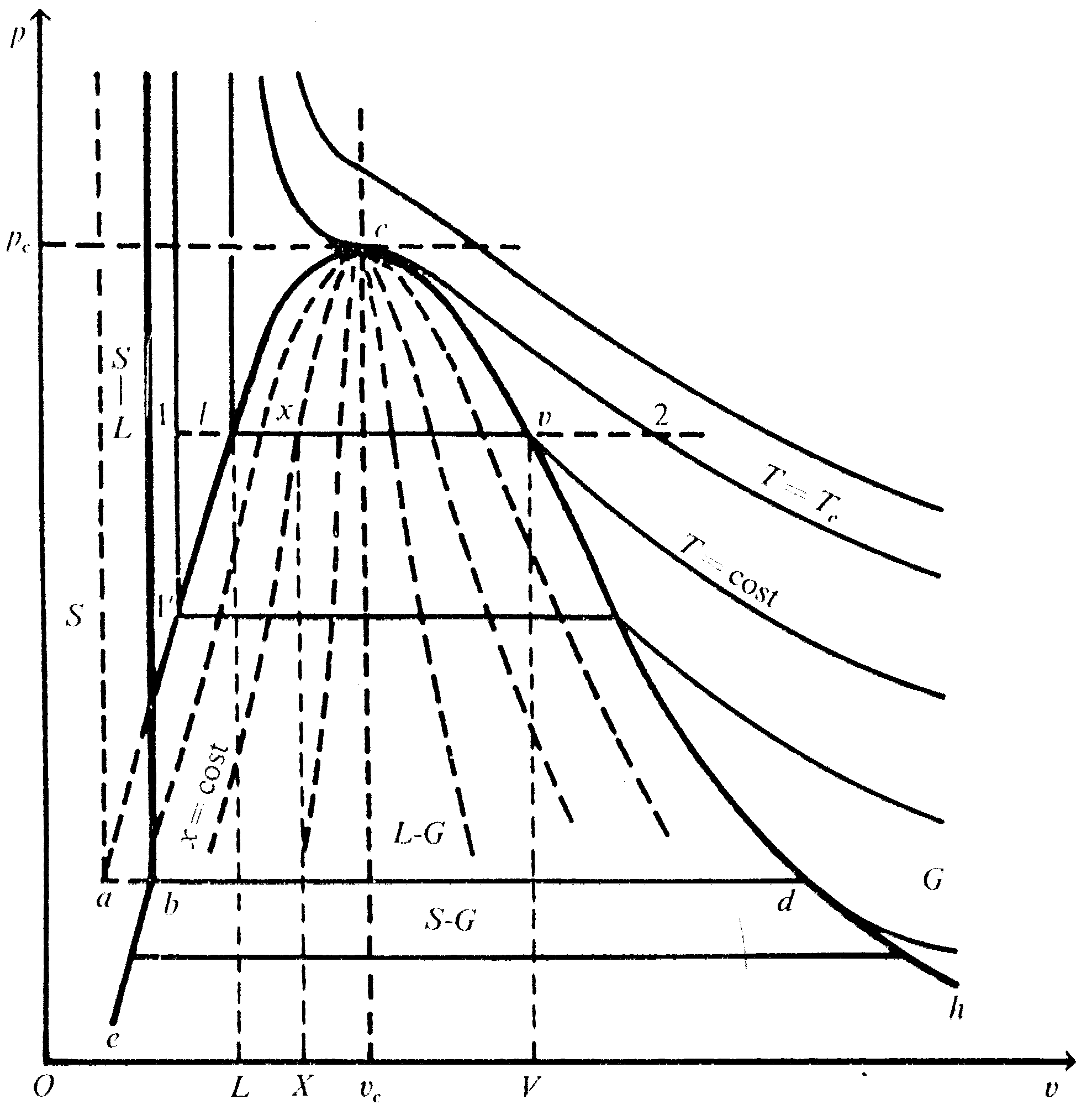
Fig. 1- Diagramma Termodinamico (p,v) dell’acqua che, solidificando, aumenta di
volume.
Questo diagramma può essere sostanzialmente suddiviso in 6 zone di interesse, (Fig. 1) che corrispondono a 6 diverse configurazioni fisiche della sostanza in esame. Identificando con Tc l’isoterma corrispondente alla cosiddetta temperatura critica (isoterma critica), si ha la seguente suddivisione:
Il punto c di intersezione tra l’isoterma critica e la curva di Andrews è detto punto critico, mentre il punto a è detto punto triplo. In questo punto, e quindi alla temperatura corrispondente all’isoterma che passa per esso, abbiamo la coesistenza di tutte e tre le fasi contemporaneamente: solido, liquido e gas. Per esempio, la temperatura del punto triplo di una sostanza comunemente utilizzata come l’acqua è pari a Tt = 0.01 °C , mentre la sua temperatura critica è pari a Tc = 374.15 °C.
In particolare, l’acqua è una sostanza pura che, contrariamente a quanto succede per la maggior parte delle sostanze di questa categoria, aumenta di volume nel passaggio dalla fase liquida a quella solida. Questo comportamento è ben illustrato dal diagramma (p,v) in Fig. 1. Si può notare infatti come in un intorno del punto triplo, lungo l’isoterma di confine tra solido-liquido e solido, ci sia un aumento di volume contraddistinto dal segmento a-b tratteggiato durante la comparsa della fase solida. Per la maggior parte delle sostanze, invece, in corrispondenza di questo intorno avviene esattamente il contrario; si ha cioè che al passaggio da solido a liquido corrisponde una diminuzione di volume.
Questo è la ragione per cui il ghiaccio galleggia in acqua liquida. Avendo, a parità di massa, volume maggiore, la fase solida riceve una spinta di Archimede positiva.
Da questi diagrammi possiamo vedere che, al variare delle tre variabili di stato (p,v,T) corrisponderà un cambiamento dell’aspetto esteriore e dello stato fisico della sostanza. Si può di conseguenza pensare di rappresentare in un riferimento cartesiano in tre dimensioni l’andamento di questi cambiamenti. Si assegna ad ognuno degli assi di riferimento una variabile di stato; unendo i punti ottenuti sperimentalmente per una sostanza pura, dato che le coordinate termodinamiche libere sono al più due, si ottiene una superficie, detta superficie (p,v,T), (Fig. 3) ad ogni punto della quale corrisponde uno stato d’equilibrio della sostanza ( o sistema).
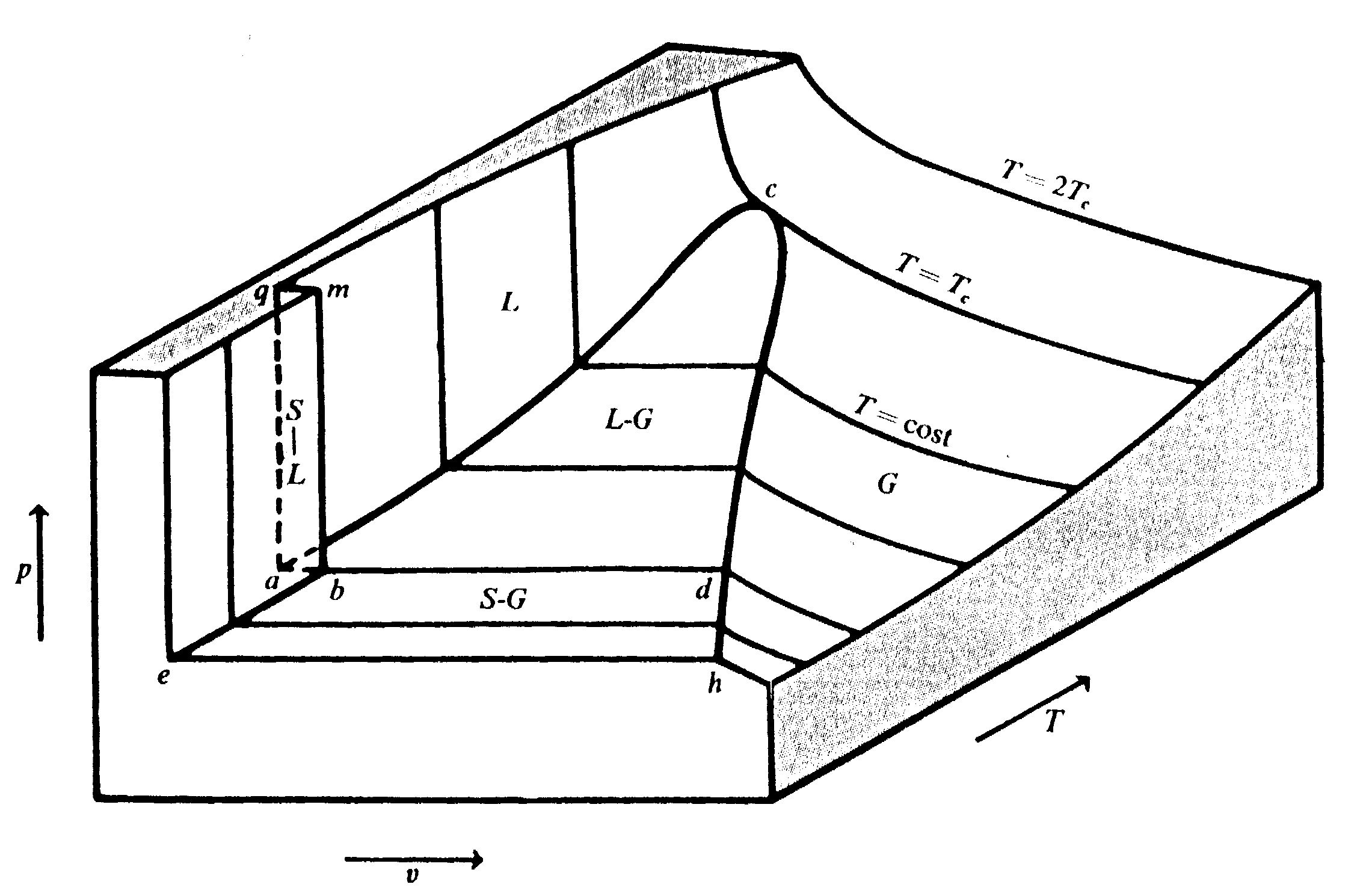
Fig. 3 - Superficie (p,v,T) di una sostanza che, solidificando, aumenta di volume
Questi sono diagrammi che danno informazioni solo sugli stati estremi di equilibrio di una trasformazione; dunque non servono a descrivere l’intero processo di trasformazione, che, per trasformazioni molto rapide, non passa per stati d’equilibrio.
Non è stato comunque possibile determinare un’unica equazione in grado di descrivere le superfici (p,v,T); quindi si è dovuto studiare il comportamento delle sostanze pure in particolari intervalli del dominio trattati separatamente. Le considerazioni che si possono fare in questi intervalli sono le seguenti:
![]() (1)
(1)
dove m indica la massa di una mole della sostanza considerata ed
![]() =8.314 J/°K mol viene detta costante universale.
=8.314 J/°K mol viene detta costante universale.
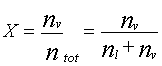 (2)
(2)
dove al numeratore ci sono le moli di vapore e al denominatore le moli totali di liquido e vapore della sostanza in un particolare punto sulla retta interpolatrice tra A e B. Come si può vedere, il titolo risulta quindi essere un numero puro che può variare nell’intervallo di valori [0..1]. Semplicemente, il titolo è un valore che ci restituisce, per ogni punto sulla retta interpolatrice, in che proporzione sono presenti la fase gassosa e quella liquida e quindi, quali sono le proprietà della sostanza nel punto stesso.
Ad esempio;
X = 0.3, significa che nel dato punto considerato, la sostanza è per il 30% in fase gassosa (0.3 moli di gas) e per il 70% in fase liquida (0.7 moli di liquido).
Qui di seguito si può vedere un esempio di tabella per vapori saturi:
Tabella 1. Acqua e vapore all’equilibrio ( ’ per liquido, ‘’ per vapore)
|
p(bar) |
t (°C) |
v’(mc/kg) |
v’’(mc/kg) |
h’(KJ/kg) |
h’’(KJ/Kg) |
s’(KJ/Kg) |
s’’(KJ/Kg) |
|
1,0 |
99.632 |
0.00104 |
1.694 |
417.51 |
2675.4 |
1.3027 |
7.3598 |
|
1.5 |
111.37 |
0.00105 |
1.159 |
467.13 |
2693.4 |
1.4336 |
7.2234 |
|
2.0 |
120.23 |
0.00106 |
0.8854 |
504.70 |
2706.3 |
1.5301 |
7.1268 |
A questo punto si pone il problema di voler calcolare, note due coordinate termodinamiche indipendenti, tutte le altre; vale a dire, determinare i valori di energia interna ( U), entalpia (H), entropia(S).
Le due coordinate termodinamiche che solitamente si scelgono per esprimere le alte funzioni di stato dei sistemi omogenei sono (p,v). Solamente nel caso specifico di una sostanza considerata nella zona di vapore saturo si scelgono (T,X), in quanto, se scegliessimo il volume sarebbe immediatamente nota la temperatura. Per interesse pratico, è utile andare a creare un modello di comportamento per i sistemi puri nella zona dei gas perfetti o ideali.
Il volume di un gas perfetto è facilmente determinabile dalla (1); ponendo
![]()
si vede che
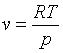
dove m indica la massa di una mole della sostanza in considerazione.
Abbiamo quindi le seguenti relazioni differenziali; dal I° Principio della termodinamica si ottiene che:
![]() (3)
(3)
dove
![]()
mentre
![]() (4)
(4)
dove
![]()
Dal teorema di Joule possiamo affermare che Cp, Cv dipendono solamente dalla temperatura T, cioè
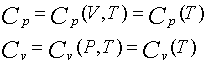
di conseguenza, integrando in (3) e (4) si ottiene
![]() (5)
(5)
![]() (6)
(6)
Siccome u, h sono grandezze riferite a meno di una costante, si fissano come valori di riferimento per queste due grandezze
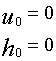 riferite alla temperatura
riferite alla temperatura ![]()
di conseguenza si può notare che vale la relazione:
![]()
che, per come è stata definita, ha validità generale.
Allo stesso modo si possono derivare le relazioni fondamentali che determinano l’ultima coordinata termodinamica rimasta da studiare, l’entropia s.
Procedendo parallelamente , dalle espressioni del I° principio mediante u e h abbiamo:
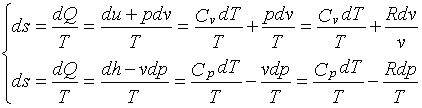 (8)
(8)
poiché possiamo vedere dall’equazione di stato dei gas perfetti che valgono le seguenti relazioni
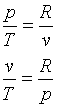
A questo punto, integrando in (7) si ottiene che
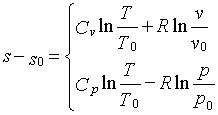 (8)
(8)
note rispettivamente (v,T) oppure (p,v), prendendo come riferimento per l’entropia il valore
![]() quando
quando ![]()