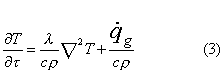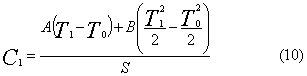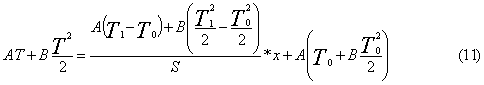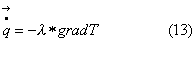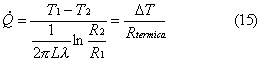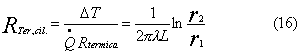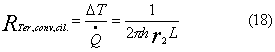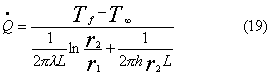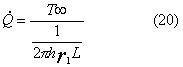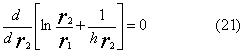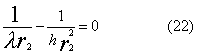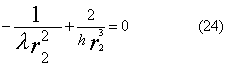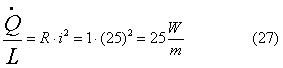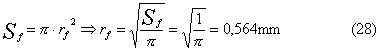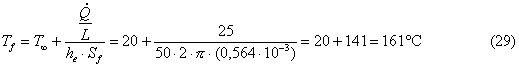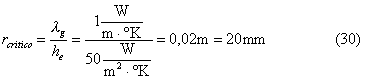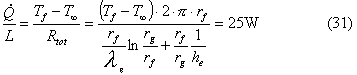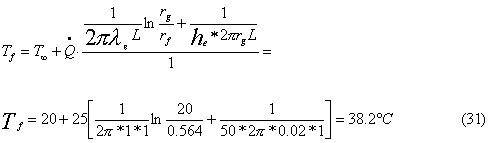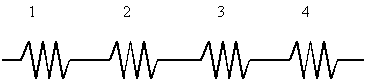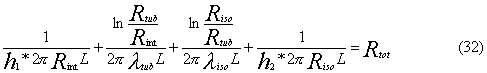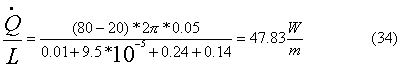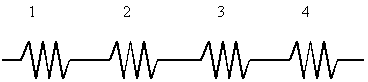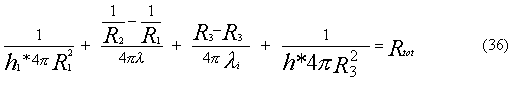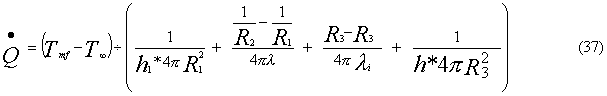Indice
1. Scambio termico
1.1. Conducibilità
termica l
1.2. Conduttore elettrico percorso da corrente
2.
Esercizi sullo scambio termico
2.1. Raggio critico di un isolante
2.2. Tubo percorso da liquido o gas
2.3. Sfera cava isolata
2.4. Tabelle
conducibilità termica
SCAMBIO TERMICO
1.1. Conducibilità termica l
Quando due corpi a
temperature differenti si trovano a contatto, si verifica una trasmissione di
calore dal corpo più caldo a quello più freddo, in altre parole si ha quello
che è stato definito uno scambio termico per conduzione.
Questo
fenomeno è già stato descritto per mezzo della legge di Fourier:
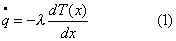
dove
la conducibilità termica l (W/mK) è la grandezza caratteristica del materiale che viene generalmente
considerata costante per consentire la semplificazione dei calcoli in cui
compare.
Questa
imprecisione è ovviamente trascurabile, poiché la soluzione di problemi
riguardanti lo scambio termico comportano sempre una certa approssimazione
dovuta all'effettiva difficoltà di descrivere esaurientemente il fenomeno
fisico con modelli matematici. Maggiormente l'errore è trascurabile
considerando l'andamento pressoché lineare della variabile; l è tuttavia funzione della temperatura:
l=l(T) (2)
Se risulta necessario
eseguire calcoli più accurati, la conducibilità termica non può più essere
considerata costane, la grandezza l deve quindi essere integrata (nell'Equazione di Fourier (3) l = cost era stata portata fuori dal laplaciano).
Consideriamo
per semplicità il comportamento in un caso mono dimensionale di una lastra la
cui temperatura varia tra T1 e T0, prima per l = cost:
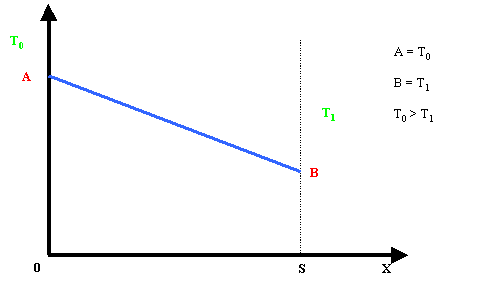
Fig.1 – Andamento lineare di l = cost.
Poi
per l = l(T):
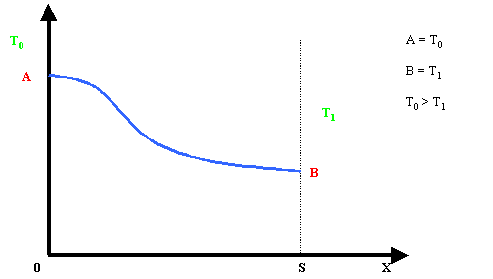
Fig.2 - Andamento curvilineo di l=l(T).
Come
emerge dal grafico l'approssimazione lineare comporta una perdita
d'informazione.
Analizziamo
il secondo caso utilizzando l'Equazione
di Fourier:
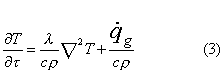
Imponiamo
le condizioni iniziali:
- qg=0 perché non c'è generazione
- regime
stazionario: derivata rispetto al tempo nulla
L'equazione
(3) diventa:
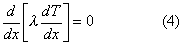
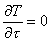
(essendo per la
condizione di stazionarietà)
Imponiamo l in funzione della temperatura:
l = A + BT (5)
poi sostituiamo nella
(4):
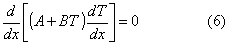
Adesso possiamo separare
le variabili:
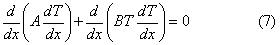
e portare fuori A e B;
integrando una prima volta si ottiene:
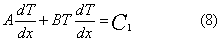
Integrando una seconda
volta:
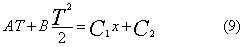
Otteniamo quindi una
parabola.
Studiamo
per semplicità le condizioni al contrario (ovvero in funzione di x anziché di
T); osserviamo che imponendo la prima condizione si ottiene:
x = 0 Þ T = T0 allora C2 = AT0 + BT20/2
imponendo, invece, la seconda:
x = S Þ T = T1 allora AT1 + BT21/2
= C1S + AT0 + BT20/2
quindi ricaviamo C1:
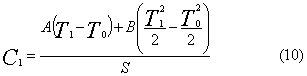
Infine sostituendo nella
(9) C1 e C2:
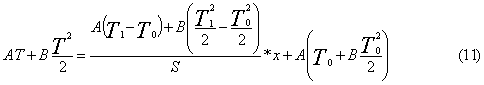
Poiché
x varia con il quadrato di T e non
viceversa, la parabola assume la seguente forma, con il verso positivo
orientato in senso contrario all'asse x (T0>T1):
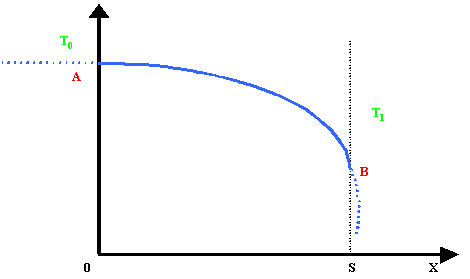
Fig.3 - Parabola orientata lungo -x.
La
concavità della parabola rivolta verso l'alto indica il comportamento di l al variare della temperatura:
- B > 0 Þ la crescita della temperatura fa aumentare la conducibilità termica
- B < 0 Þ la temperatura in diminuzione fa aumentare la conducibilità termica
Se
si elimina il termine costante C2 dalla (9) si ottiene:
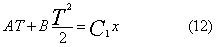
Per
semplicità consideriamo il caso T0
< T1; al crescere
di T la curva continua a crescere
(nella fig. 4 la curva tratteggiata).
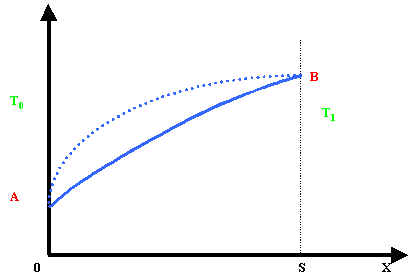
Fig.4 - Andamento di l al crescere della temperatura.
Consideriamo
la legge di Fourier generalizzata, applicata cioè ad un vettore nello spazio:
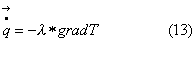
Poiché
il calore scambiato è costante, anche il prodotto -l*gradT è costante.
Perciò,
nei materiali normalmente, la concavità della parabola è sempre rivolta verso
l'alto; infatti, il valore di l è piuttosto piccolo e quindi di conseguenza
aumenta il gradiente di T.
Prendiamo,
ad esempio, il rivestimento di una caldaia (Fig.5) e osserviamo il
comportamento della conducibilità termica l nei diversi strati di materiali che formano la struttura.
Se
l è costante per calcolare lo scambio termico attraverso lo strato isolante
della parete della caldaia è sufficiente considerare la serie delle resistenze
equivalenti:
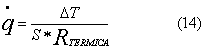
Poiché
l non è costante troviamo al centro della parete
temperature molto maggiori di quanto previsto; questo comporta una notevole
sollecitazione dell'isolante che si trova a contatto con temperature molto
elevate frutto del forte gradiente di T,
causato dalla grande differenza di temperatura tra la parete interna e quella
esterna della caldaia.
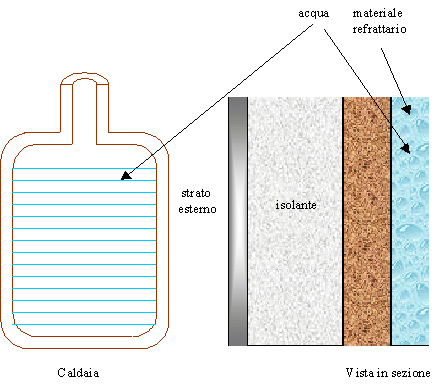
Fig.5 - Parete isolante della caldaia.
NOTA
Le tabelle riportano dati sulla variabilità di l solo per alcune temperature prefissate, perciò se non si conoscono i
coefficienti A e B della formula (5) risulta inevitabile considerare l costante anziché funzione della temperatura.
È quindi indispensabile prevedere un adeguato fattore di sicurezza nella
progettazione di impianti di questo tipo.
1.2. Conduttore
elettrico percorso da corrente
Consideriamo
un conduttore elettrico percorso da corrente e rivestito da una guaina di
materiale isolante.
Lo
strato interno è un materiale di tipo metallico ad elevato potere conduttivo
(ad esempio Cu, Al, ecc.), lo strato esterno una guaina di materiale plastico
isolante, adatto sia a dissipare il calore, sia a proteggere da un eventuale
contatto con il filo.
In
Fig. 6 è riportato un esempio di conduttore rame pieno:
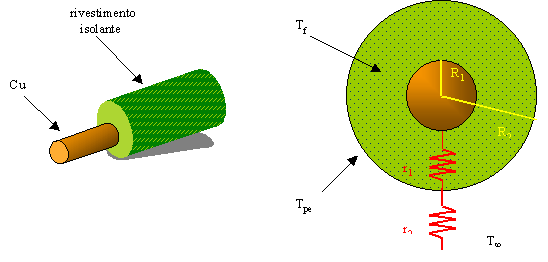
Fig.6 - Isometria cilindrica conduttore elettrico.
Dentro
al rame la T non è uniforme poiché
si ha generazione di calore per effetto Joule, ma l'elevata conducibilità del
materiale contribuisce a livellare i dislivelli di temperatura.
Il
calore interno prodotto va comunque dissipato, poiché per quanto piccolo (è dell'ordine
di 1/1000) è sufficiente a produrre un incremento di temperatura dannoso per le
apparecchiature.
Per
calcolare la potenza dispersa da un conduttore di lunghezza L, consideriamo la serie delle
resistenze termiche equivalenti (Fig.7):
r1 = resistenza
di conduzione del materiale isolante
r2 =
resistenza di convezione dell'aria esterna all'isolante
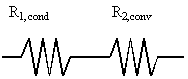
Fig.7 - Rappresentazione mediante l'uso delle resistenze.
Per
lo strato conduttivo ricordiamo l'espressione della potenza termica scambiata
da uno strato cilindrico
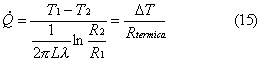
Quindi
otteniamo la resistenza termica di uno strato cilindrico:
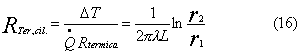
Mentre
la potenza termica scambiata per convezione:
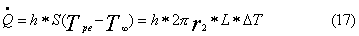
E la resistenza termica relativa è uguale a:
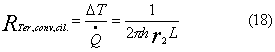
Sommando
le due resistenze termiche equivalenti otteniamo la potenza termica dissipata
attraverso il rivestimento:
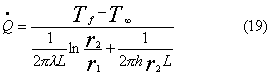
Dove h, l, Tf,
T¥ sono rispettivamente il coefficiente di
convezione all’esterno dell'isolante, la conducibilità termica della guaina
isolante, la temperatura all'interno dell'isolante e la temperatura all'esterno
dell'isolante.
La
potenza termica dissipata attraverso il rivestimento isolante è funzione del
raggio della guaina stessa; è interessante notare come la funzione abbia un
massimo in prossimità del raggio critico Rc
(Fig.8).
Al
crescere del raggio r2 della guaina prima si ha un aumento della
potenza termica dissipata, poi raggiunto il raggio critico inizia a diminuire.
Il fenomeno è causato dalla diminuzione della resistenza convettiva.
Finché
il raggio r2 è piccolo si ha un aumento della superficie dissipativa
rispetto al filo nudo, quindi cresce lo scambio termico e diminuisce la
temperatura del filo; poi al crescere del raggio il termine a denominatore
cresce troppo e aumenta la resistenza termica.
Se
non ci fosse la guaina:
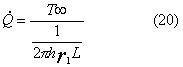

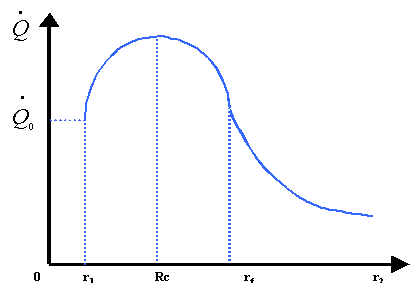
Fig.8 - Raggio critico isolante
NOTA
Tanto maggiore è la resistenza termica del materiale isolante e tanto
maggiore va il rivestimento del filo conduttore.
Infatti, quando c'è un corto circuito, si ha un principio di
surriscaldamento del filo, la guaina isolante inizia a sciogliersi rendendo il
processo irreversibile, poiché la capacità dissipativi del rivestimento
diminuisce progressivamente fino alla fusione completa del conduttore.
Rc è il raggio ottimale: ricaviamo il suo valore effettivo trovando il
massimo nell'equazione (19). Deriviamo il denominatore rispetto a r2 e uguagliamo a 0:
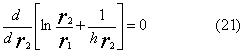
(la costante 1/(2pL) si può eliminare)
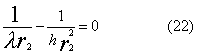
Poiché
r2 > r1 ¹ 0 dalla (22) otteniamo il raggio critico:

Se
ci fosse anche la componente dell'irraggiamento al posto do h useremmo il coefficiente convettivo
totale htot.
Quando il raggio della
guaina supera il raggio ottimale si ha un'inversione di tendenza e il
contributo dissipativo della maggior superficie è superato dal contributo
negativo della guaina isolante. Se, ad esempio, il rivestimento esterno ricopre
un tubo dell'acqua calda il suo contributo non deve più essere dissipativo, ma
bensì isolante: il raggio deve quindi essere per lo meno superiore al punto di
flesso del grafico.
Per
trovare il flesso è sufficiente annullare la derivata seconda:
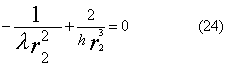
Il
raggio di flesso è perciò:

Quindi
il raggio di flesso (minimo comportamento isolante) è il doppio del raggio
critico (massimo comportamento isolante). Per questo motivo il raggio critico
di molti isolanti per tubi dell'acqua è inferiore al raggio del tubo metallico
in cui scorre il liquido.
ESERCIZI SULLO SCAMBIO TERMICO
2.1. Raggio
critico di un isolante
Sia dato un filo
elettrico (Fig.9) di sezione S pari a 1mm2 con una resistenza R, per
unità di lunghezza, pari a 1W/m. Il filo è percorso da una corrente i pari a 5A (è un conduttore di
bassa qualità).
Determinare la
temperatura del filo, conoscendo il valore del coefficiente di convezione
esterno he pari a 50W/m2°K.
Tale valore è volutamente elevato in quanto comprende anche la componente dello
scambio termico per irraggiamento.
Determinare infine la
potenza dispersa per metro di lunghezza:
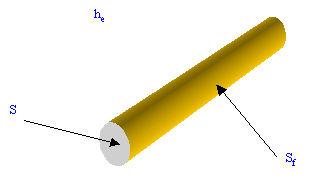
Fig.9 - Filo elettrico.
Soluzione:
La
potenza dispersa per la componente convettiva è uguale a:
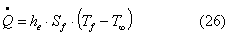
Dove Sf è la superficie esterna del filo, Tf è la temperatura del filo
e T¥ = 20°C.
La
potenza termica dispersa per effetto Joule per unità di lunghezza è uguale a:
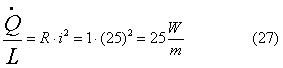
Considerando
che il filo ha una sezione S pari a 1mm2, il suo raggio rf
si calcola nel seguente modo:
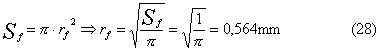
Possiamo
quindi ricavare la temperatura del filo:
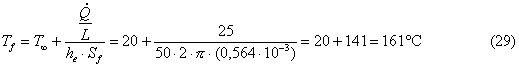
E'
una temperatura pericolosa, il filo nudo andrà necessariamente ricoperto
con un isolante adeguato per evitare che si bruci.
Il
raggio ottimale della guaina isolante sarà il raggio critico.
Supponiamo
di utilizzare un materiale come la gomma con una conducibilità termica lg pari a 1W/m°K, allora il raggio ottimale sarà:
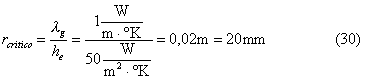
Lo spessore della guaina
è chiaramente esagerato rispetto al diametro del filo poiché la conducibilità
termica è troppo elevata..
La
nuova potenza scambiata varrà:
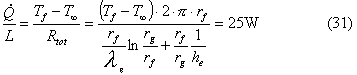
E
la nuova temperatura del conduttore sarà:
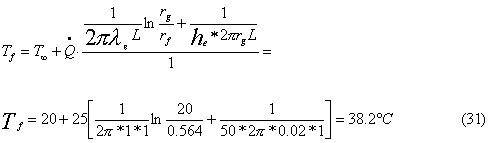
La
temperatura del conduttore con il nuovo strato d'isolante è accettabile.
2.2. Tubo
percorso da liquido o gas
Si consideri un tubo
vuoto percorso da un liquido o da un gas rivestito con materiale isolante
(fig.10). Il condotto è composto da uno strato cilindrico doppio nel quale la
superficie interna è normalmente realizzata con un materiale piuttosto
conduttivo per il calore, in quanto metallico, mentre intorno generalmente si
utilizza un materiale che impedisca la dispersione del calore.
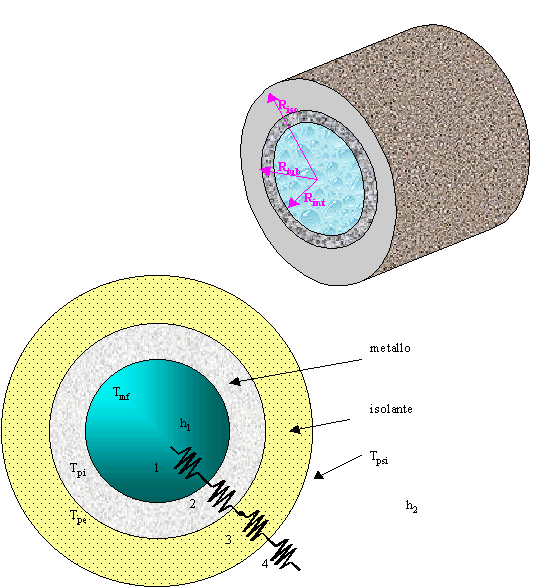 Fig.10 - Tubo con acqua.
Fig.10 - Tubo con acqua.
La resistenza interna lega la temperatura media del fluido a quella di
parete del tubo all'interno.
Poiché
il tubo è di metallo (un ottimo conduttore termico) la differenza di
temperatura fra le due pareti esterna ed interna è trascurabile: Tpe » Tpi.
Dati:
Temperatura media del
fluido: Tmf
= 80°C
Temperatura dell'aria: T¥ = 20°C
Raggio interno del tubo: Rint
= 0.05m
Raggio esterno del tubo: Rtub
= 0.055m
Raggio dell'isolante: Riso
= 0.07m
Coefficiente di
convezione del fluido: h1
= 100 W/m2K
Coefficiente di
convezione dell'aria: h2
= 5 W/m2K
Conducibilità termica del
tubo: ltub = 50W/mK
Conducibilità termica
dell'isolante: liso = 0.05W/mK
Soluzione:
Utilizziamo
il metodo delle resistenze equivalenti (Fig.11):
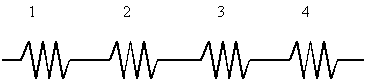
Fig.11 - Rappresentazione mediante l'uso delle resistenze.
Sommando
i singoli contributi si ottiene:
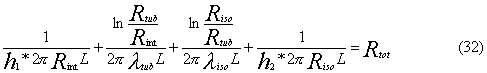
La
potenza complessiva scambiata vale:
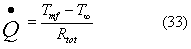
E
quindi la potenza scambiata per unità di lunghezza risulta uguale a:
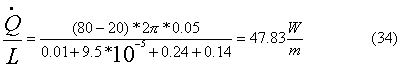
Dai calcoli risulta
evidente che la resistenza del metallo è del tutto trascurabile (il materiale è
un ottimo conduttore e offre una resistenza molto piccola), mentre il termine
convettivo del liquido interno era quasi trascurabile. Il coefficiente di
convezione del fluido è ovviamente molto elevato, ma non abbastanza da far
trascurare la resistenza interna senza commettere una piccola imprecisione.
Nel caso di due fluidi a
contatto (ad esempio aria-aria), il termine sarebbe invece essenziale per
ottenere un risultato corretto.
2.3. Sfera cava isolata
Consideriamo una sfera cava di raggio interno R1
e di raggio esterno R2, avvolta in uno strato esterno isolante: ad
esempio un'autoclave.
Supponiamo che la temperatura della superficie
sferica interna sia Tmf e quella
della superficie sferica esterna del materiale isolante sia T¥.
Nell'interno del contenitore metallico è contenuto
un fluido alla temperatura media Tmf
(Fig.12). Trovare la potenza termica complessiva scambiata.
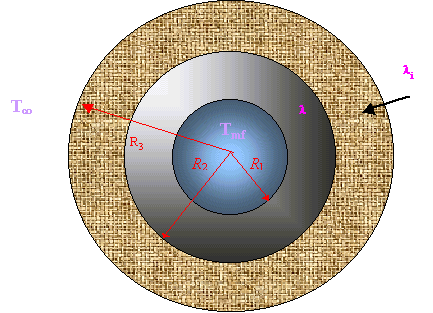
Fig.12
- Strato sferico con
isolante.
Dati:
Temperatura media del
fluido: Tmf
Temperatura dell'aria: T¥
Raggio interno della
sfera metallica: R1
Raggio esterno della
sfera metallica: R2
Raggio dell'isolante: R3
Coefficiente di
convezione del fluido: h1
Coefficiente di
convezione dell'aria: h2
Conducibilità termica
della sfera metallica: l
Conducibilità termica
dell'isolante: li
Soluzione:
In regime stazionario la potenza termica è uguale
a:
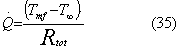
Per trovare la potenza termica complessiva
scambiata dalla sfera isolata (35), utilizziamo il metodo delle resistenze
equivalenti (Fig.13):
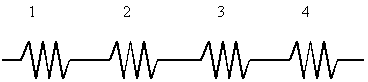
Fig.13 - Rappresentazione mediante l'uso delle resistenze.
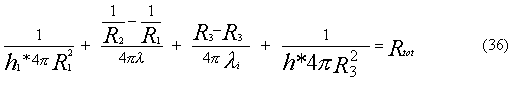
Quindi dalla (35) si ottiene la potenza termica
cercata:
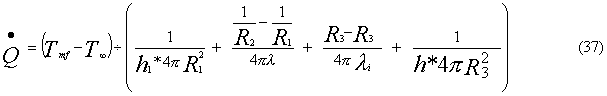
2.4. Tabelle
conducibilità termica
|
Materiale
|
Temperatura (°C)
|
Conducibilità termica l (W/mK)
|
|
Metalli
|
|
|
|
Acciaio
|
20
|
52
|
|
Alluminio
|
20
|
220
|
|
Argento
|
20
|
420
|
|
Oro
|
40
|
296
|
|
Piombo
|
20
|
35
|
|
Platino
|
20
|
70
|
|
Rame
|
20
|
380
|
|
Metalli liquidi
|
|
|
|
Mercurio
|
10
|
8
|
|
Piombo
|
500
|
15
|
|
Potassio
|
500
|
37
|
|
Sodio
|
500
|
66
|
|
Non metalli
|
|
|
|
Amianto fuso
|
0
|
0.15
|
|
Asfalto
|
20
|
0.70
|
|
Cotone
|
30
|
0.04
|
|
Ghiaccio
|
0
|
2.2
|
|
Lana di vetro
|
0
|
0.035
|
|
Polistirolo espanso
|
0
|
0.032
|
|
Poliuretano espanso
|
0
|
0.021
|
|
Vetro
|
15
|
0.73
|
|
Sughero in lastre
|
0
|
0.04
|
|
Liquidi
|
|
|
|
Acqua
|
0
|
0.57
|
|
Acqua
|
50
|
0.64
|
|
Acqua
|
100
|
0.67
|
|
Ammoniaca
|
0
|
0.54
|
|
Glicerina
|
20
|
0.28
|
|
Gas ( p = 1 bar)
|
|
|
|
Aria
|
0
|
0.024
|
|
Aria
|
100
|
0.031
|
|
Azoto
|
0
|
0.024
|
|
Idrogeno
|
0
|
0.16
|
|
Ossigeno
|
0
|
0.025
|
|
Vapor d'acqua saturo
|
200
|
0.034
|
|
Materiale
|
Temperatura (°C)
|
Conducibilità termica l (W/mK)
|
|
Miscellanea
|
|
|
|
Acido formico
|
20
|
0.180
|
|
Glicerina
|
20
|
0.195
|
|
Toluene
|
20
|
0.16
|
|
Acido nitrico
|
20
|
0.28
|
|
Acetone
|
20
|
0.176
|
|
Coke
|
400
|
0.095
|
|
Vetro (pyrex)
|
193
|
1.0
|