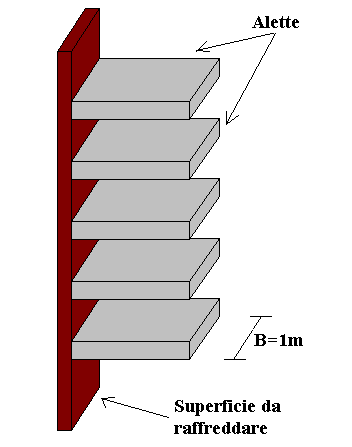
Superfici Alettate
Le superfici alettate sono utilizzate per aumentare lo scambio termico in modo poco costoso quando in un sistema complesso c’è un anello debole come la convezione naturale in aria. In particolare vengono impiegate per raffreddare dispositivi elettronici quali transistori di potenza, microprocessori, televisori.

Fig.1 – Vista di Superfici Alettate nello Spazio.
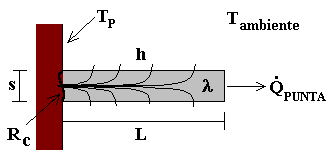
Fig.2 – Singola Aletta in Sezione.
Nella trattazione seguente considereremo solo alette con sezione rettangolare poiché risultano più facili da studiare, ma ricordiamo che ne esistono anche altre di forma diversa ed a volte più efficaci che presentano però un’analisi difficile (vengono studiate per via numerica).
Nel nostro studio facciamo le seguenti ipotesi semplificative:
Studio della temperatura su una aletta singola di sezione rettangolare
Vediamo allora di studiare la variazione di temperatura e la variazione di flusso scambiato al variare della distanza dalla superficie di contatto di una singola aletta. Nella seguente figura, fig. 3, riportiamo in ordinata la temperatura T(x) dell’aletta ed in ascissa la distanza x dalla superficie da raffreddare. Ovviamente si ha un abbassamento della temperatura a partire da TP (temperatura di parete) fino ad arrivare progressivamente a T![]() (temperatura dell’ambiente circostante).
(temperatura dell’ambiente circostante).
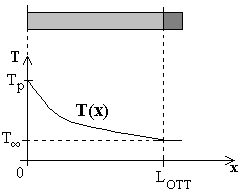
Fig.3 – Andamento della Temperatura in funzione della Distanza.
La distanza x in corrispondenza della quale la temperatura raggiunge un valore pari a T![]() è la lunghezza ottimale L. Non è conveniente usare alette più lunghe di L poiché fanno da freno al moto dell’aria.
è la lunghezza ottimale L. Non è conveniente usare alette più lunghe di L poiché fanno da freno al moto dell’aria.
In realtà il grafico della temperatura non parte da TP ma da un valore inferiore a causa della presenza della resistenza di contatto Rc.
Anche la densità di flusso termico scambiato è più grande vicino alla superficie di contatto e diminuisce allontanandoci da questa.
Per studiare il fenomeno, visto che non conosciamo a priori come varia la temperatura in funzione della distanza, consideriamo un tratto infinitesimale lungo dx. La situazione si presenta in questo modo:
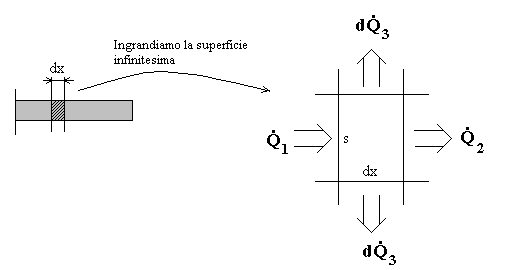
Fig.4 – Scambio Termico su un Tratto Infinitesimo.
![]() : potenza termica che entra per conduzione.
: potenza termica che entra per conduzione.
![]() : potenze termica che esce per conduzione.
: potenze termica che esce per conduzione.
![]() : potenza termica che esce per convezione in aria (scriviamo
: potenza termica che esce per convezione in aria (scriviamo ![]() e non semplicemente
e non semplicemente ![]() poiché tale potenza si riferisce ad una superficie infinitesima di lato dx).
poiché tale potenza si riferisce ad una superficie infinitesima di lato dx).
s: spessore
dx : lunghezza del tratto infinitesimo
A regime il calore in entrata deve essere uguale a quello in uscita :
![]() (1)
(1)
Utilizziamo ora la legge di Fourier per esprimere il calore in corrispondenza delle distanze x e x+dx :
![]() e
e ![]() (2)
(2)
l
è la conducibilità del materiale di cui è fatta l’aletta.
La seconda delle (2) è stata ottenuta attraverso lo sviluppo in serie di Taylor arrestato al I ordine della funzione q(x). I flussi di calore ![]() si trovano moltiplicando q(x) per la superficie
si trovano moltiplicando q(x) per la superficie ![]() . Per semplificare i calcoli abbiamo preso B=1m, quindi nelle formule successive non faremo comparire la dimensione B ricordando di inserire le unità di misura corrette di volta in volta.
. Per semplificare i calcoli abbiamo preso B=1m, quindi nelle formule successive non faremo comparire la dimensione B ricordando di inserire le unità di misura corrette di volta in volta.
![]() (3)
(3)
Ora andiamo a riscrivere il bilancio (1) inserendo i valori trovati attraverso le relazioni (2) e (3) di ![]() e
e ![]() :
:
![]() (4)
(4)
Il calore ![]() deriva da un puro scambio termico convettivo:
deriva da un puro scambio termico convettivo:
![]() (5)
(5)
h è il coefficiente di convezione.
Sostituendo ora il valore dell’espressione (5) nell’equazione (4) otteniamo :
![]() (6)
(6)
Il termine dx compare in entrambi i membri quindi possiamo toglierlo e riscrivere la (6) nel seguente modo :
![]() (7)
(7)
La (7) è un’equazione differenziale a variabili separabili di II grado.
Facciamo ora le seguenti posizioni :
e riscriviamo la (7) nella nuova funzione variabile q :
![]() (8)
(8)
L’equazione (8) ha la stessa forma dell’equazione di Helmots trovata per le onde acustiche quindi presenta la stessa soluzione generale :
![]() (9)
(9)
In questo caso, m2 è un coefficiente per costruzione sempre maggiore di 0 , quindi la sua radice quadrata è ancora positiva e di conseguenza la soluzione è la somma di due funzioni esponenziali non oscillanti.
(Ricordiamo che nel caso delle onde acustiche il coefficiente m2 è negativo ed m è un numero immaginario quindi la soluzione è pari alla somma di due funzioni esponenziali smorzate oscillanti).
Per trovare le soluzioni particolari imponiamo le due condizioni al contorno in x=0 ed in x=L.
se non considerassimo la resistenza di contatto Rc avremmo :
![]()
ma tenendo conto anche della Rc otteniamo :
![]() (10)
(10)
![]()
![]() (11)
(11)
Dalle condizioni (10) e (11) otteniamo un sistema di due equazioni e due incognite che ci permette di trovare le costanti A e B indicate nella soluzione generale (9). Omettendo i passaggi intermedi scriviamo direttamente le espressioni di A e B :
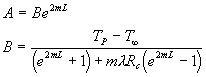 (12)
(12)
Inserendo la soluzione trovata di q e la sua derivata seconda nell’espressione di partenza (8), si arriva alla seguente formula finale :
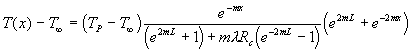 (13)
(13)
la quale ci permette di trovare la temperatura in funzione della distanza dalla superficie di contatto.
Tale formula si trova sui libri ma nella pratica non la si usa poiché più che analizzare la temperatura su tutta la superficie, serve sapere la variazione di scambio termico che si ottiene inserendo l’aletta rispetto alla situazione iniziale quando l’aletta non è ancora stata aggiunta.
Guadagno prodotto da una singola aletta
Definiamo il seguente rapporto :
![]() : Guadagno Prodotto dall’Aletta
: Guadagno Prodotto dall’Aletta
![]() : flusso termico ottenuto con l’aletta
: flusso termico ottenuto con l’aletta
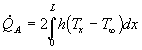 e svolgendo l’integrale si arriva a :
e svolgendo l’integrale si arriva a :
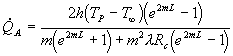 (14)
(14)
![]() : flusso termico ottenuto senza aletta
: flusso termico ottenuto senza aletta
![]() (15)
(15)
Svolgendo il rapporto tra la (14) e la (15) e semplificando l’espressione trovata si arriva alla seguente relazione :
![]() sempre (16)
sempre (16)
G è dunque l’incremento di scambio termico sulla porzione di spazio occupata dall’aletta.
Efficienza di una singola aletta
Definiamo un altro rapporto :
![]() : Efficienza dell’aletta
: Efficienza dell’aletta
![]() è lo stesso flusso termico definito sopra e
è lo stesso flusso termico definito sopra e ![]() la potenza termica che si otterrebbe se tutta l’aletta fosse alla stessa temperatura di parete TP (aletta che non perde temperatura).
la potenza termica che si otterrebbe se tutta l’aletta fosse alla stessa temperatura di parete TP (aletta che non perde temperatura).
![]() (17)
(17)
Tale valore è anche quel valore di ![]() che fornisce il massimo valore del guadagno GMAX.
che fornisce il massimo valore del guadagno GMAX.
Facendo allora il rapporto tra la (14) e la (17) si ottiene :
![]() (18)
(18)
Si può anche esprimere il guadagno in funzione dell’efficienza :
![]() (19)
(19)
Leggendo l’espressione (19) si vede che conviene utilizzare alette lunghe e sottili, ma diminuendo troppo il loro spessore, l’efficienza eA assume valori molto piccoli e di conseguenza si abbassa anche il guadagno G (l’efficienza è al numeratore, mentre lo spessore è al denominatore).
Caso limite : "ALETTA TOZZA"
Prendiamo il caso particolare di un’aletta avente lunghezza L pari al suo spessore s (figura 5).
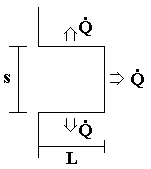
Fig.5 – Aletta Tozza avente L=s.
Dalla formula (19), essendo L=s, e supponendo di avere un’aletta senza perdite di temperatura con efficienza eA=1, si ottiene un guadagno G pari a 2. Analizzando però la figura 5 e sommando i contributi delle tre superfici dell’aletta a contatto con l’aria si dovrebbe ottenere un guadagno G pari a 3. Tale differenza di risultati è dovuta al fatto che utilizzando la formula (19), abbiamo implicitamente trascurato il calore scambiato dalla punta ![]() .
.
Per far comparire il contributo del calore ![]() sostituiamo ad L la nuova lunghezza
sostituiamo ad L la nuova lunghezza ![]() in tutte le relazioni precedentemente trovate. In particolare il guadagno G diventa:
in tutte le relazioni precedentemente trovate. In particolare il guadagno G diventa:
![]() (20)
(20)
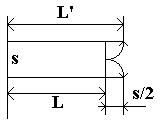
Fig.6 – Metodo Grafico per ottenere L’.
Contributo di una Serie di Alette
Fino ad ora abbiamo analizzato il contributo dovuto ad una sola aletta, ora invece cerchiamo delle relazioni (in particolare del guadagno GTOT e dell’efficienza eTOT) che tengano conto del contributo totale di un certo numero di alette montate su una superficie (figura 7).
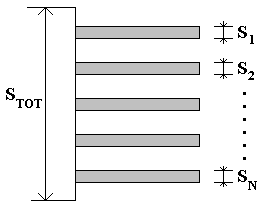
Fig.7 – Superficie con N alette
N : numero di alette applicate
STOT : superficie totale senza alette
S1, S2, …, SN : superficie di ogni aletta
La potenza scambiata totale ![]() si può esprimere come somma di due contributi (quello dovuto alla superficie libera e quello dovuto alla superficie occupata dalle alette):
si può esprimere come somma di due contributi (quello dovuto alla superficie libera e quello dovuto alla superficie occupata dalle alette):
![]() (21)
(21)
dove :![]() è la superficie occupata dalle alette.
è la superficie occupata dalle alette.
(STOT-SAL) è la superficie ove non sono applicate le alette.
![]() :normale convezione in aria
:normale convezione in aria
Per trovare qal ricorriamo alla definizione del guadagno G data precedentemente
![]()
![]() (non compare la superficie poiché essendo sia al numeratore che al denominatore si può semplificare)
(non compare la superficie poiché essendo sia al numeratore che al denominatore si può semplificare)
quindi
![]() .
.
Sostituendo a G l’espressione (20) si trova :
![]() (22)
(22)
e tornando all’espressione (21) della potenza scambiata totale :
![]() (23)
(23)
Da qui posso trovare il guadagno GTOT e l’efficienza eTOT :
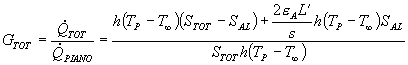 (24)
(24)
![]() è la potenza termica in assenza di alette
è la potenza termica in assenza di alette
![]() (25)
(25)
![]() è la potenza se tutte le alette fossero senza perdita di temperatura (eA=1).
è la potenza se tutte le alette fossero senza perdita di temperatura (eA=1).
Alette di sezione diversa da quella rettangolare
Nelle seguenti figure sono illustrati i grafici che ci forniscono l’efficienza eA di alette di forma diversa.
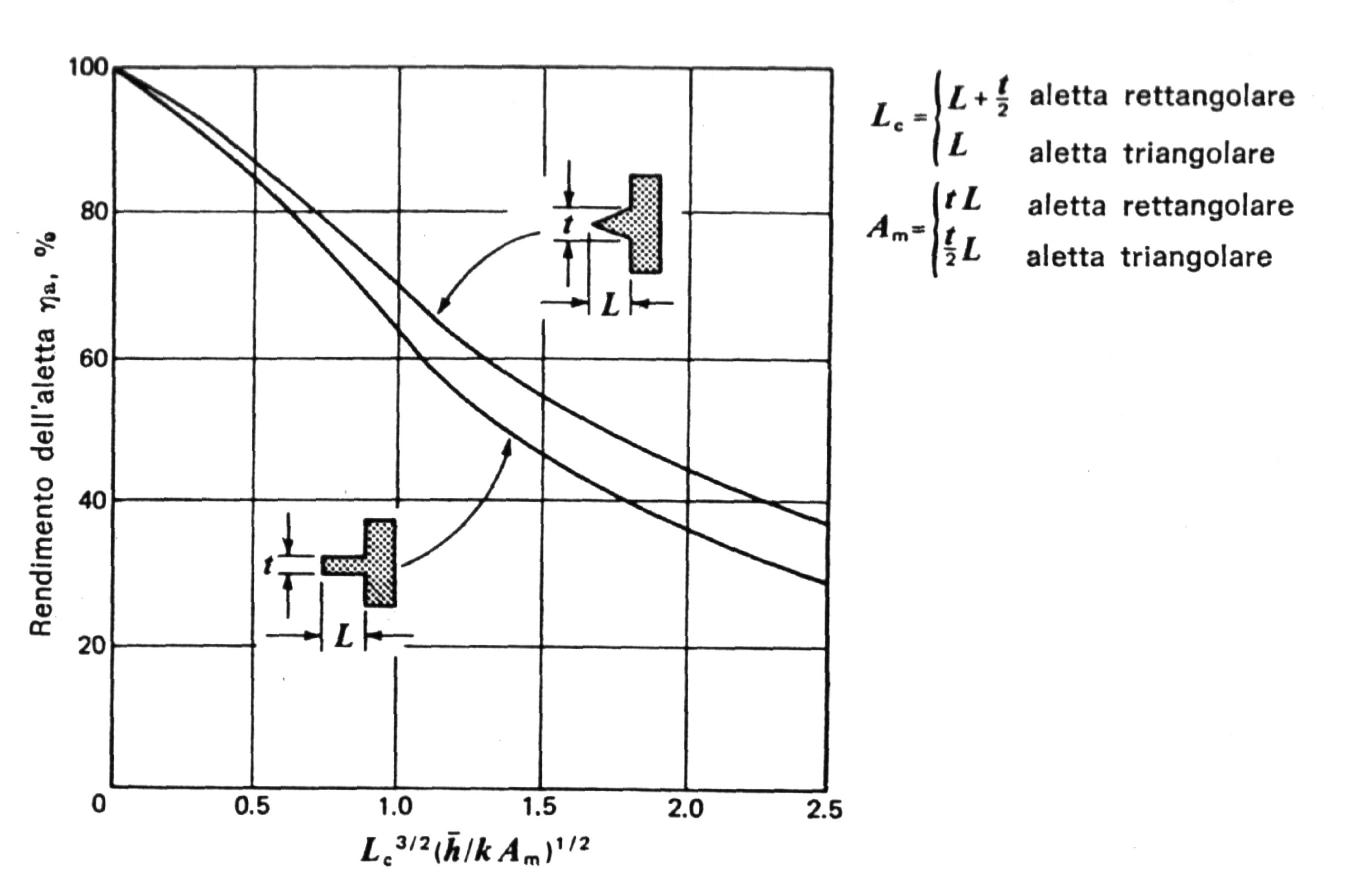
Fig.8 – Efficienza di Alette rettangolari e Triangolari
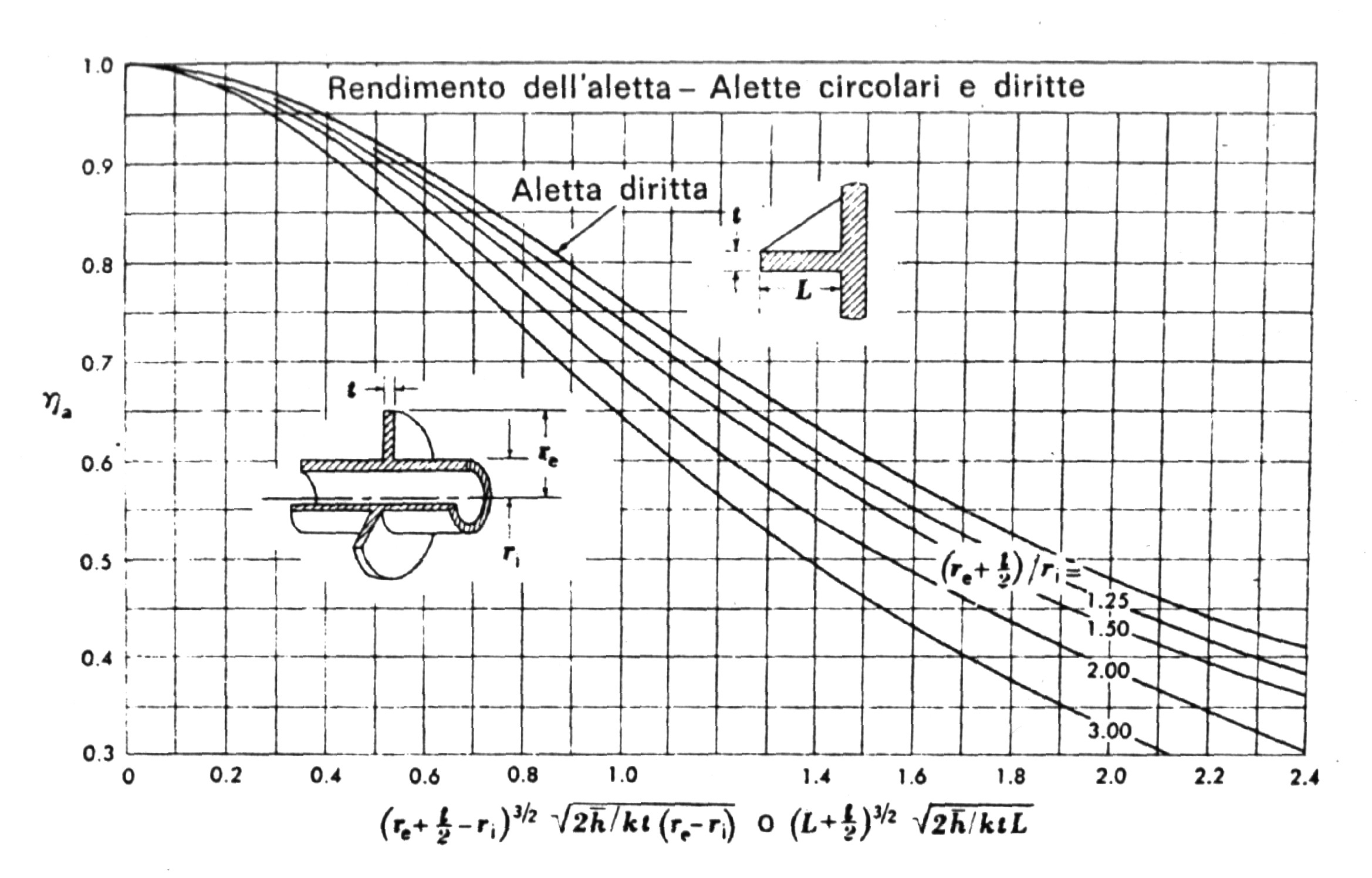
Fig.9 – Efficienza di Alette Circonferenziali a Sezione Trasversale Rettangolare
Sui grafici compare un simbolismo diverso ed in particolare :
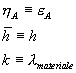
Esercizio: Raffreddamento della CPU di un Calcolatore
Una CPU di superficie quadrata (L=50mm) dissipa una potenza di 20W nell’ambiente (avente temperatura pari 20°C).
Soluzione:
Rispondiamo alla I domanda :
Fig.10 – CPU libera (senza alette)
Si tratta di un caso di convezione naturale in aria e di irraggiamento termico :
![]()
Innanzitutto troviamo il coefficiente di convezione h :
![]()
g=9.81m/s2 è l’accelerazione di gravità
b
=1/T è il coefficiente di dilatazione termica (che nel caso di gas è l'inverso della temperatura).L=0.05m è il lato della superficie quadrata
DT è la variazione di temperatura ![]()
n= 16.10-6m2/s è la viscosità cinematica dell’aria
Gr è il numero di Grashof
Prendendo una temperatura di tentativo TP=100°C otteniamo una temperatura media ![]() ed un valore :
ed un valore :
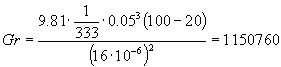
Inoltre il numero di Prandtl è pari a circa Pr=0.71, quindi :
![]()
Tale valore è molto minore di 109 quindi ci troviamo in una situazione di moto laminare e guardando sulle tabelle ricaviamo la seguente formula che ci fornisce il valore del numero di Nusselt, Nu :
![]()
Dal numero di Nusselt ricaviamo allora il coefficiente di convezione h :
![]()
l=0,03 W/mK è la conducibilità termica dell’aria
Resta da determinare ora il coefficiente di irraggiamento hirr :
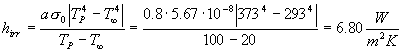
a=0.8 è il coefficiente di assorbimento del materiale (supponiamo plastica nera).
![]() è la costante di Stefan-Boltzmann
è la costante di Stefan-Boltzmann
Quindi ![]()
La potenza termica scambiata è data da :
![]()
quindi si ricava la temperatura a cui si porta la superficie della CPU :
![]()
Tale temperatura è troppo alta e causerebbe il bruciamento dei componenti.
Rispondiamo alla II domanda :
Applichiamo sulla superficie della CPU delle alette di alluminio lunghe 20mm, con uno spessore di 3mm e spaziate 3mm l’una dall’altra.
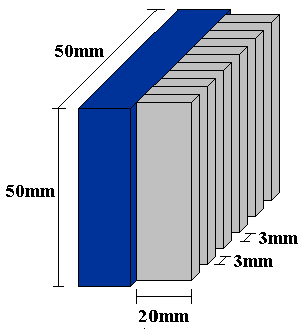
Fig.11 – Applicazione di Alette di Alluminio sulla CPU
Per trovare l’efficienza dell’aletta andiamo a leggere sul grafico della figura 8 l’ordinata corrispondente al seguente valore in ascissa :
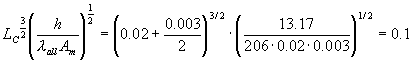
A tale valore corrisponde un’efficienza eA=0.93.
Il numero totale di alette applicabili su un quadrato di lato 5mm è :
NA=parte intera(50/6)=8
Adoperiamo la formula (23), che riscriviamo qui sotto portando a I membro la temperatura incognita TP, per trovare la nuova temperatura a cui si porta la superficie :
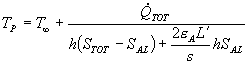
e ricaviamo i valori che ci servono :
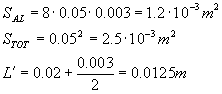
A questo punto andiamo a sostituire ed otteniamo :
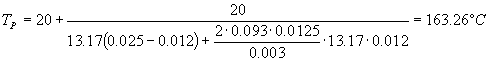
Temperatura molto più bassa rispetto a quella in aria libera.
Nota : Occorre ricordare che tutti i calcoli sono stati svolti trascurando l’effetto frenante delle alette sul moto dell’aria quindi in realtà la temperatura reale sarà più alta di quella trovata sopra.