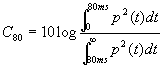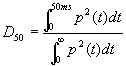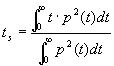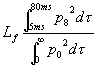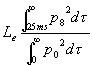Misure acustiche nelle sale
Argomenti trattati :
- Ipotesi sul campo acustico
- Teoria della misura digitale
- Analisi frequenziale
- Segnali MLS
- Segnali sine sweep
- Definizione di parametri acustici
- Appendice A: campionamento dei segnali
Ipotesi sul campo acustico
Il campo acustico in un ambiente
è un sistema lineare tempo invariante; supponiamo che stimolato dal segnale
x(t) reagisca fornendo il segnale y(t). Questa relazione ingresso uscita è
rappresentata da
|
|
y(t) = T[x(t)] |
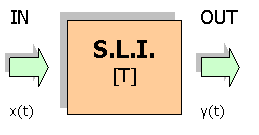
Fig. 1 – Campo acustico in un ambiente.
Se ponendo singolarmente in
ingresso A e B si ottengono rispettivamente le uscite C e D, la proprietà di
linearità assicura che sollecitando il campo contemporaneamente con A e B
si ha la somma C + D in uscita (secondo il ben noto principio di
sovrapposizione degli effetti).
|
IN |
OUT |
|
A |
B |
|
C |
D |
|
A+B |
C+D |
Fig. 2 – Linearità del campo acustico.
Matematicamente un sistema è
lineare se soddisfa la relazione:
|
|
T[a1x1(t) + a2x2(t)] = a1T[x1(t)] + a2T[x2(t)] = a1y1(t) + a2y2(t) " a1, a2, x1(t), x2(t) |
(1) |
La proprietà di tempo
invarianza garantisce che con un dato ingresso si ha la medesima uscita
indipendentemente dall’istante di tempo t in cui avviene la sollecitazione,
cioè la legge di trasformazione T del sistema rimane costante nel tempo
|
|
se y(t) = T[x(t)] allora T[x(t-t0)] = y(t-t0) |
(2) |
Graficamente
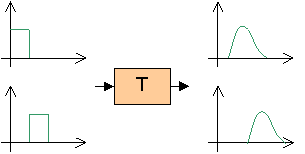
Fig. 3 - Tempo invarianza del campo acustico.
Teoria della misura digitale
I dati entranti nel sistema (IN)
possono rappresentarsi come un vettore di campioni (valori) xi di n
bit ciascuno (nati dal campionamento della sorgente analogica); analoga
rappresentazione si può dare dell’uscita.
Graficamente:
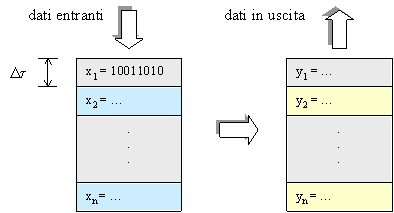
Fig. 4 - Dati digitalizzati.
Si osserva che la
relazione tra i dati in ingresso e quelli in uscita è di tipo particolare;
l’ambiente non risponde immediatamente alle solleciatzioni in ingresso né gli y
tornano a zero quando si smette di fornire x non nulli. Tutto ciò è dovuto alla
memoria del sistema; l’uscita non dipende solo dall’ingresso corrente ma
anche da m campioni precedenti.
Nell’ambito dell’analisi digitale
si può scrivere:
|
|
yn = xnh1 + xn-1h2 + xn-2h3 + … + xn-m-1hm |
(3) |
con xn campione corrente e xn-m-1 ultimo valore di cui il sistema ha
memoria. L’operazione (3) rappresenta una operazione di convoluzione discreta e
si indica
|
|
y = x Ä h |
(4) |
Gli elementi h sono
caratteristici del sistema; questo vettore di lunghezza m è interpretabile come
risultato del campionamento della risposta impulsiva del sistema h(t) ad
una frequenza fc pari a quella usata per i dati in ingresso.
Per definizione
|
|
h(t) = T[d (t)] |
(5) |
con d
(t) elemento neutro dell’operazione di convoluzione (4) denominato impulso
unitario o delta di Dirac ; in ambito digitale d (t) è un vettore
con valore massimo nella prima posizione seguito da tutti zeri:
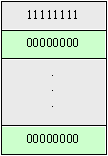
Fig. 5 - d
(t) in ambito digitale.
Dalla (5) risulta che la risposta
all’impulso è l’uscita del sistema lineare tempo invariante quando è sollecitato
dalla d (t)
|
|
infatti y(t) = T[d (t)] = d (t) Ä h(t) = h(t)
(d (t) elemento neutro di Ä ) |
(6) |
Si può pensare di misurare
sperimentalmente i coefficienti hi immettendo nel sistema la d
di Dirac, quindi compionando gli yi
|
|
y1 = 1*h1 + 0*h2 + 0*h3
+ … + 0*hm = h1 |
(7) |
L’apparente semplicità della
tecnica di misura si scontra con la difficoltà nel generare l’impulso unitario
che deve essere brevissimo e di sufficiente potenza (60-80 db sopra il rumore
di fondo).
Si usa in genere l’esplosione di
una pistola caricata a salve che tuttavia genera un segnale lungo 20/40
campioni con più picchi. La situazione migliora se si applica al segnale così
ottenuto un Time Reversal Mirror, tecnica che consiste nel convolvere il
segnale con sè stesso ribaltato nella scala dei tempi. Se utilizzandolo si
ottenesse correttamene una d viste le relazioni (7) e nota la
commutatività dell’operazione Ä si potrebbe procedere nel calcolo dei termini hi
con un generico segnale x in ingresso (esempio del rumore bianco);
ottenuto x-1 (parte problematica di questo approccio)
|
|
x Ä h Ä x-1 = y Ä x-1 = h Ä d = h |
(8) |
Analisi in frequenza
Utilizzando
le trasformate di Fourier si può passare ad analizzare lo stesso problema nel
dominio della frequenza ottenendo:
FFT
|
|
y = x Ä
h |
(9) |
Valutando il numero di operazioni
necessarie nei due casi si osserva che nel dominio del tempo si eseguono m
convoluzioni (m2 moltiplicazioni e m somme) mentre nel dominio delle
frequenze sono sufficienti m moltiplicazioni (a vantaggio dei tempi di elaborazione).La
funzione di trasferimento ingresso-uscita H (quindi i coefficienti h) è data da
IFFT
|
|
H = Y / X |
(10) |
con H valore normalmente
complesso.
Nel caso in cui una o più frequenze
del segnale in ingresso X abbiano coefficienti nulli si ottengono dei picchi
nella funzione H; per ovviare a questo problema si sceglie x con energia su
tutte le frequenze e si mediano i risultati ottenuti su più tentativi nel tempo
(circa cento). Queste ed altre operazioni (FFT, uso di rumore) sono consentite
da programmi specifici come Smaart Pro distribuito con licenza commerciale
dalla JBL.
Segnali MLS
Il segnale MLS (Maximum Length
Sequence) è una sequenza binaria realizzata attraverso uno shift register
(registro a scorrimento):
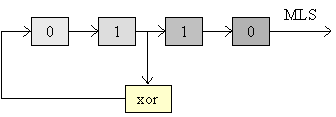
Fig.6 – Struttura a shift register per MLS con N = 4.
Il periodo di un segnale di questo tipo è pari alla lunghezza della
sequenza L
|
|
L = 2N-1 |
(11) |
con N numero di celle dello shift
register; in acustica si usa N pari a 16 o superiore (17, 18) ottenendo 65535 o
più campioni. Il periodo deve essere tale da permettere l’azzeramento del
sistema per evitare l’insorgere di time-aliasing.
Per realizzare una buona sequenza
è necessario porre una certa attenzione nella scelta dei valori iniziali con
cui viene precaricato lo shift register, come del punto di prelievo per
l’ingresso dell’XOR.
I vantaggi di un segnale MLS sono
molteplici:
·
nota a
priori la sequenza generata dal circuito (sono dati i valori iniziali e lo
schema) è facilitato il calcolo del segnale inverso MLS-1 (eseguito
mediante l’inversione di Hadamard)
·
essendo MLS
binario le operazioni di convoluzione si riducono ad una serie di somme (veloci
negli elaboratori) che possono essere realizzate in tempo reale
·
un segnale
di questo tipo ha lo spettro piatto che permette una analisi in frequenza e non
deve essere campionato perché generato direttamente dall’elaboratore.
L’invenzione di questa variante
di analisi risale al 1975 ad opera del tedesco Alrutz; la sua notevole
diffusione fu legata al successo di una scheda costruita dall’americano Douglas
Rife nel 1989. Questa implementava via hardware il circuito di Fig.6,
accelerando notevolmente i tempi di elaborazione, ed era distribuita assieme al
potente software MLSSA (melissa) tuttora utilizzato.
La tecnica esposta non è esente
da svantaggi, in particolare quando il sistema di analisi presenta non
linearità si possono generare echi inesistenti e se non è perfettamente
soddisfatta la tempo invarianza si può avere cancellazione alle alte frequenze
(il solo riscaldamento degli autoparlanti provoca problemi di questo tipo).
Segnali sine sweep
La
tecnica usata correntemente è quella definita sweep. Il segnale è un
seno che parte dalle basse frequenze per arrivare alle alte.
L’inverso dello sweep è lo stesso
segnale invertito sull’asse dei tempi (secondo la tecnica Time Reversal
Mirror); il suo utilizzo richiede però una convoluzione vera cioè maggiore
potenza di calcolo, resasi disponibile solo negli ultimi due anni. Si ricorre
all’analisi in frequenza dove l’operazione di convoluzione è eseguita
attraverso l’algoritmo di Overlap And Save (permette di lavorare su un numero
di campioni dell’ordine di centinaia di migliaia!)
Definizione di parametri
acustici
I
seguenti parametri acustici, tutti definiti dalla norma ISO 3382/97, vengono
utilizzati per determinare la qualità del campo sonoro (risultano molto utili
in ambito musicale).
Viene misurato il suono
riverberato integrato con parte dell’onda diretta (suono utile) quindi
confrontato con la parte seguente nel tempo (più propriamente riverbero) che
sporca la risposta; si ottiene in questo modo l’indice di chiarezza,
nelle versioni C50 e C80. Le cifre che seguono la C sono legate
all’ampiezza della finestra temporale assegnata al suono utile, rispettivamente
50 e 80 millisecondi.
Per definizione
|
|
|
(12) |
dove p è la pressione e il
suo quadrato è impropriamente l’energia.
C50 è espresso in db come
suggerito dalla presenza di 10log nella formula e la sua escursione ottimale è
tra –1 e 1 db; valori inferiori implicano troppo riverbero, superiori un suono
eccessivamente secco.
Analogamente
|
|
|
(13) |
è l’indice di chiarezza con
finestra utile di 80 ms; l’esistenza dei due parametri simili è giustificata
dal differente utilizzo: il primo è destinato all’analisi delle sale per
parlato, il secondo, che a parità di valori permette un suono più ‘impastato’,
è più adatto alla valutazione di sale per l’ascolto musicale.
|
|
|
(14) |
D50 è del tutto analogo al
parametro C50, la scelta dell’uno o dell’altro è pertinente alle preferenze del
tecnico incaricato delle analisi.
Il seguente parametro, denominato
tempo di baricentro ts, prevede una escursione di 30 ¸
80 ms per la voce, e di 50 ¸ 120 ms per la musica.
|
|
|
(15) |
Notevole importanza riveste anche
l’aspetto spaziale del suono (nelle sale di ascolto musicale il pubblico è
avvolto dal campo sonoro) descritto dai parametri Lf lateral
fraction e Le lateral efficiency; entrambi sono espressi
in percentuale. Le misurazioni in questo caso (misurazioni del surround)
vengono effettuate usando un tipo particolare di microfono dotato di due
capsule coincidenti, una omnidirezionale ed una a figura di otto;

Fig. 7 – Andamenti caratteristici di microfoni sferici e
ad otto.
questi microfoni sono dotati di
due uscite chiamate omni e figura di otto, rispettivamente p0 e
p8.
Seguono le definizioni di Lf
e di Le:
|
|
|
(16) |
|
|
|
(17) |
Termina l’elenco dei parametri lo
IACC, inter aural cross correlation, pertinente alle metodiche di
misurazioni giapponesi; in questo caso si usano microfoni binaurali da
indossare sul capo in modo che i due microfoni stereo siano posti in
corrispondenza delle orecchie. Si ottiene l’andamento del campo acustico di un
ambiente convolvendo la sua risposta con una registrazione anecoica, cioè priva
di riverbero.
Appendice A: campionamento dei
segnali
Fissato
n, numero di bit per campione, si divide l’escursione della tensione da
elaborare (segnale analogico) in 2n intervalli elementari, se ne
calcolano i valori medi e si associano alle combinazioni disponibili
(evidentemente 2n) degli n bit.
La fase successiva, il
campionamento vero e proprio, prevede la misura ad intervalli regolari (intervalli
di campionamento) spaziati temporalmente D t
, periodo di campionamento, del segnale analogico; i campioni così
ottenuti sono quantizzati ai valori medi degli intervalli elementari in cui
cadono, quindi trasformati nei numeri binari associati.
Parametri
principali che determinano la qualità del campionamento sono n numero di
bit usati (8 o 16 bit), e fc , frequenza di campionamento
(= 1/D t ), inverso del periodo di campionamento; valori
tipici di fc sono 11, 22 (musicassette), 44 (CD audio), 48khz (DAT),
dove numero più alto indica una maggiore fedeltà del suono digitalizzato
all’originale.
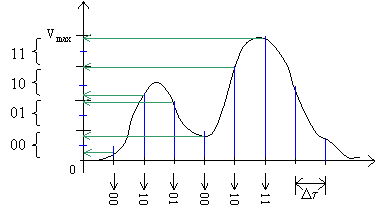
Fig. 8 – Esempio di campionamento a 2 bit.