
INTRODUZIONE
Si supponga di volere eseguire un’analisi acustica su campioni di diversi materiali: una delle grandezze fondamentali che è necessario ricavare è la loro impedenza. Per ottenere tale grandezza si può utilizzare il tubo di Kundt. Esso è essenzialmente costituito da un tubo chiuso, a un’estremità del quale è fissato il campione (opportunamente inserito in un supporto se il materiale è incoerente); all’estremità opposta, a distanza L, vi è un pistone mobile che serve per produrre un treno di onde piane e progressive. Si fissa un riferimento di ascisse lungo l’asse del tubo tale che la sua origine si trovi sulla superficie del campione (così come illustrato in fig.1): si noti che l’ascissa relativa al pistone vale -L.

Figura 1
L’impedenza Z che si sta cercando è una grandezza locale esprimibile tramite la relazione
![]()
che assume in generale valori complessi: non è detto infatti che la pressione (P) e la velocità (u) siano in fase sulla superficie del campione; ciò dipende da caratteristiche intrinseche dello stesso quali la porosità, la cedevolezza e la flessibilità.
Si è detto che Z è una grandezza locale: al fine dello studio in questione ci si interessa pertanto di ciò che succede in prossimità del campione. E’ importante che l << L cioè che la lunghezza d’onda del treno d’onde generato dal pistone sia molto minore della distanza tra il pistone stesso e il campione in modo tale che sulla superficie di quest’ultimo arrivi un regime sviluppato.
MISURA DELL’IMPEDENZA ALL’INTERNO DEL TUBO DI KUNDT
Il treno d’onde generato dal pistone si muove lugo la direzione positiva delle x fino a giungere sul campione sul quale subisce il fenomeno della riflessione (vedere fig. 2).
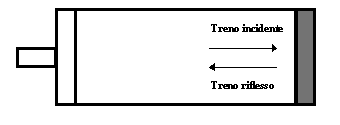
Figura 2
In qualunque ascissa si vada a mettere un microfono, si misurerà un effetto totale dato dalla sovrapposizione di questi due treni d’onda, essendo in presenza di
Passando ad un’analisi matematica del fenomeno, la prima osservazione da fare è che entrambe le soluzioni (quella positiva e quella negativa) dell’equazione di D’Alembert devono essere prese in considerazione.
Di conseguenza il potenziale F della velocità sarà la sovrapposizione di un potenziale relativo alla velocità positiva e di un potenziale relativo alla velocità negativa. Pertanto:
![]()
Per semplicità di notazione viene spesso omesso il termine di dipendenza temporale, fatta l’ipotesi che l’eccitazione imposta dal pistone abbia un regime sinusoidale (altra semplificazione usata implicitamente consiste nell’omettere la specifica Re prima di numeri complessi per indicare che dei valori in questione va presa in considerazione la sola parte reale). La (2) può quindi essere riscritta come
![]()
Dall’espressione del potenziale è possibile ricavare
Per quanto riguarda la velocità si ha
![]()
e per quanto riguarda la pressione
![]()
F + e F - sono due costanti di integrazione per ricavare le quali è necessario imporre due condizioni al contorno:
Derivando la (5) rispetto a x si ha
![]()
in cui è facile riconoscere l’espressione (4) della velocità, da cui
![]()
che può anche essere scritta come
![]()
Essa mette in evidenza una relazione interessante tra P e u; infatti ricordando che w = 2p n (n = frequenza) si può pensare di utilizzare un filtro passabasso per ricavare, partendo da un segnale corrispondente al gradiente spaziale della pressione, un segnale corrispondente alla velocità (nel caso in esame relativo a un sistema monodimensionale il gradiente spaziale si riduce a derivata rispetto alla sola direzione x). Essendo infatti w al denominatore del secondo membro, si ha che tanto più n è alta, tanto più il fattore moltiplicativo è basso: le frequenze più alte del segnale di ingresso risulteranno perciò smorzate.
La soluzione (5) trovata per il campo di pressione non è tuttavia soddisfacente, poichè contiene F + e F - che non sono note sino a che non vengano imposte le condizioni al contorno già indicate precedentemente. Quello che si vorrebbe ottenere è una soluzione formalmente simile in cui la pressione totale P sia espressa in funzione di P+ (modulo della pressione incidente) e P- (modulo della pressione riflessa). Si vuole cioè esprimere la pressione nel seguente modo:
![]()
Si supponga ora che nel tubo vi sia solo il contributo di P+. Si possono allora utilizzare le relazioni già ottenute per l’onda piana e progressiva per esprimere il campo di velocità incidente in funzione del campo di pressione incidente ; analogamente lo stesso ragionamento può essere ripetuto per esprimere il campo di velocità riflesso in funzione del campo di pressione riflesso.
Questo modo di procedere presuppone l’ipotesi di sovrapponibilità degli effetti, secondo la quale il campo sonoro totale è dato dalla somma algebrica dei singoli campi sonori dovuti uno all’onda incidente e uno all’onda riflessa. Questa ipotesi è lecita quando si lavora nell’ambito dell’acustica lineare, quando cioè la risposta del sistema è proporzionale alla sollecitazione che ha ricevuto: il campo acustico è lineare fino a livelli sonori molto elevati (160 dB); nelle applicazioni pratiche è molto raro superare tale limite, quindi l’ipotesi di sovrapponibilità è effettivamente accettabile.
E’ possibile allora, come si diceva, studiare separatamente P+ e P- per ricavare u+ e u- tramite le note relazioni valide per l’onda progressiva. Si ottengono
![]()
![]()
Combinando le due precedenti relazioni e ricordando che u+ e u- sono discordi si ha
![]()
(avendo esplicitato il termine di dipendenza temporale).
Infine dalle (1), (9), (12) si ottiene
![]()
Quindi il valore dell’impedenza varia in relazione all’ascissa x considerata e, in generale, è complesso: l’impedenza del campo di onde stazionarie generata dalla sovrapposizione di un’onda piana progressiva "di andata" e da una di "ritorno" non è costante. Per la singola onda progressiva, invece, si aveva Z = r 0c = cost.
I valori oscillano a seconda delle fasi: l’onda di andata e l’onda di ritorno sono rappresentabili tramite due fasori che ruotano in senso opposto l’uno rispetto all’altro; quando si incontrano in concordanza di fase (entrambi i fasori puntano lo stesso verso) si ha un massimo, quando si incontrano in opposizione di fase (i due fasori puntano versi opposti) si ha un minimo. Si può pensare per esempio a due lancette di orologio che ruotino in versi opposti.
In particolare se |P+| = |P-| il modulo dell’impedenza varia tra 0 e +¥ . Normalmente si ha invece che |P+| > |P-|, cioè che il campo riflesso è più debole di quello incidente: in questo caso il modulo dell’impedenza oscilla tra un valore massimo e un valore minimo senza mai andare a 0 o a +¥ .
IMPEDENZA DEL CAMPIONE E ANALISI ENERGETICA
Si definisce rapporto complesso di riflessione CRF [complex reflection factor] il rapporto tra la pressione riflessa e la pressione incidente, cioè
![]()
E’ possibile esprimere l’impedenza Z in funzione del CRF in un punto particolare, quello corrispondente alla superficie del campione che si sta analizzando. In tale punto si ha che il valore complessivo di Z corrisponde all’impedenza del campione stesso. Essendo x = 0, i termini esponenziali che compaiono nella (13) sono unitari, da cui
![]()
Supponendo invece di non conoscere il valore dell’impedenza del materiale e del CRF, essi possono essere ricavati dalla misura secondo la relazione
![]()
Questa relazione è importante poichè fornisce una relazione tra il rapporto pressione riflessa/pressione incidente e l’impedenza del campione.
Anche per quanto riguarda l’analisi energetica, si ragiona supponendo valida l’ipotesi di sovrapponibilità degli effetti; si considerino separatamente un campo incidente e un campo riflesso che danno luogo rispettivamente ad un’intensità incidente e ad un’intensità riflessa. Allora
![]()
![]()
COEFFICIENTE DI ASSORBIMENTO ACUSTICO
Si supponga di avere un’intensità Iinc incidente contro il campione: in seguito all’impatto con esso, si dividerà in due contributi (fig.3):
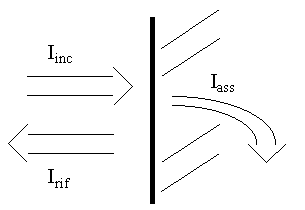
Figura 3
cioè
![]()
dalla quale, dividendo membro a membro per Iinc si ottiene
![]()
dove
![]()
è il coefficiente di riflessione e
![]()
è il coefficiente di assorbimento.
Notare che entrambi sono numeri puri. E’ indifferente conoscere r o a di un materiale (dalla (20) noto uno si ricava l’altro), ma è importante conoscere uno dei due.
Dalle (17), (18), (20) si può scrivere
![]()
Nella pratica ciò che è interessante ottenere è proprio a . Dalla (23) si vede che è quindi necessario conoscere P+ e P-.
Ci si chiede come ricavare questi due valori dalle grandezze che si possono misurare nel tubo di Kundt. Si può misurare in ogni ascissa il valore della pressione totale Ptot tramite un microfono in grado di scorrere lungo l’asse del tubo: l’andamento che si osserva in funzione delle x è del tipo di quello raffigurato nel grafico 1.
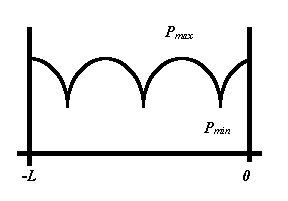
Grafico 1
In esso si possono riconoscere dei punti in cui la Ptot sarà massima e punti in cui sarà minima; sulla parete del campione (x = 0) viene solitamente raggiunto un valore prossimo al massimo. I punti di massimo si hanno dove l’onda incidente e l’onda riflessa sono in fase e i punti di minimo quando le stesse sono sfasate di 180°. Se l’onda riflessa ha la stessa ampiezza di quella incidente (il tubo termina con una parete rigida) allora il valore minimo di Ptot è nullo , r = 1, a = 0. Tuttavia in generale ciò non avviene e anche quando P+ e P- sono in opposizione di fase si osserva una Pmin diversa da 0. Supponendo pertanto di ricavare dalla misura i valori di Pmax e Pmin, si possono scrivere le relazioni seguenti:
![]()
![]()
Esse costituiscono un sistema lineare di due equazioni in due incognite, le cui soluzioni sono:
![]()
![]()
Sostituendo tali valori nella (23) si ha
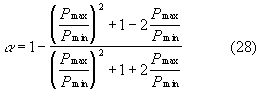
Questa è una relazione fondamentale poichè permette di ricavare a dalla misura di Pmax e di Pmin o del loro rapporto.
Si tratta evidentemente di una soluzione empirica (si ricava il coefficiente di assorbimento a partire da una misura sperimentale); nel grafico 2 è illustrato il grafico che mostra l’andamento del valore del coefficiente di assorbimento in funzione del rapporto tra Pmax e Pmin.
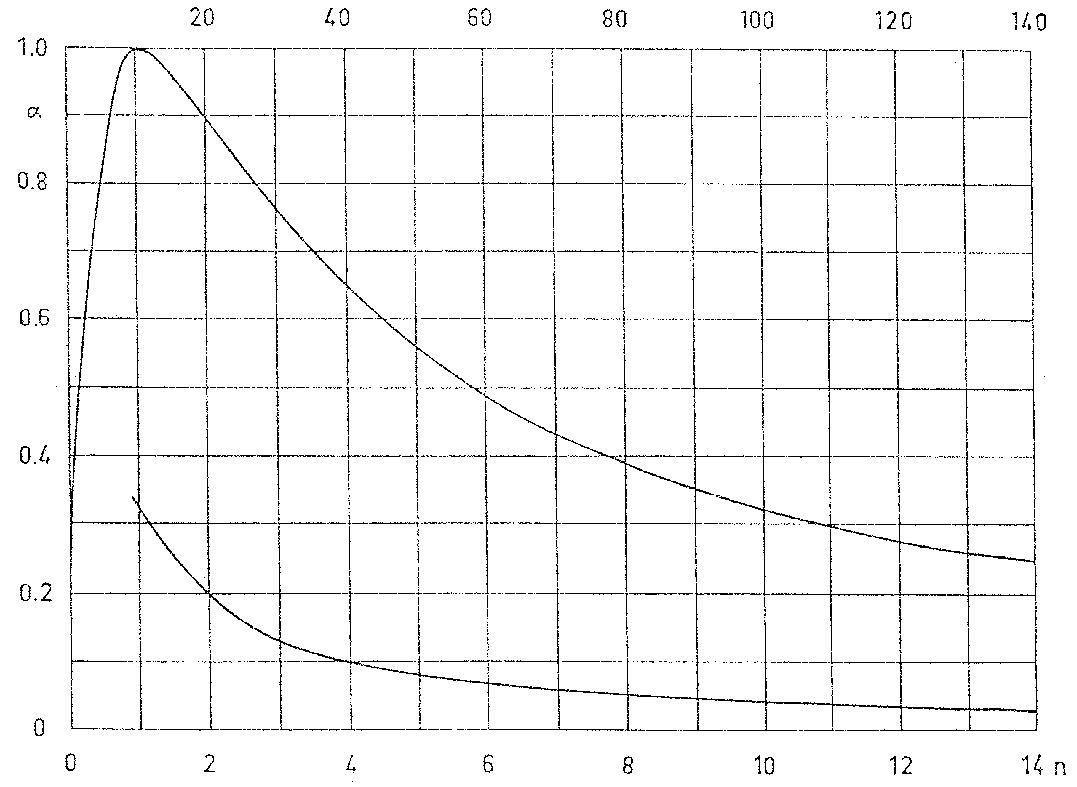
Grafico 2
In tale grafico la curva superiore va letta facendo riferimento alla scala inferiore (0/14); per la curva inferiore si fa invece riferimento alla scala superiore più compatta (10/140).
Si sarebbe potuto anche ottenere una relazione che avrebbe consentito di descrivere analiticamente il valore della pressione in ogni ascissa x del tubo. Tale relazione dà una pressione complessa:
![]()
Osservando che anche CRF è una grandezza complessa
![]()
la (29) può essere riscritta:
![]()
Tale formula mostra effettivamente come varia la pressione totale, in modulo e fase, lungo le x del tubo.
Trovati i moduli di P+ e P- dalle (26) e (27), si può ricavare il modulo dell’impedenza Z del campione tramite la (15). Per ricavare anche la fase si deve tenere conto della fase eij che è funzione delle distanze tra la parete e i punti in cui sono stati riscontrati i valori di Pmin e Pmax essendo tali distanze legate allo sfasamento che l’onda riflessa ha subito rispetto a quella diretta.
Tuttavia la fase dell’impedenza non ha un preciso significato fisico; l’effetto dovuto a un materiale a impedenza complessa equivale a quello di un materiale a impedenza reale spostato a destra o a sinistra rispetto alla posizione in cui effettivamente si trova durante l’effettuazione della misura. Il contributo della fase può essere interpretato come se l’onda riflessa non fosse generata sulla superficie del campione ma a una certa "profondità". Per questa ragione, normalmente si richiede solo il modulo dell’impedenza.
La fig.4 schematizza la costituzione del tubo di Kundt: da notare in particolare il microfono scorrevole tramite il quale effettuare la misura della pressione lungo l’asse del tubo.
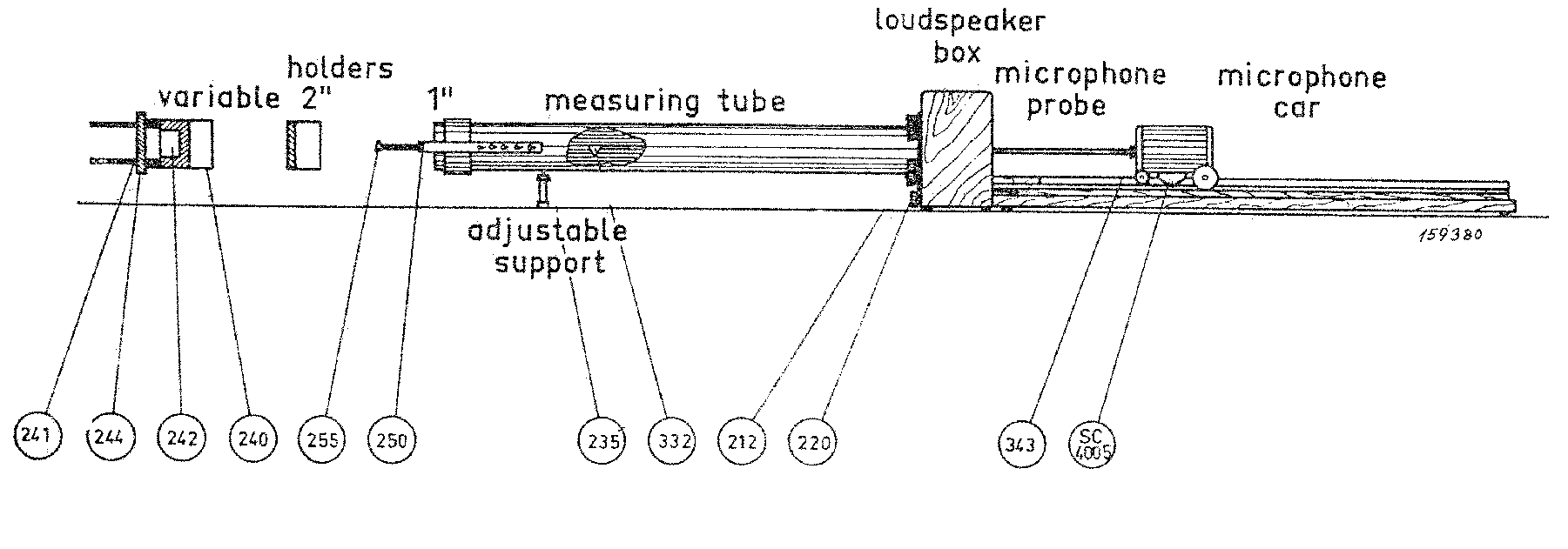
Figura 4
La fig.5 mostra infine un’apparato sperimentale, prodotto dalla danese Bruel & Kjaer, così come lo si utilizzava in passato: sono bene visibili il generatore di forme d’onda sinusoidali e il voltmetro; sulla sinistra sono riportati i grafici di due possibili andamenti della pressione dentro al tubo (quello superiore è relativo a una parete rigida, quello inferiore è il caso più generale).
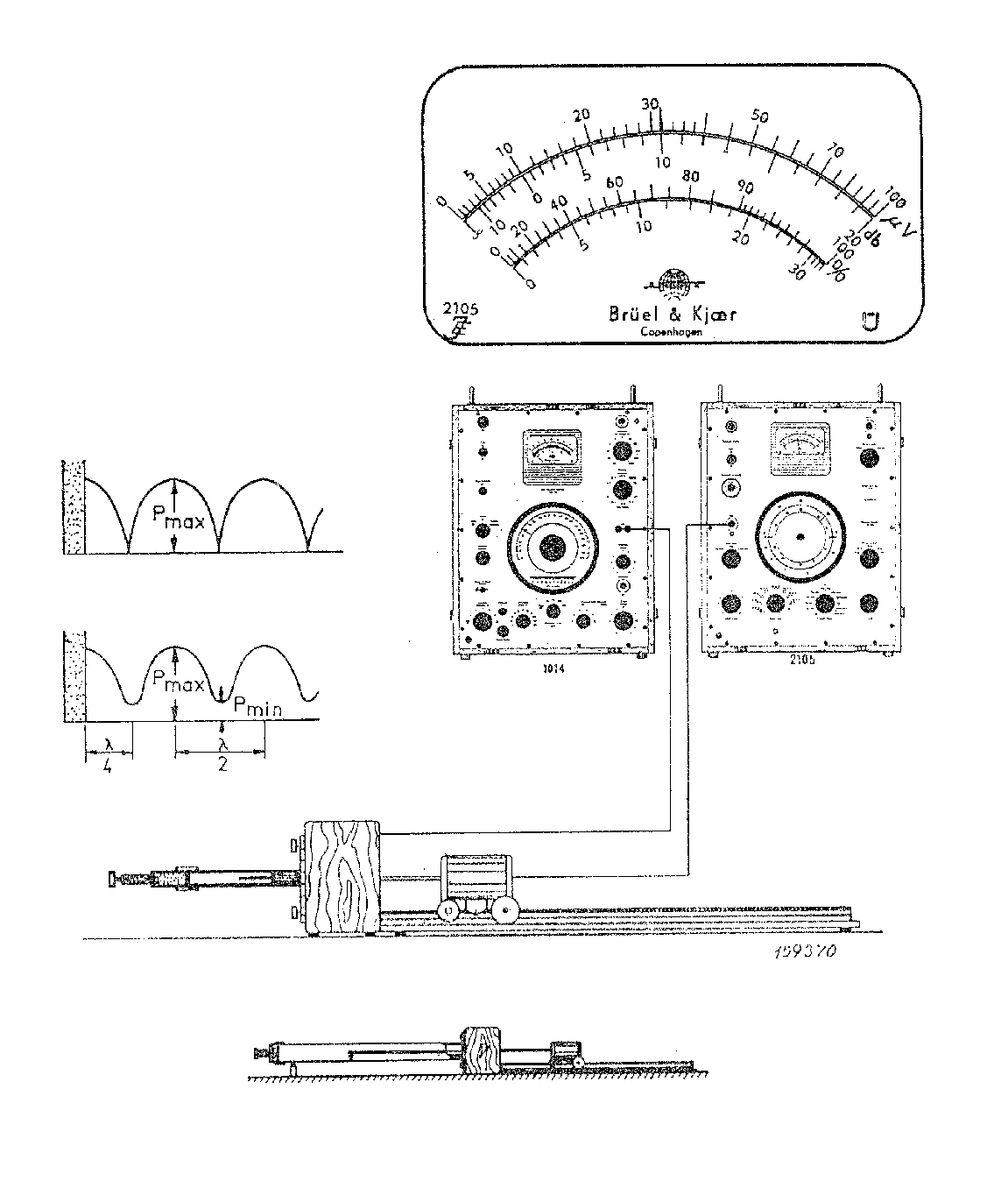
Figura 5
Al giorno d’oggi il tubo di Kundt non viene più utilizzato per almeno due motivi fondamentali:
Esistono tecniche più moderne che si basano su misure in banda larga, cioè che non analizzano una singola frequenza alla volta, ma una banda (intervallo) di frequenze. Gli strumenti matematici che si utilizzano in questi casi sono più complessi della descrizione fasoriale alla quale si è fin qui fatto riferimento.
Tecniche recenti si basano sull’analisi intensimetrica (intensità incidente e riflessa misurate direttamente); questo metodo permette di prendere in considerazione anche onde non piane.
Il tubo di Kundt rimane a tutt’oggi utile a fini didattici poichè costituisce uno dei pochi casi in cui si sa risolvere l’equazione di D’Alembert.
DENSITA’ DI ENERGIA SONORA
Si sono definite le due grandezze di cmpo fondamentali, la pressione e la velocità; si è detto come il loro prodotto rappresenti il trasporto di energia nel mezzo acustico (dà l’idea di propagazione del suono) e di come il loro rapporto rappresenti l’impedenza del mezzo (grandezza importante perchè caratterizzante il campo). Si mostrerà ora come la somma dei rispettivi quadrati sia indicativa della densità di energia immagazzinata nel mezzo acustico.
La densità di energia media si esprime attraverso il rapporto tra energia (E) e volume (V), cioè
![]()
Il valore locale (puntuale) lo si esprime tramite il passaggio al limite per V® 0 del rapporto (32).
Dimensionalmente si esprime evidentemente in J/m3.
Si esamini un caso particolare semplice: quello dell’onda piana e progressiva; si prenda una superficie quadrata di lato 1m attraversata dall’onda (in fig.6 si sono rappresentati i vettori intensità che attraversano tale superficie).
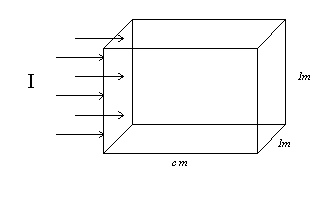
Figura 6
Dato che c è la velocità del suono, in 1 secondo esso percorre c metri. Quindi il volume di spazio percorso dal suono che passa attraverso la superficie in 1 secondo è quello di un prisma avente come base la superficie e come altezza c. Pertanto
![]()
Le espressioni dell’intensità in funzione dei valori RMS [root mean square - valore quadratico medio] di pressione e velocità sono rispettivamente
![]()
e
![]()
Dalle (33) e (34)
![]()
e dalle (33) e (35)
![]()
Queste ultime due relazioni costituiscono, se prese singolarmente, un modello inesatto: la prima esprime la densità di energia attraverso il solo contributo di energia potenziale, mentre la seconda attraverso un solo contributo di energia cinetica. Compendiando queste due relazioni si trova invece il valore reale della densità di energia, costituito da un termine espressione dell’energia potenziale e uno espressione dell’energia cinetica:
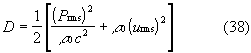
Tale espressione è in accordo con il significato fisico generale di energia (contributi potenziali + contributi cinetici). Quindi è sempre vera: rappresenta cioè orrettamente il fenomeno fisico anche in un caso che non sia relativo a onde piane e progressive.
Si può allora applicare il risultato (38) al caso delle onde stazionarie; l’obiettivo è ancora quello di ricavare il coefficiente di assorbimento a di un materiale posto nel tubo a onde stazionarie. Il problema è quello di trovare Iinc e Irif a partire da P e u, passando per il calcolo dell’intensità totale e della densità. Non è più sufficiente un microfono che misuri la sola pressione, ma è necessario averne a disposizione uno che misuri simultaneamente P e u in un punto del tubo. Ricavate tali grandezze si ottengono:
![]()
A questo punto ricordando l’ipotesi di sovrapponibilità degli effetti, in un volumetto V preso attorno al microfono, sono presenti sovrapposti due treni d’onda, uno incidente (di intensità Iinc) e uno riflesso (di intensità Irif). Allora il valore dell’intensità gia misurato tramite la (39) sarà uguale a
![]()
Notare il segno meno derivante dal fatto che le due intensità sono discordi.
Inoltre dalla (33), ricordando che le densità si sommano come scalari, si ottiene
![]()
La (40) e la (41) costituiscono un sistema lineare di due equazioni nelle due incognite cercate Iinc e Irif. Le soluzioni di tale sistema sono
![]()
![]()
E’ importante notare che non è stato necessario scorrere il microfono dentro al tubo: in qualsiasi punto venga effettuata la misura si ottengono sempre la stessa I e la stessa D.
E’ semplice infine ottenere a :
![]()
Questo è sicuramente il metodo più moderno ed elegante per misurare il coefficiente di assorbimento di un materiale. Richiede peraltro di disporre di una strumentazione più sofisticata rispetto a quella necessaria per l’esperienza descritta in precedenza per la quale occorrevano un solo microfono e un solo voltmetro. Si necessita infatti di uno strumento con almeno due canali di misura, dato che deve misurare simultaneamente u e P; inoltre deve essere in grado di farne il prodotto mediato nel tempo (per ottenere I) e di implementare l’equazione (38) (per ottenere D). La maggior parte degli strumenti di misura normalmente disponibili sul mercato non sono in grado di effettuare quest’ultimo calcolo, il cui risultato va quindi ricavato con altri mezzi.
Il procedimento appena descritto per il calcolo di a è versatile ed efficiente poichè: