
ACUSTICA ED ELETTROACUSTICA
Generalità e Definizioni
INDICE :
Generalità dell’acustica
La disciplina che si occupa dell’acustica ha avuto, ed ha, un enorme importanza a partire dall’anno 1991 in quanto l’Italia governativa ha incominciato ad occuparsi legislativamente del suono.
Questo fatto ha portato al necessario sviluppo di questa disciplina accompagnato dalla proliferazione di sistemi di elaborazione sempre più sofisticati utili per le operazioni di acquisizione e trattamento matematico del suono.
Con la nascita dell’Unione Europea la disciplina scientifica dell’acustica continua la sua evoluzione con la nascita di leggi e decreti atti a regolamentare ogni aspetto inerente il rumore fino purtroppo ad arrivare all’eccesso.
Definizione di Suono
Per meglio capire cosa sia il suono poniamoci in un caso sperimentale come può essere un oggetto che produce rumore all’interno di una sfera di cristallo (Fig. 1) :

Fig. 1 Orologio in sfera di cristallo
Questo esperimento ci permette di fare delle considerazioni riguardo la natura del suono : infatti questo ci permette di dire che se all’interno della sfera di cristallo esiste un mezzo in cui il suono possa propagarsi (ad es. l’aria) questo può propagarsi, invece nel caso in cui l’orologio sia nel vuoto il suono non si propaga all’interno della sfera.
Definiamo allora il suono come una forma di trasporto di energia meccanica, da un punto ad un altro, attraverso una propagazione di onde che richiedono, appunto, l’esistenza di un mezzo elastico : come può essere un gas, un liquido, un solido e quindi non necessariamente l’aria; a differenza di altri fenomeni fisici quali l’irraggiamento che non necessitano di mezzi.
Il suono si propaga tramite delle onde le quali nel loro moto investono particelle di materia che vengono coinvolte nel movimento del suono compiendo delle vere e proprie fluttuazioni, proprio quest’ultime permettono di definire le onde longitudinali in cui il moto delle particelle intorno ad una posizione di equilibrio avviene parallelamente alla direzione dell’onda.
Vediamo di fare un esempio pratico ( Fig. 2 ) per capire le caratteristica di un onda : prendiamo il caso delle onde del mare in cui abbiamo una propagazione delle onde ortogonale alla direzione delle particelle d’acqua : cioè l’acqua si sposta per formare i classici cavalconi mentre l’onda si sposta verso la costa proprio per questo le onde marine prendono il nome di onde trasversali.
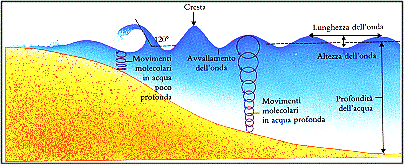
Fig. 2 Esempio di onda marina trasversale
Una domanda che può venirci spontanea è se il suono abbia dei metodi di trasferimento tramite delle onde non sonore : poniamoci nel caso di una persona che parla all’interno di una stanza non insonorizzata, sappiamo tutti bene che la voce può essere udita anche nei locali adiacenti siano essi sopra sotto o a lato della stanza come in Fig. 3 :
Fig. 3 Rumore udibile in ambienti adiacenti
Quindi necessariamente le onde sonore si propagano nelle infrastrutture ( muri, pavimenti, soffitti ecc. ) non più però longitudinalmente ma anche trasversalmente tramite delle onde di taglio , di riflessione solo per citarne due cosicchè nelle altre stanze si possano irradiare.
Nello studio dell’isolamento acustico tanto caro all’attuale legislazione italiana ed europea sarà quindi necessario studiare altri tipi di onde quali quelle trasversali appena viste che si ritrovano anche in un’altra branca scientifica quale la sismologia proprio da questa sappiamo che il movimento di energia avviene secondo due tipi di onde quelle trasversali e quelle longitudinali in cui questi treni d’onda si propagano secondo velocità diverse ( le onde longitudinali sono più veloci delle trasversali e sono proprio queste a determinare le cosidette "scosse di avvertimento" ).
Grandezze fondamentali : Velocità
La velocità di propagazione del suono nei mezzi cosidetti non disperisivi non dipende dal tipo di segnale che si propaga ( dalla forma d’onda ) e nemmeno dall’ampiezza di vibrazione del segnale e si attesta intorno ai 343 m/s nell’aria non variando sensibilmente con la temperatura.
Come si era detto precedentemente la velocità delle onde varia a seconda del loro tipo ( onde longitudinali e trasversali nei terremoti ) ed è necessario distinguerla dalla velocità delle particelle coinvolte nella propagazione.
Proprio per questo poniamoci in un caso particolare riprodotto nell’immagine
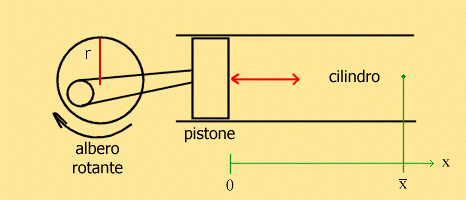
Fig. 4 Esperimento dell’albero rotante
L’esperimento consiste in un albero rotante che si muove secondo una legge sinusoidale con velocità di rotazione w e raggio dell’albero pari a r ( come in equazione (1) ) che viene collegato ad un pistone che si muove all’interno di un mezzo che può essere l’aria.
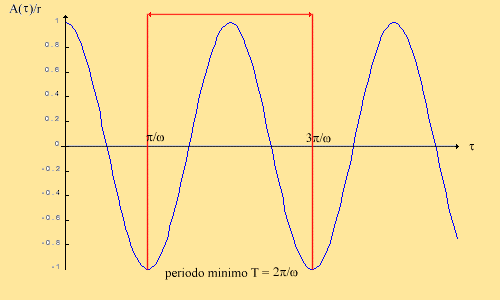
Fig. 5 Grafico delle oscillazioni dipendenti dal tempo
![]() (1)
(1)
Dalla fluidodinamica per ipotesi di aderenza sappiamo che le particelle d’aria attorno al pistone seguono il moto armonico per cui possiamo ricavare la velocità derivando la legge di ampiezza A(t ) :
![]() (2)
(2)
Definiamo per questo tipo di moto due grandezza che lo caratterizzano : il periodo e la frequenza : il primo misurato in secondi "s" che indica il tempo necessario per effettuare un’intera rotazione, mentre la frequenza misurata in "hz" è il reciproco del periodo.
La prima legge armonica studiata in fisica per la sua semplicità è un oggetto attaccato ad una molla : ampliamo il discorso per particelle vicine supponiamo che una particella riceva un movimento elastico tramite una molla, questo movimento si ripercuote su altre particelle come delle molle collegate ad esse come in fig. 6 :
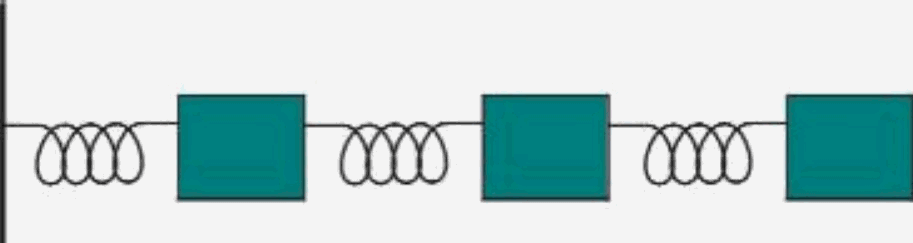
Fig. 6 Masse collegate da molle
Analogamente alla legge precedente vista per le particelle che si muovono attorno al pistone, abbiamo che le particelle ancorate alle molle seguono una legge di velocità come la seguente a meno di un ritardo :
![]() (3)
(3)
Il ritardo di propagazione t rit indica il tempo di ritardo dell’onda sulla particella alla generica ascissa x :
![]() (4)
(4)
La generica posizione risulta :
![]() (5)
(5)
Il ritardo di propagazione può essere ben spiegato attraverso un esempio pratico : prendiamo un aula universitaria lunga 13 metri ed una persona che parla dal fondo della stanza matematicamente il ritardo sarà :
![]()
Come si vede benissimo, anche attraverso le normali esperienze, questo tempo non è tale da far sembrare il suono ed il movimento delle labbra fuori sincronia, ma ponendoci in un contesto di distanza molto più alta, e contando sul fatto che normalmente un uomo parlando pronuncia 3 sillabe al secondo, in una distanza dieci volte più ampia della precedente ( 130 m ) notiamo un ritardo matematico di :
![]()
e quindi uno sfasamento di circa una sillaba.
Fig. 7 Andamento del suono distanza/tempo
L’andamento del tempo del suono è un accorgimento relativamente giovane in quanto fino a 10 anni fa, lo studio del suono era relegato alla frequenza e alla pressione, ma tenendo conto del fatto che il suono può riflettersi e formare delle onde diverse da quelle dirette, e di cui abbiamo fatto i conti per la voce precedentemente, che in genere avranno un ritardo maggiore di quello precedente cosicchè verranno a crearsi delle code che inciderenno sicuramente nell’effetto globale.
Grandezze fondamentali : Pressione
Nel capitolo precedente abbiamo visto che fino a 10 anni fa lo studio dell’acustica riguardava essenzialmente la frequenza e la pressione : per meglio caratterizzare quest’ultima vediamo come si comporta nel nostro caso di moto armonico rappresentativo che è stato il pistone.
Abbiamo visto che parte delle particelle del mezzo elastico attorno al pistone ( nel nostro caso l’aria, ma, come detto, non necessariamente ) partecipano al movimento armonico, comunque solo quelle più prossime al pistone, le altre formano una sorta di muro che si oppone al movimento, questo fenomeno è detto fenomeno del confinamento inerziale cosicchè viene a crearsi una sorta di barriera che crea uno spessore come se fosse solido : questo crea quindi uno sbalzo della pressione del volume in quanto all’avvicinarsi del pistone il volume diminuisce e la pressione aumenta e viceversa quando il pistone si allontana.
Poniamoci in condizioni di gas perfetto e sfruttiamo le ben note relazioni :
![]() (6)
(6)
![]() (7)
(7)
dove i valori a pedice zero rappresentano le condizioni di riferimento.
L’onda sonora non crea degli sbalzi di pressione molto alti se poniamo la pressione standard dell’aria a circa 100.000 pa, l’onda sonora genera uno sbalzo che si aggira intorno a poche unità.
Determiniamo quindi tutti gli strumenti matematici necessari per determinare la pressione e la velocità di un’onda sonora in un generico mezzo elastico; partiamo dalla semplice relazione che lega densità e pressione :
![]() (8)
(8)
Portando a sinistra l’incognita p pressione :
![]() (9)
(9)
Per arrivare ad una relazione ben precisa tra velocità e pressione, modifichiamo la relazione (9) derivandola rispetto alla densità e studiandola nell’intorno di 0 :
![]() (10)
(10)
![]() (11)
(11)
Infine prendiamo in considerazione la relazione (11) il termine a sinistra è dimensionalmente e non addentrandoci in faticose dimostrazioni diciamo che equivale al quadrato della velocità del suono c :
![]() (12)
(12)
estraendo la radice :
![]() (13)
(13)
Queste relazioni appartengono al campo dei gas ponendoci nella sfera dei liquidi abbiamo che :
![]() (14)
(14)
definendo il modulo di compressibilità isoterma per i liquidi :
![]() (15)
(15)
Mentre per i solidi abbiamo che :
![]() (16)
(16)
in cui E definito come il modulo elastico.
Nella tabella che segue sono riportati dei valori caratteristici per alcuni mezzi elastici :
|
Mezzo |
Velocità del suono [m/s] |
|
Acqua |
1480 |
|
Quarzo |
5486 |
|
Acciaio |
6096 |
|
Azoto (N2) (a T = 27°C e p = 1 bar) |
353 |
|
Azoto (N2) (a T = 27°C e p = 100 bar) |
379 |
|
Idrogeno (H2) |
1281 |
Tab. 1 Mezzi e Velocità del suono relative
Soffermiamoci un attimo su alcuni valori riportati nella tabella : come possiamo notare sono riportati due diversi valori della velocità per due condizioni particolari dell’azoto a pressione diversa questo ci rivela che questo gas non segue le considerazioni fatte per i gas perfetti in quanto per essi la velocità non dipende con la pressione.
Per quanto concerne l’acqua abbiamo un discorso che si lega con le scienze belliche e in particolare con i sonar in quanto abbiamo che il suono nel mezzo acqua può percorrere delle distanze molto ampie prima di perdere ampiezza (dell’ordine anche delle centinaia di chilometri ), questo però è sia un risvolto positivo che negativo in quanto la velocità necessaria per raggiungere entrambe le orecchie è identica quindi non è possibile orientarsi con facilità, questo si può ovviare tramite proprio dei dispositivi tipici dei sottomarini che operano in modo da rendere il nostro sistema uditivo in grado di localizzare l’origine del suono anche sott’acqua.
Grandezze fondamentali : Lunghezza d’onda
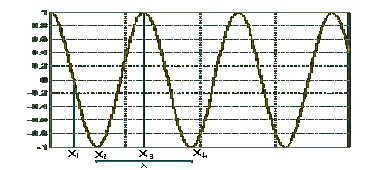
Fig. 7 Onde a profilo Sinusoidale
La lunghezza d’onda è una grandezza propria delle onde sonore che hanno dei profili sinuoidali ( Fig. 7 ) :
Prendiamo in esame 4 punti sulla scala dei tempi e vediamo che in occasione di un tempo generico t abbiamo un valore x1 che è nullo, in un altro il valore x2 che è alla minima ordinata, x3 che assume il valore massimo e x4 di nuovo il valore minimo, quindi possiamo definire la lunghezza d’onda come la minima distanza occorrente per incorrere in due punti aventi ordinata uguale.
Questa definizione ricorda molto da vicino il periodo questo perché la lunghezza d’onda esprime una funzione spaziale mentre il periodo una funzione temporale; queste due funzioni sono legate da una relazione :
![]() (17)
(17)
e ricavando la lunghezza d’onda l :
![]() (18)
(18)
Nella tabella sottostante alcuni valori caratteristici :
|
f |
λ [m] |
|
20 |
17 |
|
1000 |
0,34 |
|
20000 |
0,017 |
Tab. 2 Frequenze e lunghezze d’onda relative
Tornando al problema dell’insonorizzazione un muro ostacola la propagazione dell’onda se è superiore alla sua lunghezza d’onda.
Analisi del Suono
Storicamente il suono era analizzato tramite delle rappresentazioni che si occupavano di pressione e di velocità intese nella loro correlazione con le energie associate : interna sotto forma elastica ( come per la molla ) e cinetica per la velocità.
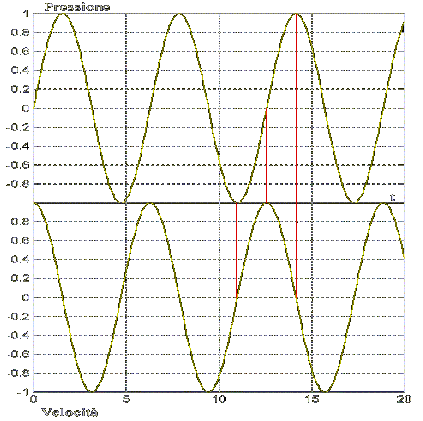
Fig. 8 Andamento Pressione/Velocità
Come si può notare dal disegno vi è un continuo scambio di energia cinetica e potenziale quindi in linea di massima vi è un quantitativo di energia che si conserva.
Per determinare tutti i parametri necessari si utilizzano delle apparecchiature che per quanto riguarda la pressione e per la velocità si chiamano microfoni e anemometri oltre a questi esistono delgli strumenti in grado di determinare le componenti cartesiane singole del vettore complessivo velocità.
Un parametro caratteristico della maggior parte degli studi rappresenta il valor medio della pressione cerchiamo di trovarlo per poterlo utilizzare nei nostri calcoli : questo dato potrebbe essere calcolato tenendo conto di una "fotografia" del segnale corrispondente al tempo di percezione umana che si aggira intorno ai 50 ms :
![]() (19)
(19)
Questo procedimento non ci porta ad un risultato utile in quanto questo valore si attesta a delle oscillazioni intorno al valore p0 quindi inutilizzabile anche perché in ulteriori finestre temporali si mantiene costante.
Sarà necessario quindi ricorrere a dei descrittori che prendano in considerazione gli aspetti energetici del segnale ( quindi velocità e pressione relativi ), facendo questo otteniamo due valori caratteristici denominati valori medi efficaci ( dall’inglese RMS Root Mean Square ) :
![]() (20)
(20)
![]() (21)
(21)
L’abbandono dei sistemi analogici per quelli digitali ci ha permesso di rendere la velocità di calcolo sempre più alta in quanto ormai dei calcoli come la (20) e la (21) sono ormai banali, permettendo un grado di manipolazione del segnale sempre più legato al personal computer e arrivando a frequenze di campionamento anche superiori all’attuale standard dei 44.100 hz della tecnologia CD fino ai 96.000 hz e oltre delle schede sonore PC.
Vediamo in pratica un semplice sistema di analisi analogico molto semplice circuitalmente :
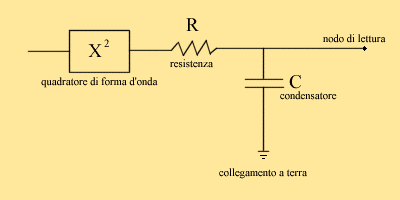
Fig. 9 Circuito analogico RC
Questo sistema non segue le formule presentate al punto (20) e (21) ma tramite una relazione come la seguente :
![]() ,
, ![]() (21)
(21)
Dimensionalmente notiamo che il prodotto RC è un tempo che viene indicato come costante di tempo che ci permette di classificare lo strumento in base al suo valore :
SLOW ð RC = 1s
FAST ð RC = 0,125s
Comparandolo al sistema di analisi uditiva per eccellenza che è il nostro udito possiamo dire che i FAST si avvicinano molto alle capacità dell’uomo.