La lezione seguente verte sulla risoluzione di alcuni problemi inerenti al secondo Principio della Termodinamica. Principio che viene sintetizzato nella formula che segue:

Esso però può anche essere visto nella sua applicazione alla macchina di Carnot e al suo ciclo, infatti dalla condivisione delle due cose si può definire un coefficiente economico della macchina di Carnot pari a:

Da questa legge si nota che il coefficiente dipende dalle sole temperature che influiscono sul ciclo di Carnot. E’ possibile però definire, anche ai fini di una maggiore comprensione di ciò che segue, un’ ulteriore grandezza detta:

Esso è espresso come la divisione del rendimento della macchina termica che si ha in esame e il rendimento della macchina di Carnot che lavorerebbe entro le stesse temperature di quella in esame.

Infatti esso ha la seguente espressione:

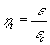
Passiamo ora alla risoluzione degli esercizi proposti dove vedremo l’importanza del secondo Principio.

Testo:

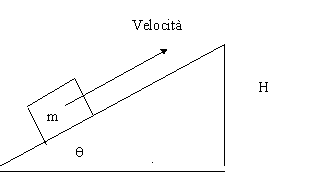
Una locomotiva a vapore si trova ad affrontare una salita mantenendo la sua velocità costante nel tempo. La massa della locomotiva è di 100 tonnellate e procede come detto a velocità costante pari a 80 Km/h. La caldaia brucia 1 tonnellata di carbone ogni ora ad una temperatura pari a 100 °C, la temperatura esterna è di 20°C. La caldaia ha un rendimento pari a 0,25 con un potere calorifico inferiore di 14.000 BTU/lb. Trovare quanto è ripida la salita in termini di angolo di inclinazione (misura dell’angolo q ).

Disegno:

Spiegazioni:

E’ importante prima di partire alla risoluzione del problema far luce su alcuni punti oscuri, come per esempio dire che cosa è il potere calorifico inferiore.

Ogni combustibile ha due poteri calorifici e come è facile intuire sono il potere calorifico inferiore e superiore, la sostanziale differenza tra i due risiede nella quantità stechiometrica di vapor acque che viene utilizzata nella combustione.

Infatti il potere calorifico inferiore è la quantità di energia che viene liberata bruciando una certa quantità di combustibile in presenza di una quantità minima di vapor acqueo, quantità come detto in termini stechiometrici.

Dal grafico che segue si può notare la presenza di una temperatura di rugiada che è importante poichè in quel preciso istante la presenza del vapor d’ acqua in eccesso consente due particolari fenomeni, il primo che si ottiene una diminuzione sostanziale della temperatura dei fumi di combustione sottrendo calore che viene quindi fornito, ecco il secondo fenomeno, dal processo di condensazione del vapore che mutando il suo stato fisico cede energia, questo è un calore latente di condensazione.

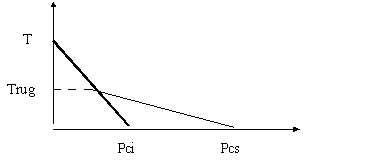
Quindi come detto tutto dipende dalla presenza di vapor acqueo, o meglio il tutto dipende dal tipo di combustibile e dalla facilità che esso ha a liberare acqua nella combustione, di conseguenza la temperatura di rugiada è più alta per combustibili capaci di liberare acqua più facilmente, infatti un combustibile come il metano ha una differenza pari a 0,3 volte.

In alcune caldaie viene recuperata l’ energia ceduta dal vapor acqueo che si condensa, queste caldaie sono dette CALDAIE A CONDENSAZIONE esse hanno un rendimento superiore a 1 circa 1,2/1,3, tutto questo perchè hanno maggiore energia a disposizione recuperata come già detto e sfruttano anche il potere calorifico superiore.

Chiarito questo punto non rimane che far luce su alcune unità di misura che il problema ci pone come per esempio il BTU.

Esso è l’acronimo di British Thermal Unit ed è la quantità di energia che deve essere ceduta per far innalzare di 1 °F la temperatura di una libbra di acqua.

Convertiamo ai fini della risoluzione del problema le unità di misura nel S.I.

1 BTU = 1,055 KJ 1 lb = 0,4536 Kg

Si ottiene che

1 BTU/lb = 2,33 KJ/Kg

Dati:

Temp caldaia = 100 °C = T

m = 100 ton

Temp esterna = 20 °C = t

v = 80 Km/h

Potere calorifico inferiore = 14.000 BTU/lb = Pci

Qm = 1 ton/h

Risoluzione:

Con i mezzi a nostra disposizione ora siamo in grado di risolvere il problema posto infatti possiamo calcolare la potenza sviluppata dalla caldaia che chiamiamo Q con un pedice . essa è pari a:

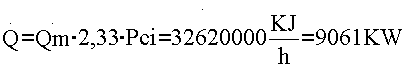
Conoscendo il rendimento della macchina e avendo le temperature di margine possiamo calcolare il coefficiente economico della macchina di Carnot e vale:

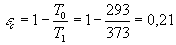
Possiamo dunque ora conoscere il rendimento macchina reale della caldaia ponendo in relazione il coefficiente economico e il rendimento dato dal testo del problema trovando che:

Ora viene facile calcolare la potenza utile che mette in moto la locomotiva che vale:

Importante è porre un’ ipotesi fondamentale ai fini della risoluzione corretta del problema, questa ipotesi è aver già considerato l’attrito delle rotaie e dell’aria compresi nel rendimento termodinamico oppure considerarli trascurabili.

Continuando la risoluzione ora sappiamo che dalla fisica che il lavoro è pari alla differenza di energia potenziale e sapendo che:

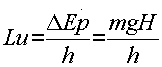
si ricava che l’altezza è:

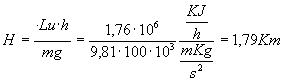
Sappiamo dai dati del problema che la locomotiva percorre in un’ ora 80 Km ed è facile calcolare ora l’angolo scomodando una semplice relazione geometrica esso è pari a:

Gli esercizi che seguono vertono sulla trattazione del lavoro massimo e del lavoro minimo ottenibile e applicabile ad un sistema conosciuto, il primo problema tratta del costo minimo da spendere per estrarre una certa quantità di calore lavorando con una macchina di Carnot, mentre il secondo semplicemente verte sul lavoro massimo ottenibile dal sistema.

Data una macchina di Carnot con un serbatoio alla temperatura Tmin si vuole asportare da esso una quantità di calore pari a Q2 tramite una macchina frigorifera semplice. Sapendo che Tmin è pari a 0,001 K e che Q2 è 1KJ vogliamo trovare a quanto ammonta il costo minimo per poter estrarre Q2 sapendo che il prezzo dell’energia è pari a 150 £/Kwh

Disegno:

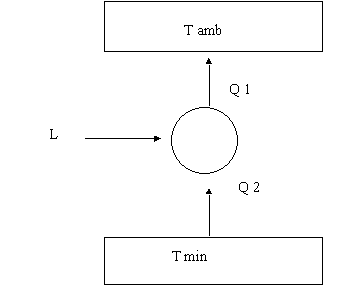
Dati:

Tmin = 0,001K

T amb = 20 ° C

Q2 = 1 KJ

Risoluzione:

Avendo le due temperature è facile calcolare il coefficiente economico della macchina di Carnot esso è pari a:

Dato la grande vicinanza del coefficiente a 1 è importante non arrodondarlo perchè anche piccole variazioni di esso possono introdurre grossi errori che porterebbero a risultati completamente sbagliati.

Dal primo principio della Termodinamica si ha che:

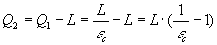
Grazie ad esso troviamo che L min è:

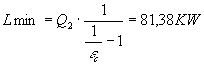
Ora non resta che calcolare il costo minimo moltiplicando il lavoro minimo trovato per il costo dell’energia e ricaviamo che ho un costo minimo pari a 12.208 lit.

Dai risultati possiamo trarre alcune fondamentali considerazioni infatti l’operazione di estrazione da noi compiuta è piuttosto costosa per la misera quantità estratta, il costo sarebbe stato minore se il serbatoio freddo avesse avuto una temperatura maggiore poichè questo si ripercuoteva su un minore coefficiente e quindi minore lavoro di estrazione compiuto.

Il terzo problema tratta come anticipato in precedenza il problema del lavoro massimo ottenibile da un sistema dato, la risoluzione del problema che seguirà sarà data da due particolari metodi, il primo con un procedimento corretto, il secondo tramite considerazioni generali.

Dato un bidone di acqua alla temperatura di 100 °C e del volume di 1 m cubo, esso lavora come serbatoio caldo di una macchina di Carnot che ha serbatoio freddo a T amb = 20 °C. Ci si domanda quanto sia il lavoro massimo ottenibile dalla macchina mantenendo il volume costante.

Disegno:

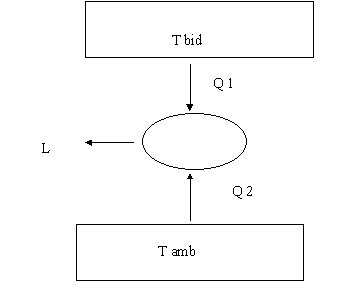
Spiegazioni:

Importante è non affrontare il problema in modo scorretto infatti si potrebbe essere portati a considerare la macchina in nostro possesso come una macchina semplice, ossia come una macchina con due serbatoi a temperatura costante per entrambi mentre essendo il bidone a cedere calore esso avrà quindi una temperatura variabile e non più costante. potrebbe essere utile affrontare ugualmente il problema nel modo sbagliato per ottenere così dei termini comparativi degli ordini di grandezza delle grandezze cercate.

L’ approccio delle temperature costanti porta ad una soluzione del seguente tipo:

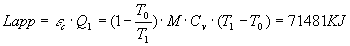
Dove nell’espressione riportata M è la massa del bidone e dove si è considerato un Cv poichè il problema dice che il volume rimane costante nel tempo ed esso è pari a 4,167 KJ/Kg.

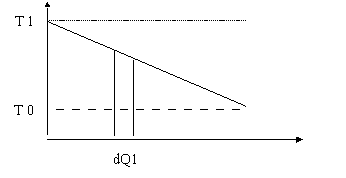
La considerazione fondamentale è che la macchina può essere considerata costante solo per cicli infinitesimali questo perchè come in precedenza accennato la temperatura del bidone cala poichè ad esso è sottratto calore, il coefficiente della decrescita della retta è dato dal calore specifico del bidone.

Logicamente il lavoro massimo si ottiene a processo completamente esaurito, cioè fino a quando non è stato sottratto tanto calore da far calare la temperatura del serbatoio fino a 20 °C cioè fino alla Tamb, e possiamo vedere la situazione considerata osservando il seguente disegno.

Dati:

Tmin = 0,001 K

Tamb = 20 °C

Q2 = 1 KJ

Risoluzione1:

Quindi grazie alle considerazioni precedenti possiamo dire che vale solo:

Dove consideriamo

Questo perchè il problema ci ha suggerito che il bidone non ha variazioni di volume e quindi per la Termodinamica questo significa lavoro nullo su di esso, dal primo principio ci viene la seguente considerazione che: dQ = dU.

Il segno meno dell’ espressione precedente è riferito a decrementi della temperatura che portano a quantità di calore assorbite dal sistema e quindi come detto a variazioni positive di dQ del bidone, cioè si arriva a dire che dQbid = - dQsis, cioè calore ceduto dal bidone è calore assorbito dal sistema e il segno dell’ uguaglianza regola lo scambio.

Portiamoci ora al calcolo del coefficiente che è pari a :

Otteniamo che per ogni ciclo infinitesimo scelto si ha :

Per ottenere quindi il lavoro massimo cercato dobbiamo quindi integrare tra le temperature in nostro possesso e otteniamo:

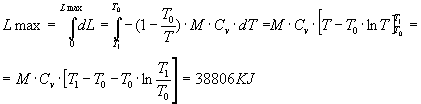
Come si può notare il lavoro trovato poteva anche essere ottenuto con un significativo errore calcolando l’area del triangolo, o meglio come la metà dell’area che si può calcolare tenendo costante la temperatura del bidone e si ottiene un lavoro massimo pari a 36.000 KJ cioè un risultato affetto da un’ errore di circa l’ 8%.

Risoluzione2:

La soluzione alternativa è trovata partendo da alcune considerazioni fondamentali sulla Termodinamica, infatti il lavoro massimo può essere ottenuto se l’entropia dell’universo non cambia, cioè compiendo dei cicli reversibili devo ottenere che:

Dove conosciamo che:

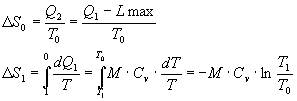
e dove la variazione di entropia della macchina è nulla perchè essa compie cicli reversibili per cui:

Si ottiene quindi combinando le espressioni trovate che:

Ricavando il lavoro massimo ottengo che:

Il quarto e ultimo problema è un’ interessante applicazione del secondo principio per valutare il costo energetico per il riscaldamento di una abitazione, infatti da questa particolare applicazione si è potuto sviluppare sistemi che migliorassero l’utilizzazione dell’ energia e del calore.

Lo scopo è di mantenere una casa alla temperatura costante di 20 °C, usando come potenza 1KW e sapendo che la temperatura esterna è di -5 °C. Vogliamo trovare quanto vale la potenza dispersa.

Disegno:

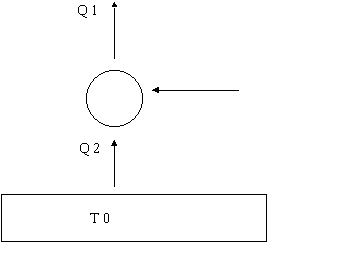
Spiegazioni:

Il problema ha lo scopo di valutare quale sia il metodo migliore per riscaldare l’abitazione in questione e si hanno due modi per farlo:

1 Resistenza elettrica

2 Pompa di calore

Specifichiamo ora alcune grandezze che saranno considerate come il COP o coefficiente di performance, esso non è niente altro che l’inverso del coefficiente economico, si deve poi chiarire che cosa significa CUC (coefficiente di utilizzazione del combustibile) ed è pari al rapporto tra l’energia usata e quella di partenza.

Passiamo ora alla RISOLUZIONE con i due modi comparati.

Con il modo 1 ho una Q dispersa pari a quanta me ne serve ossia Q1 = 1KW

Con la pompa di calore la situazione migliora notevolmente infatti, lavorando tra T0 e un serbatoio a 100 °C possiamo calcolare il coefficiente economico che è pari a:

ottenendo una potenza elettrica pari a:

Si può notare che si ottiene già da ora un bel risparmio.

Però nel nostro ragionamento vi è una piccola imprecisione che ci può far tracciare conclusioni affrettate e questo è il fatto che la potenza elettrica ci deve essere fornita da qualcuno e questo ci viene dalla centrale elettrica oppure da una macchina ciclica installata nell’abitazione che lavora tra due temperature come -5°C e 700 °C, otteniamo una nuova situazione che si schematizza così:

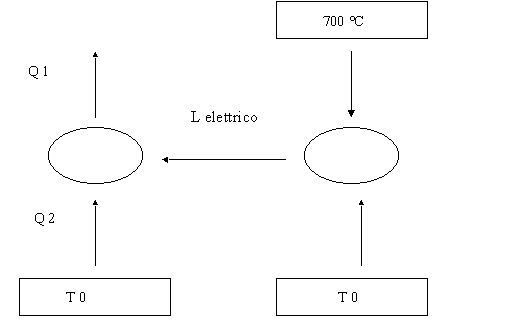
La nuova situazione ci permette di calcolare un coefficiente economico pari a:

e si ottiene una potenza che si deve estrarre dal serbatoio a 700 °C pari al rapporto tra la potenza elettrica e il coefficiente economico ed è pari a 4561,68 W che è comunque un numero sufficientemente piccolo rispetto al 1 KW.

Considerazioni:

Come abbiamo potuto vedere il secondo metodo è notevolmente più efficiente rispetto al primo ma è possibile fare ancora di meglio ed è il sistema adottato a Brescia e sfrutta un principio molto importante che è quello del riutilizzo dell’ anergia che di solito è materiale di scarto.

Infatti costruendo una centrale con lo scopo di produrre acqua calda per tutta la città si è evitato ai cittadini di utilizzare exergia prodotta dalla combustione del metano da parte delle solite caldaie casalinghe, questo porta ad un maggiore risparmio e soprattutto teoricamente non si ha quel tempo di attesa dell’acqua calda perchè questa circola già.

Oltre a tutto questo la centrale produce anche energia elettrica che può essere usata per altri scopi e per altre applicazioni, come questo? Mostriamolo con i calcoli.

Uno schema approssimativo può essere il seguente:

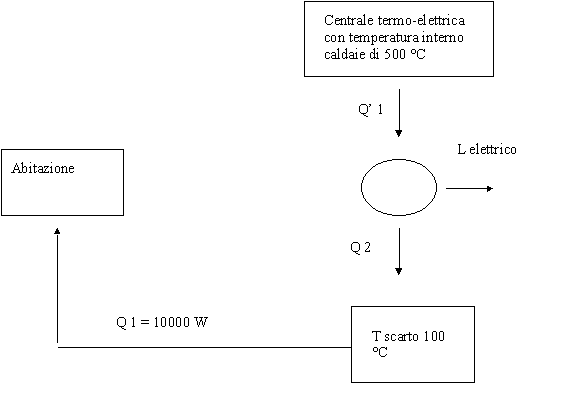
Supponendo la temperatura dell’acqua di scarto a 100 °C e la temperatura delle caldaie di 500 °C si ottiene un coefficiente economico pari a 0,52.

Grazie a questo si ottiene che la potenza ricavata dalla combustione Q500 è:

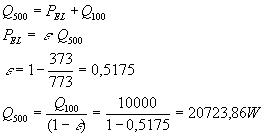
dove Q100 è il precedente valore trovato per scaldare la casa, di conseguenza la potenza elettrica è pari al prodotto del coefficiente economico e Q500 cioè si ottiene combinando le espressioni che la Q500 è pari a 20723,86 W e questo può sembrare poco efficiente ma non si è pensato che questi 10000 W prodotti sono anergia e che oltre a questi ho saputo ricavare una potenza elettrica pari a:

Questo ci mostra come il TELERISCALDAMENTO , così è chiamato questo metodo, introduce dei vantaggi considerevoli sull’ utilizzo dell’energia.