Corso di Fisica tecnica
Docente: Prof. Angelo Farina
Lunedi’ 10-01-2000 Parte prima 8:30 – 10:30
Elaborato di Giambattista Parolari
Matricola n.118391
INDICE:
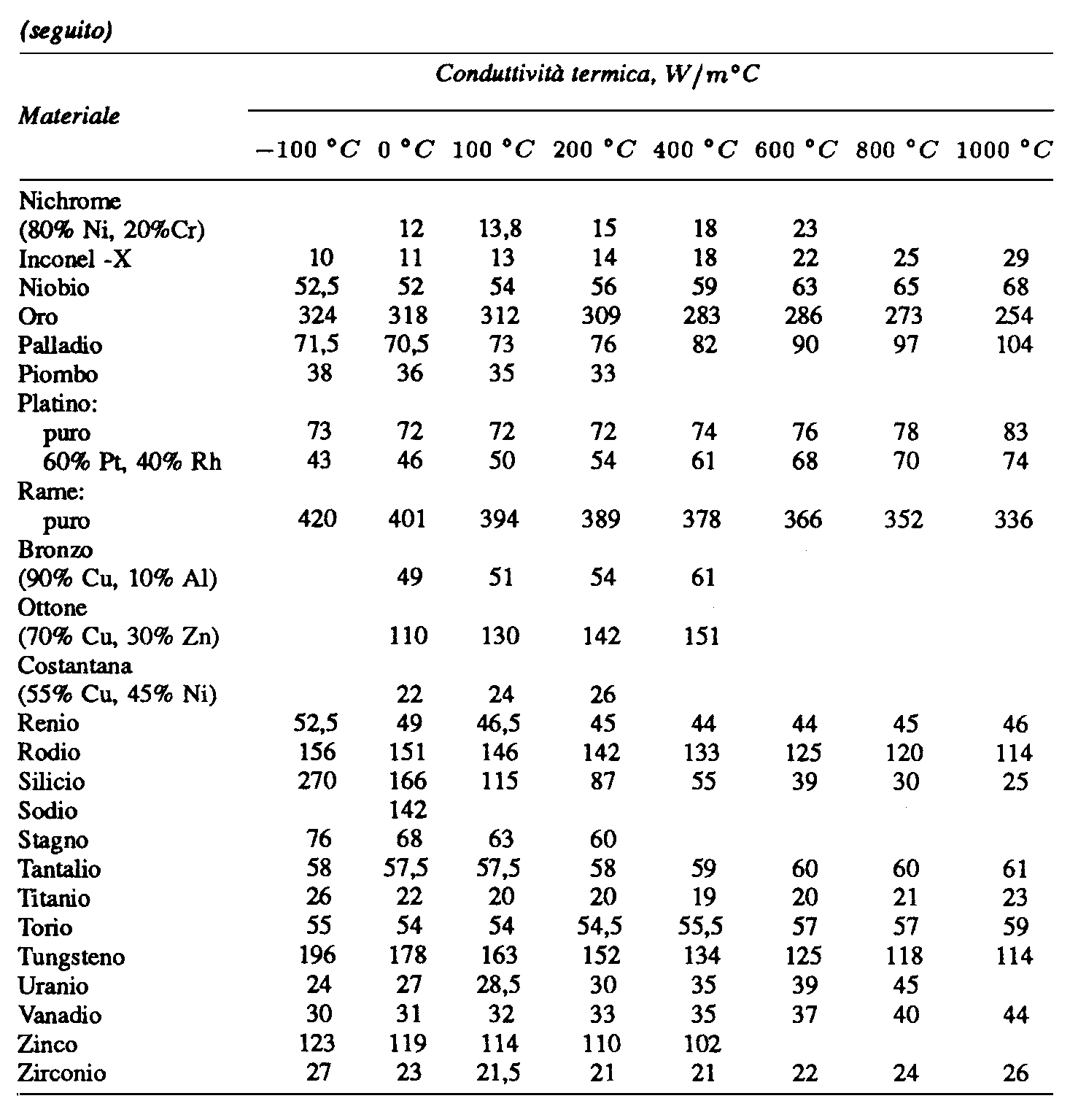
La conduttività termica dei materiali solidi, metallici, e non, dipende in generale dalla temperatura, come si può osservare dai valori riportati nelle tabelle della appendice. In alcuni casi si riscontrano forti variazioni, tali da indurre scostamenti dalle distribuzioni di temperatura ricavate nell’ipotesi di conduttività termica costante.
Per approfondire tale concetto abbiamo ricavato il profilo di temperatura
nel caso di conduzione monodimensionale in una lastra piana, nelle ipotesi
di regime stazionario e in assenza di sorgente termiche. In queste condizioni
particolari l’equazione generale della conduzione
![]()
diventa
![]()
![]()
Dalla fig. 1 possiamo ben notare la differenza tra la soluzione lineare
(ho una retta) dell’equazione di Fourier per l
costante e quella non lineare (ho una curva) della medesima
equazione per lvariabile secondo la temperatura.
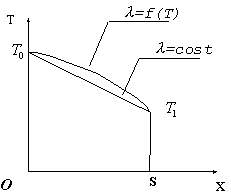
- fig. 1 -
Se lfosse costante, potrei semplicemente
portarla fuori dall’operatore derivata e rimarrebbe una derivata del II°
ordine; in caso contrario, la (2) diventa, dopo aver posto l
= A + BT :
![]()
Grazie alle caratteristiche di linearità e al fatto che i coefficienti
A e B sono costanti, ottengo:
![]()
Tramite una prima integrazione elimino le derivate esterne e individuo
la prima costante di integrazione C1
![]()
Integrando una seconda volta…
![]()
Ho individuato anche la seconda costante di integrazione.
Già dall’eq. 6 capiamo che la temperatura presenta un profilo
del II ordine con termine noto (cioè parabolico). Per
capire in quale posizione è collocata tale parabola applichiamo
le condizioni al contorno:
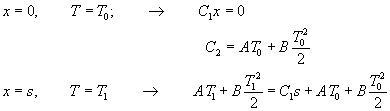
L’equazione finale sul piano (x ; T) sarà, dunque:
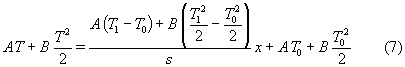
Abbiamo così dimostrato che la funzione che lega la coordinata
x alla temperatura, cioè x = f(T), è
una parabola con asse orizzontale, di cui individuo solo la parte
non tratteggiata in fig. 2:
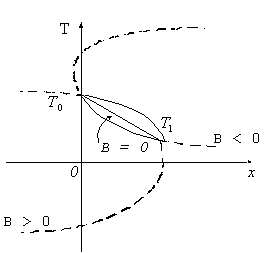
Resta da stabilire se la concavità di tale parabola è
verso destra o verso sinistra; a questo scopo dovrò studiare il
segno del parametro B:
Ulteriori considerazioni si possono fare se riprendiamo la legge di
Fourier:
![]()
Poiché, in condizioni stazionarie, ![]() rimane
ovunque costante, possiamo dire che:
rimane
ovunque costante, possiamo dire che:
la pendenza è minore
la pendenza è maggiore
La dipendenza della conduttività termica ldalla
temperatura risulta fondamentale in sede di progetto della camera
a combustione di una fornace, il cui rivestimento multistrato interno può
essere rappresentato così:
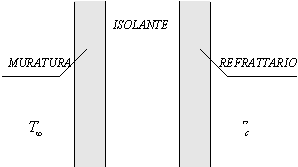
Se la temperatura Tc della caldaia è bassa, allora l
si mantiene piccolo e la funzione di isolante è realizzata; se la
temperatura, invece, diventa molto elevata, l’isolante è sottoposto,
a causa di l (anch’esso cresciuto) ad una temperatura
molto elevata, e se non viene scelto correttamente (in base cioè
ai valori con i quali dovrà lavorare) può sciogliersi, o
addirittura bruciare. Tutto ciò è da attribuire all’elevato
gradiente di temperatura presente all’interno della parete dell’isolante.
Consideriamo un cilindro metallico pieno rivestito con un isolante termico. Sebbene al centro del filo (supposto di rame) io abbia una temperatura lievemente maggiore rispetto al valore sulla pelle dello stesso, posso considerare la temperatura costante data l’elevata conducibilità che presenta questo conduttore. La corrente che lo percorre genera, per effetto Joule, una quantità ci calore che, se non viene eliminata, provoca danni irreparabili all’intero sistema (questo può addirittura incendiarsi…). È proprio questo il limite fisico al massimo valore di corrente che può circolare: il filo nudo presenta grandi difficoltà nello smaltire il calore prodotto e, quasi paradossalmente, una guaina isolante ha questa precisa funzione. In caso di sovraccarico ad esempio, la guaina dissipa tutto il calore in eccesso.
Consideriamo un isolante con conduttività l
che si trova in aria ferma con coeff. di convenzione h (ciò rappresenta
un’ulteriore resistenza termica per il calore).
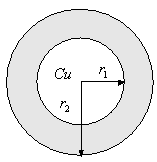
- fig. 4 -
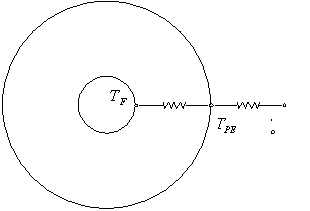
- fig. 5 -
In fig. 4 abbiamo un filo di Cu di raggio r1 avvolto da una guaina isolante tale che il raggio esterno risulta r2.
Indichiamo con
In fig. 5, invece, abbiamo la rappresentazione circuitale di tale sistema: ho due R in serie i cui valori verranno quindi sommati.
Supponiamo che il filo sia lungo L m.
![]()
Al secondo membro della (9) individuiamo:
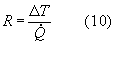
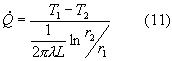
Otteniamo che
![]()
![]()
![]()
Essendo S la superficie esterna…
Otteniamo che
cioè, unendo la (9), la (12) e la (16)
![]()
La potenza che il filo può dissipare attraverso la guaina sarà
allora:
![]()
Tramite la (18) posso ricavare Q da TF e viceversa.
Interessante risulta anche il grafico che lega il raggio r2 dell’isolante
alla potenza dissipata.
Inizialmente l’aggiunta di un isolante provoca un aumento dello scambio termico: il valore di r2 compare al denominatore della (18) per due volte:
L’aumento del raggio dell’isolante, e quindi della superficie di scambio, provoca una diminuzione della resistenza di convezione, e ,almeno inizialmente, un aumento della potenza scambiata, finchè la resistenza di conduzione non cresce abbastanza da compensare la diminuzione della resistenza di convezione.
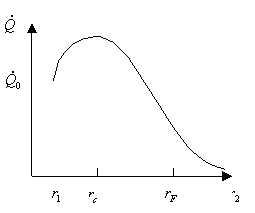
- fig. 6 -
Cerchiamo ora la condizione di funzionamento ottimale, che si ottiene,
analiticamente, trovando fMAX, dato dalla derivata prima nulla:
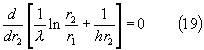
Nella (19) ho eliminato le parti costanti; ricordiamo che dove RTOT,
cioè il denominatore, è minimo, avrò una ![]() massima.
massima.
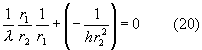
Moltiplico ogni fattore per r2 ? r1
![]()
Ottengo quindi che
![]()
Se avessi un caso con irraggiamento, dovrei modificare il denominatore
della (22) così:
![]()
Superato il valore ottimale ![]() noto una inversione di tendenza: in
noto una inversione di tendenza: in ![]() ho
un punto di flesso a partire dal quale iniziano a prevalere le proprietà
isolanti della guaina. Per la (22), se il coefficiente di convezione
è piccolo e, viceversa, la conducibilità del materiale è
elevata, il raggio critico diviene molto grande (addirittura può
essere 4 o 5 volte il raggio del tubo metallico interno). Per poter
rilevare una diminuzione della potenza scambiata si dovrà oltrepassare
un valore pari al doppio del raggio critico.
ho
un punto di flesso a partire dal quale iniziano a prevalere le proprietà
isolanti della guaina. Per la (22), se il coefficiente di convezione
è piccolo e, viceversa, la conducibilità del materiale è
elevata, il raggio critico diviene molto grande (addirittura può
essere 4 o 5 volte il raggio del tubo metallico interno). Per poter
rilevare una diminuzione della potenza scambiata si dovrà oltrepassare
un valore pari al doppio del raggio critico.
Cerchiamo analiticamente ![]() (il
punto di flesso si ottiene annullando la derivata seconda…). Derivando
la (20) ottengo
(il
punto di flesso si ottiene annullando la derivata seconda…). Derivando
la (20) ottengo
![]()
Moltiplicando ogni termine per ![]()
![]()
Ottengo quindi che
![]()
cioè
![]()
Da questo risultato possiamo intuire l’importanza del valore ![]() :
:
Consideriamo un filo elettrico teso orizzontalmente in una stanza.
sezione A = 1 ![]()
resistenza elettrica ![]() =
1?/m
=
1?/m
i = 5 A
![]() = 20 °C
= 20 °C
hTOT = 50 W/m2K
L = 1 m
- fig. 7 -
Supponendo che il filo non sia avvolto da una guaina isolante, calcoliamo la sua temperatura, cioè TF = ?
La potenza dissipata per convezione risulterà:
![]()
Per effetto Joule posso anche dire che
![]()
Osservando i dati, possiamo ricordare che, in genere, di un filo non
viene fornito il dato relativo al raggio, bensì quello relativo
alla sezione in mm2. Dato che, per un conduttore cilindrico,
![]()
ottengo che
![]()
Tornando all’equazione (A . 1), posso ricordare che S è
la superficie di scambio pari a
![]()
Bisogna stare attenti a non confondere l’area esterna del filo, cioè
quella a contatto con l’aria e attraverso la quale avviene lo scambio termico,
con la sezione del filo stesso. Esplicitando dalla (A . 1) il valore di
TF ottengo che
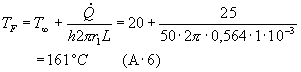
Ovviamente questo è un valore troppo elevato; per questo avvolgo
il filo con una guaina isolante di raggio r2 e conduttività
l = 1 W/m°K. Per ottenere il massimo
scambio termico r2 dovrà essere pari al raggio critico.
![]()
Se confronto r1 e r2, vedo che tale valori sono sproporzionati:
ho una guaina di r = 20 mm che avvolge un filo con r =
0,564 mm. Ciò è dovuto al fatto che ho usato un materiale
con cond. elettrica elevata.
Ricalcoliamo la temperatura del filo TF con questo valore di
r2:
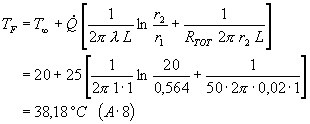
Spostiamo ora la nostra attenzione su un altro aspetto che presenta
numerose applicazione pratiche: l’analisi delle tubazioni. La configurazione
più generica è quella di un liquido (o gas) presente in un
condotto che è posto all’interno di un cilindro cavo, di materiale
isolante, caratterizzato da un rI e una lI
" lT, dove con lT
indichiamo la conduttività del tubo centrale. Quest’ultimo valore
è di norma elevato, essendo il materiale impiegato un metallo.
Introduciamo le seguenti grandezze:
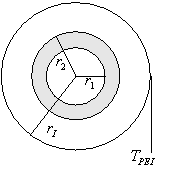
- fig. 8 -
Anche in questo caso abbiamo fornito una rappresentazione circuitale
del sistema: ho 4 resistenze in serie che dovrò poi sommare per
ottenere la resistenza equivalente.
Le 4 resistenze da considerare sono:
![]()
![]()
![]()
Graficamente posso rappresentarle così:
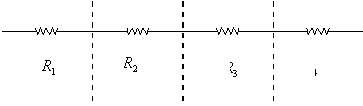
![]()
In conclusione
![]()
Applichiamo le precedenti considerazioni ad un caso pratico. Supponiamo
cioè di avere un fluido all’interno di un condotto rivestito con
un isolante, e che i dati siano i seguenti:

Applichiamo direttamente la (33)
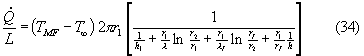
Tale formula rappresenta la densità di flusso di calore per unità
di lunghezza (ho raccolto, a secondo membro, la quantità 2p
r1). Sostituendo alla (32) i valori numerici, trovo che
![]()
![]()
![]()
![]()
Si nota chiaramente quanto poco le R1 e R2 contribuiscano alla somma totale, ma questo dipende dalle caratteristiche specifiche del sistema impiegato.
Sostituendo i valori nella (34) ottengo che
![]()
La stessa teoria vista per i tubi isolati può essere applicata
al caso di una sfera cava avvolta da materiale isolante.
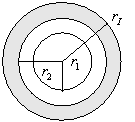
- fig. 9 –
Le quattro resistenze ora saranno:
![]()
![]()
![]()
![]()
La rappresentazione circuitale sara’ :
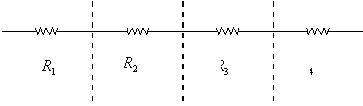
Ricordiamo che
![]()
![]()