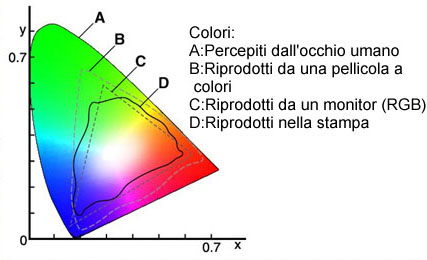
Sintesi Cromatica
Il procedimento di sintesi cromatica è un'applicazione tale che sovrapponendo 2 luci monocromatiche di colore diverso produce un colore diverso dalla luce di partenza.
Esiste un diagramma tale per cui dalla lunghezza d'onda dei due colori da sovrapporre si ricava graficamente il colore risultante.

Per la rappresentazione dei colori si usano diverse tecniche a seconda dell'utilizzo desiderato: la tricromia e la quadricromia sono le due tecniche più comuni.
La tricromia è il metodo di rappresentazione dei colori che utilizza tre componenti fondamentali per ottenere una vasta gamma di colori che ricadono internamente al triangolo RGB( così detto da Red - Green - Blue le tre componenti fondamentali).
La quadricromia utilizza, come il nome stesso lascia intendere, quattro componenti fondamentali la cui mescolanza dà vita ad una vasta scelta di colori che rientrano in una forma delineata dai quattro colori fondamentali.
ESEMPI DI APPLICAZIONI DI SINTESI CROMATICA
ES.1
Monitor del computer
Per visualizzare i colori sul monitor del computer la scheda video utilizza un processo di sintesi cromatica basato sulla tricromia ,sul triangolo RGB, variando le tre componenti fondamentali rosso verde e blu, per ottenere un elevato numero di colori, che non ricoprono comunque tutti quelli visibili.
Ai tre colori fondamentali sono associati in memoria celle di 8 bit per cui ogni colore fondamentale può avere 256 livelli di rappresentazione (colore a 24 bit)
| Prima riga |
R |
G |
B |
| Rosso |
255 |
0 |
0 |
| Verde |
0 |
255 |
0 |
| Blu |
0 |
0 |
255 |
| Bianco |
255 |
255 |
255 |
Nella tabella sono rappresentati i valori dei componenti per ottenere i colori puri, al massimo della loro brillantezza. Per esempio, per avere il rosso mi basta lasciare le due componenti di verde e di blu a zero e il colore ottenuto è sempre il rosso, ma a seconda del valore assunto dal rosso ottengo un colore sempre più brillante.
Tutti i colori interni al triangolo RGB li otteniamo variando i pesi delle componenti fondamentali.
ES.2
Stampa a colori
Nella stampa a colori la tecnica della tricromia è troppo limitante, trovandosi i colori percepibili dall'occhio umano anche esternamente al triangolo RGB ,ma internamente alla strana figura del diagramma, per cui si utilizza la quadricromia.
Inoltre si basa anche su principi di funzionamento opposti rispetto al monitor del computer per cui la sovrapposizione dei tre colori fondamentali, nella loro componente più elevata, mi fornisce il bianco; infatti qui la sovrapposizione dei 3 colori mi fornisce il nero.
Ecco il motivo per cui si definiscono i colori complementari; i complementari di RGB sono quei colori che si trovano diametralmente opposti sulla circonferenza circoscritta al triangolo.
Nella quadricromia i colori fondamentali sono :
nero - violetto - ciano - giallo.
Gli ultimi tre sono i complementari dei tre fondamentali per il triangolo RGB.
I Complementari possono essere trovati pure sul computer tramite la funzione che definisce i colori sullo schermo con un' operazione di tipo XOR, cioè invertendo, nella rappresentazione binaria dei colori, gli 0 e gli 1 .
Nasce però il problema che il complementare, che dovrebbe trovarsi sulla circonferenza, finisce per fermarsi sul triangolo, per i limiti della tricromia, perdendo così le sue caratteristiche di complementare.
NOTA: c'è un ulteriore tecnica più sofisticata di rappresentazione di sintesi cromatica: l'esacromia, utilizzata soprattutto per rappresentare i colori fluorescenti.
Scambio termico tra corpi
Per lo scambio termico tra corpi, mi pongo nella situazione limite di due
superfici poste l'una di fronte all'altra, a temperatura differente T![]() e T
e T![]() formanti una cavità. Da queste basi comuni nascono tre
differenti situazioni :
formanti una cavità. Da queste basi comuni nascono tre
differenti situazioni :
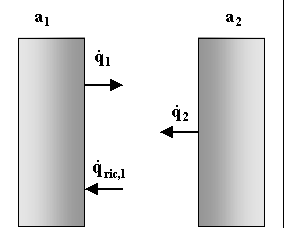
Fig. 1 - Scambio termico tra due corpi neri
![]() =
= ![]() =1
=1
La superficie 1 emette una quantità di calore pari a ![]() ,che rappresenta il potere emissivo integrale, che viene interamente
assorbito dalla parete 2. Analogo discorso per la superficie 2.
,che rappresenta il potere emissivo integrale, che viene interamente
assorbito dalla parete 2. Analogo discorso per la superficie 2.
Utilizzando la relazione di Prevost e la legge di Stefan - Boltzmann poiché siamo in presenza di due corpi neri avrò :
![]()
![]() ( 1 )
( 1 )
![]() =
=![]() perché il corpo nero non assorbe.
perché il corpo nero non assorbe.
Il corpo grigio 1 di tutto il calore emesso ![]() dalla parete 2 ,assorbe unicamente
dalla parete 2 ,assorbe unicamente ![]() e riflette
e riflette ![]() che torna sul corpo 2 sommato alla quantità
che torna sul corpo 2 sommato alla quantità ![]() emessa da 1.
emessa da 1.
Quindi sul corpo 1 arriva complessivamente la quantità :
![]() (2)
(2)
![]() (3)
(3)
Il primo termine rappresenta la quantità che emette la parete 1,emette meno
rispetto al caso di corpo nero, mentre il secondo termine rappresenta quel che
gli piove addosso e che riesce ad assorbire (![]() ).
).
Ecco il caso più complicato, ciascuna delle due pareti emette per i fatti suoi, però ciascuno oltre ad emettere riflette.
![]() è la potenza complessiva che incide sulla faccia 1, così come
è la potenza complessiva che incide sulla faccia 1, così come ![]() è la potenza complessiva che incide sulla parete 2.
è la potenza complessiva che incide sulla parete 2.
(1-![]() )
) ![]() viene riflessa e sommata a
viene riflessa e sommata a ![]() per dare
per dare ![]() .
.
Analogamente accade per ![]() ,in parte riflessa
,in parte riflessa ![]() e si somma a
e si somma a ![]() .
.
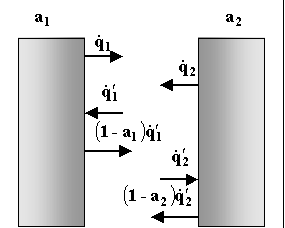
Fig. 2- Scambio termico tra due corpi grigi
![]() (4)
(4)
![]() (5)
(5)
Devo risolvere il sistema per poter poi sostituire nell'espressione di Prevost sulla potenza scambiata alla superficie 1.
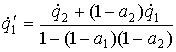 (6)
(6)
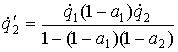 (7)
(7)
Sostituendo nella relazione di Prevost relativa alla parete 1 l'equazione (6) ottengo l'equazione generale che comprende anche i due casi precedenti di superfici entrambe nere e una nera e l'altra grigia:
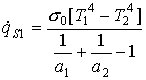 (8)
(8)
La (8) è la relazione rappresentativa dello scambio termico tra due superfici piane parallele indefinite grigie.
Tuttavia non rappresenta l'intera potenza scambiata tra le superfici, infatti dobbiamo tenere conto dello scambio termico per convezione essendo presente tra le lastre un fluido.
![]() (9)
(9)
Il primo termine della (9) rappresenta la resistenza di convezione, che è lineare con la temperatura, mentre il secondo termine dev'essere riportato ad un'espressione lineare; per fare ciò lo sostituisco con
![]() (10)
(10)
da cui, uguagliando la (8) con la (10) ottengo
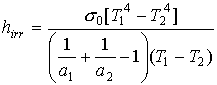 (11)
(11)
Ecco allora che si nota chiaramente come il coefficiente di irragiamento dipenda fortemente dalla temperatura, molto di più di quello di convezione, per cui lo si deve utilizzare solo conoscendo già i valori di temperatura e spostandoci di poco da quei valori essendoci una dipendenza dalla quarta potenza della temperatura.
Fattori di vista o di forma
Introduco i fattori di vista per poter trattare superfici più complicate delle lastre piane parallele affacciate
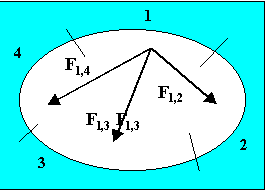
Fig. 3 Fattori di forma per superfici affacciate
In questo caso mi trovo di fronte ad una superficie chiusa convessa costituita da 4 parti indipendenti; la potenza totale per la superficie 1 è
![]()
Mi chiedo qual è la parte di potenza emessa dalla superficie 1 che va a
finire su 3, perché ovviamente non tutta la potenza emessa deve per forza finire
proprio sulla superficie 3, la indicherò con ![]() , da cui definisco il fattore di vista come :
, da cui definisco il fattore di vista come :
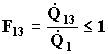 (12)
(12)
Abbiamo in questo modo definito il fattore di forma che nel caso precedente di lastre piane parallele affacciate era
![]()
poiché la somma delle potenze emesse dalla superficie 1 e che vanno alla
j-esima superficie mi dà la potenza totale emessa dalla superficie 1 stessa, allora
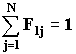
NOTA: esiste pure il fattore di forma riferito alla superficie stessa :![]() .
.
Fattore di forma nel caso di due superfici una interna all'altra
Normalmente è molto complicato calcolare i fattori di forma, ci sono sui
libri casi già calcolati e da utilizzare in caso di bisogno; uno di questi casi
notevoli di cui faremo uso spesso è quello in cui una superficie grande e chiusa
![]() contiene
contiene ![]() ,superficie convessa per evitare che esista
,superficie convessa per evitare che esista ![]() .
.
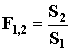 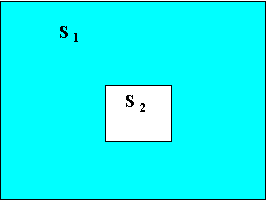 |
Fig. 4 Fattore di forma di un corpo che ne abbraccia un altro
I due corpi sono isotermi e per calcolarne il bilancio energetico supponiamo che siano neri
![]() (13)
(13)
![]() (14)
(14)
Per ipotesi d'equilibrio termico uguagliamo a zero il calore scambiato dalla superficie 2 nell'equazione di Prevost
![]() =0
=0
Da cui ricavo il fattore di forma di un corpo che ne abbraccia un altro:
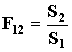 (15).
(15).
Nel caso generico di due corpi grigi con coefficienti d'assorbimento ![]() e
e ![]() , non isotermi, imposto il calcolo come nel caso precedente delle due
lastre grigie parallele affacciate utilizzo le medesime equazioni ricordando
però che le potenze emesse non sono per unità di superficie
, non isotermi, imposto il calcolo come nel caso precedente delle due
lastre grigie parallele affacciate utilizzo le medesime equazioni ricordando
però che le potenze emesse non sono per unità di superficie ![]() e
e ![]() ,ma
,ma ![]() e
e ![]() , mentre
, mentre ![]() e
e ![]() sono le potenze ricevute dalle singole pareti e sostituendo questi
valori nelle equazioni (4) e (5) e tenendo conto dei fattori di forma ottengo il
sistema:
sono le potenze ricevute dalle singole pareti e sostituendo questi
valori nelle equazioni (4) e (5) e tenendo conto dei fattori di forma ottengo il
sistema:
![]() =
=![]() (16)
(16)
![]() =
=![]() (17)
(17)
Da cui ricavo, risolvendo il sistema di due equazioni :
![]() =
=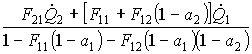 (18)
(18)
E lo sostituisco nella relazione di Prevost insieme alla (13):
![]()
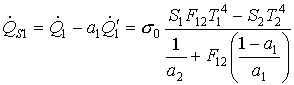 (19)
(19)
L'equazione (19) rappresenta l'espressione più generica per la potenza
scambiata nel caso di due corpi grigi uno interno all'altro, a temperature
diverse e con ![]() non troppo piccolo rispetto al corpo
non troppo piccolo rispetto al corpo ![]() ;infatti se
;infatti se ![]() è molto piccolo avremmo
è molto piccolo avremmo ![]() << 1 e otterremmo dalla (19)
<< 1 e otterremmo dalla (19)
![]() (20)
(20)
essendo ![]() << 1 dal momento che
<< 1 dal momento che ![]() è molto piccolo.
è molto piccolo.
Esempio
Un uomo interno ad una stanza lo posso considerare come una superficie interna ad una superficie nera anche se le pareti sono pitturate di bianco.
Esercizi relativi allo scambio termico
Esercizio 1
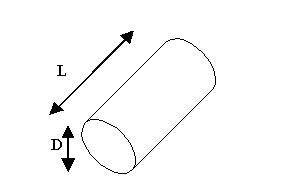
Forno rotante per la cottura del cemento: consiste essenzialmente di un cilindro che ruota intorno al suo asse.
![]()
Fig.5 Forno rotante per la cottura del cemento
L = 5 m
D =1.5 m
a=0.8
![]() = 523 K
= 523 K
![]() = 300 K Rappresenta la temperatura dell'ambiente attorno al forno
= 300 K Rappresenta la temperatura dell'ambiente attorno al forno
![]() = ?
= ?
Il problema ci richiede di determinare la potenza termica per irragiamento del forno
![]() =
=![]()
E' una potenza elevata che devo dare incessantemente al forno tramite un
riscaldatore per mantenerlo in temperatura; allora si cerca di ridurre questo
![]() mettendo un foglio di lamiera zincata di resistenza termica
trascurabile.
mettendo un foglio di lamiera zincata di resistenza termica
trascurabile.
a=0.4 è il suo coefficiente d'assorbimento
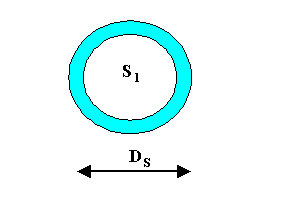
Fig.6 Forno per la cottura del cemento avvolto da una lamiera (sezione)
![]() rappresenta il forno,
rappresenta il forno,
attorno a cui sistemiamo
il foglio di lamiera zincata
il cui diametro è
![]() =2.25 m
=2.25 m
Il forno questa volta scambia con lo schermo a una temperatura non nota, per cui esistono ora due incognite da determinare ,la temperatura dello schermo e la potenza scambiata.
Scrivo il circuito elettrico equivalente
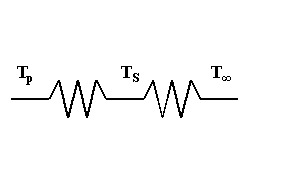
La prima resistenza rappresenta lo scambio tra forno e schermo, mentre la seconda rappresenta lo scambio tra schermo e ambiente
Per lo scambio termico tra schermo e ambiente posso ancora mantenere valida la supposizione precedente di vedere il sistema come 2 superfici una interna all'altra e di applicare l'equazione (19)
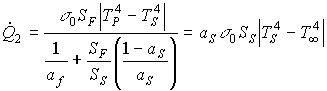 (20)
(20)
Grazie alla seconda uguaglianza l'unica incognita rimane ![]() per cui
per cui
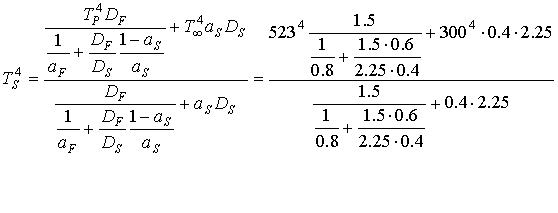
![]()
Adesso vado a sostituire il valore di ![]() calcolato sopra, nell'espressione della potenza scambiata (20)
calcolato sopra, nell'espressione della potenza scambiata (20)
![]()
Esercizio 2
Devo calcolare la temperatura che raggiunge una piastrella quadrata di 50 cm di lato, posta in un terreno isolante che non scambia calore per induzione.
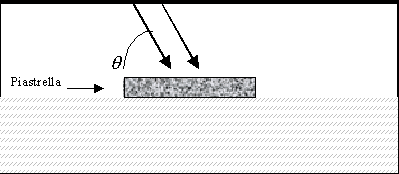
Fig. 7 Piastrella posta in un terreno isolante
Ci sono forniti dal problema i seguenti dati:
![]()
a=0.8
![]()
![]()
![]() rappresenta la temperatura vista dalla mattonella all'aperto.
rappresenta la temperatura vista dalla mattonella all'aperto.
a è il coefficiente d'assorbimento della piastrella, il suo valore indica che
è piuttosto nera; mentre ![]() rappresenta la conducibilità dell'aria, valore che ci tornerà utile nel
calcolo dello scambio convettivo.
rappresenta la conducibilità dell'aria, valore che ci tornerà utile nel
calcolo dello scambio convettivo.
Infine i raggi solari incidono sulla piastrella con un angolo ![]() .
.
L'esercizio ci richiede di determinare la temperatura della piastrella ![]() ; posso supporre che sarà superiore a
; posso supporre che sarà superiore a ![]() che è quella dell'ambiente esterno .
che è quella dell'ambiente esterno .
Calcolo ora la potenza che incide ma che non viene assorbita
![]() (21)
(21)
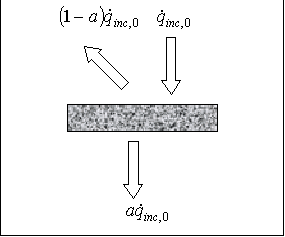
Fig.8 Potenze relative alla piastrella
![]() rappresenta la potenza assorbita dalla piastrella; l'equazione
risolutiva sarà
rappresenta la potenza assorbita dalla piastrella; l'equazione
risolutiva sarà
![]() (22)
(22)
Vado ora a calcolare il valore del coefficiente di convezione calcolando il valore del numero di Nusselt ,Nu, legato ad h dalla seguente relazione:
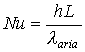 (23)
(23)
Inoltre lego Nu ad altri due numeri ![]() numero di Grashof, e
numero di Grashof, e ![]() numero di Prandtl, attraverso la relazione di Fischenden e Saunders
numero di Prandtl, attraverso la relazione di Fischenden e Saunders
![]() (24)
(24)
A questo punto per calcolare il valore di ![]() ho bisogno di conoscere il valore della temperatura della piastrella,
ecco che devo utilizzare il metodo di risoluzione "a tentativi" nel senso che
devo azzardare dei valori di temperatura e inserirli nella formula di
ho bisogno di conoscere il valore della temperatura della piastrella,
ecco che devo utilizzare il metodo di risoluzione "a tentativi" nel senso che
devo azzardare dei valori di temperatura e inserirli nella formula di ![]() e vedere se sostituendo nella (22) il relativo valore di h che
calcolo trovo un valore di temperatura molto simile.
e vedere se sostituendo nella (22) il relativo valore di h che
calcolo trovo un valore di temperatura molto simile.
Il valore di primo tentativo sarà:
![]()
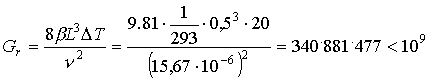 (25)
(25)
Vale a dire che essendo ![]() minore di
minore di ![]() ,il moto è laminare e vale la formula di Fischenden e Saunders (24)
con
,il moto è laminare e vale la formula di Fischenden e Saunders (24)
con
C = 0.14
a = b =0.3
![]()
Ora utilizzo la relazione (23)
h=![]()
Adesso prendo la relazione (22) e vado a vedere il valore di ![]() sostituendo il valore di primo tentativo non nel termine elevato alla
4, ma nel termine lineare
sostituendo il valore di primo tentativo non nel termine elevato alla
4, ma nel termine lineare
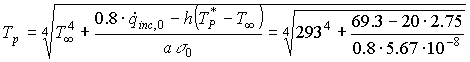
![]()
Il valore di temperatura della piastrella calcolato si discosta troppo dal valore di primo tentativo utilizzato nella relazione (25), ecco che devo inserire nella (25) un secondo valore di temperatura e andare a ripetere i calcoli e vedere se i due valori si avvicinano per cui
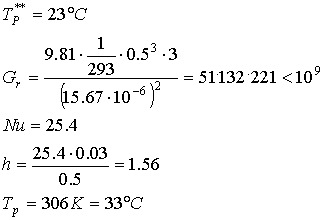
Nuovamente, il valore di secondo tentativo e quello uscito dai conti sono molto differenti per cui ne scelgo uno intermedio tra i due valori di tentativo
![]()
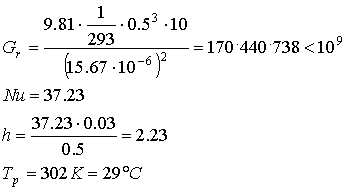
La temperatura finale di mattonella sarà una media tra i due valori
![]()
Vado allora a calcolare il coefficiente d'irragiamento alla luce del valore di temperatura della mattonella ora noto
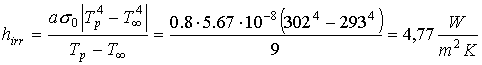
Il coefficiente d'irragiamento è il doppio rispetto al relativo coefficiente di convezione, il che indica il diverso peso dei contributi di potenza assorbita dalla piastrella.
![]()