Giulia Papotti, n° matr. 119047

25/10/99, ore 8:30/10:30

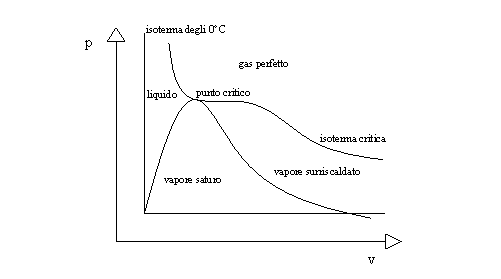
Nel diagramma pv (fig. 1) consideriamo solo la zona al di sopra dell'isoterma degli 0° centigradi. Per l'acqua è infatti la temperatura di solidificazione, e in questo studio lo stato solido non è di nostro interesse.

Al di sopra di tale isoterma si evidenziano quattro possibili stati fisici. Sono liquido, gas perfetto, vapore saturo, vapore surriscaldato distinti tra loro da isoterma critica e curva limite. 

Il nostro problema è calcolare date p pressione e T temperatura (indipendenti ovunque nel diagramma tranne che nella zona dei vapori saturi) le coordinate termodinamiche v volume specifico, u energia interna specifica, h entalpia specifica e s entropia specifica.

È lo stato in cui non si ha dipendenza del volume dalla pressione, ma solo dalla temperatura: v=v(T). Ciò equivale a considerare il liquido incomprimibile.

A causa di questa dipendenza nulla dalla pressione, nel diagramma pv le isoterme sono teoricamente verticali, con pendenza infinita con segno negativo. In pratica poi si hanno leggere deviazioni; ad esempio per l'acqua si ha una diminuzione di volume del 10% ad una pressione di 5000 bar: da ciò è evidente come tale variazione sia trascurabile lavorando a pressioni dell'ordine di quella atmosferica.

La dipendenza dalla temperatura di v e' tabulata, anche se più spesso e' data invece la densità che ne è il reciproco:

(1)

Dimensionalmente infatti la densità è misurata in kg/m³, v in m³/kg (è un volume riferito all'unità di massa).

Le due tabelle seguenti si riferiscono la prima all'acqua liquida alla pressione di 1 atm, la seconda al mercurio liquido a 0 °C.

Le altre proprietà, quindi u, h, s, si ricavano dal calore specifico. Per quanto riguarda questa quantità, si ha un'ulteriore semplificazione dato che c_p=c_v (siccome il liquido è incomprimibile e la pressione non ha effetto sul volume). È però in generale dipendente da T: c_p = c_v = c_L (T).

Per questo motivo se si lavora tra due stati 1 e 2 tra i quali c'è un grande salto di temperatura, si usa un calore specifico medio c_medio, ad esempio

(2)

Tale espressione del salto di energia interna è però formalmente uguale a quella del salto di entalpia:

(3)

È approssimativamente vero se il termine pv è trascurabile rispetto a h e u in:

(4)

Ci sono casi in cui però trascurare tale termine equivale a trascurare il fenomeno. Ad esempio in una pompa a centrifuga avendo in entrata p₁=1 bar, v₁=0,001 m³/kg, T₁=20 °C, e in uscita p₂=10 bar, v₂=0,001 m³/kg, T₂=20°C, si ha correttamente che u₂-u₁=0, in quanto il salto di temperatura è nullo.

Applicando la (3) si giungerebbe però ad un assurdo, cioè che anche la variazione di entalpia è nulla. Ma ciò non può essere poiché in netto contrasto con il principio di conservazione dell'energia: si avrebbe che il lavoro meccanico eseguito dalla pompa sarebbe sparito nel nulla. In questo caso quindi non si può trascurare il termine dato da pv. Quindi dovrò usare:

(5)

Questo perché u₂-u₁=0 e il volume e' costante. Possiamo cioè trascurare il termine pv solo se la variazione di temperatura non è infinitesima.

Calcoliamo ora l'entropia. Ricordiamo che in ogni caso si ha

(6)

Allora dalla definizione di entropia si ha che

(7)

Quindi integriamo tra gli stati 1 e 2. Essendo il calore specifico dipendente dalla temperatura, dovremo prenderne un valore medio tra T₁ e T₂:

(8)

Nella (8) le temperature sono espresse in Kelvin, non in centigradi, poiché ne compare il rapporto e non la differenza, e c_L è caratterizzato da un asterisco essendo calcolato mediante una media logaritmica, non con una media lineare come in (2).

Le medie lineare e la logaritmica sono così definite:

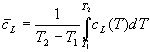(9)

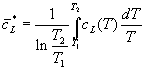(10)

Sono quindi in generale diverse poiché ottenute mediante costruzioni diverse.

Graficamente prendiamo in considerazione per il calcolo di (9) un diagramma c_LT (fig. 2). Allora il calore medio è l'altezza del segmento che moltiplicato per T₂-T₁ darebbe l'area sottesa dalla curva tra T₁ e T₂.

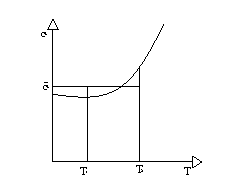
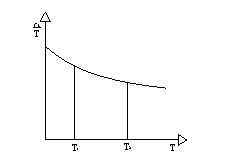
Per calcolare (10) invece dobbiamo considerare un diagramma dove c_L/T è funzione di T (fig. 3). Nel disegno ne è riportato un grafico ipotetico. In questo caso il calore medio è l'altezza del segmento che moltiplicato per il logaritmo naturale del rapporto tra le temperature, fornisce l'area sottesa dalla curva.

Talvolta però la differenza tra i due valori e' trascurabile: ad esempio per l'acqua c_L varia tra 4,16 e 4,20 kJ/kgK, quindi sostituendo ad entrambi 4,18 si commetterebbe un errore pienamente accettabile.

Spesso poi si calcola la media aritmetica che è molto più semplice:

(11)

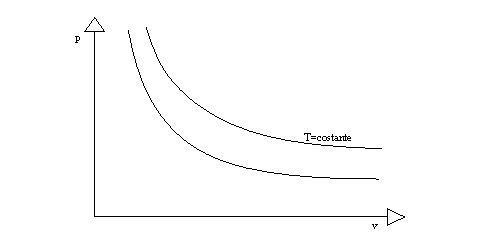
Nel diagramma pv siamo a pressioni e temperature abbastanza alte da essere lontani dalla curva critica e in modo da avere le isoterme rappresentate con iperboli equilatere (fig. 4). Vale infatti l'equazione di stato dei gas perfetti:

(12)

in cui p è la pressione in Pascal, v il volume specifico in m³/kg, T la temperatura espressa in gradi Kelvin. R è la costante del gas perfetto che dipende dal gas in esame e si ricava dividendo la costante universale R₀ per la massa molare della sostanza considerata:

(13)

Si ha ad esempio che per l'aria R_aria=287 J/kgK. Infatti la sua massa molare si ricava combinando linearmente le masse molari di ossigeno e azoto nelle proporzioni che la costituiscono (circa un quarto di ossigeno e tre quarti di azoto), e si ha che m_oss=32 kg/kmol e m_azoto=28 kg/kmol. Quindi:

(14)

Per l'acqua invece m_acqua=18 kg/kmol, da cui R=462 J/kgK.

Dalla (12) ricaviamo direttamente il volume specifico dividendo entrambi i membri per p:

(15)

Per il gas perfetto si dimostra anche che:

(16)

Ad esempio per l'aria si ha che c_p=1004 J/kgK, da cui

(17)

Inoltre si ha un'altra relazione che definisce g come:

(18)

Tale g è un numero puro e vale g₁=1,57 per i gas monoatomici e g₂=1,41 per i biatomici (per esempio N₂ o O₂). Sarà utilizzato come esponente di v nell'espressione che descrive le trasformazioni isoentropiche (in cui cioè s=const):

(19)

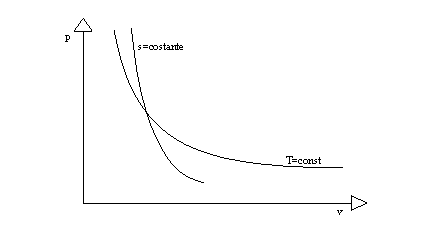
In figura 5 è confrontato l'andamento di una isoterma con quello di una isoentropica.

Le (16) e (18) sono due equazioni che permettono di trovare c_p e c_v, non rendendo quindi necessarie tabelle che ne rechino i valori tabulati.

Per ricavare le altre coordinate termodinamiche utilizziamo il primo principio della termodinamica in forma differenziale:

(20)

Siccome l'energia interna è una variabile di stato dipende solo dai valori iniziale e finale, non dal percorso seguito. Allora per muoverci dallo stato 1 allo stato 2, tra i quali si ha sia variazione di v sia di T, scegliamo per semplicità un'isoterma e una trasformazione a volume costante. Dal punto 1 scendiamo verticalmente sino ad incontrare l'isoterma di 2 nel punto C, isoterma che poi seguiamo per arrivare fino al punto 2 (fig. 6).

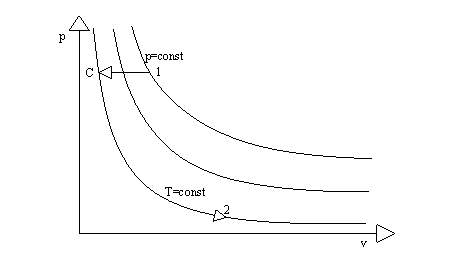
Dalla legge di Joule abbiamo che sia l'energia interna sia l'entalpia dipendono dalla temperatura, ma non da p o v. Allora la variazione di energia interna si avrà solo tra 1 e C, e essendo tale trasformazione caratterizzata da v=const, si ha che pdv=0, e quindi:

(21)

e siccome per i gas perfetti si assume che c_v non dipenda dalla temperatura

(22)

Ancora dal primo principio:

(23)

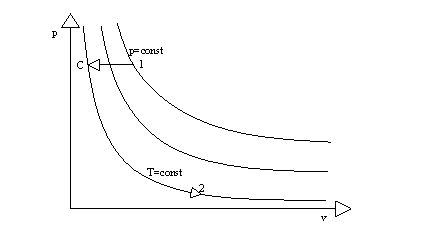
Stavolta seguiamo un'isoterma e una trasformazione a p costante (fig. 7). Lungo l'isoterma T=const per definizione, e quindi, ancora dalla legge di Joule, non si ha variazione di entalpia. Tale variazione allora è solo sul tratto 1C, in cui essendo p=const, vdp =0. Allora:

(24)

e quindi integrando tra gli istanti 1 e 2:

(25)

Possiamo poi scegliere arbitrariamente la temperatura di 0 gradi centigradi come riferimento, e quindi porre u₀=0 e h₀=0, così da avere le espressioni di energia interna e entalpia assolute (in cui t è la temperatura in gradi centigradi):

(26)

Con questa scelta quindi, possono esistere anche entalpie negative (nel caso in cui lo sia t). Ad esempio per l'aria abbiamo che c_p =1 kJ/kgK, alla temperatura di t₁=100°C sarà h₁=100000 J/kg, mentre per t₂= -20°C h₂= -20000 J/kg.

Per quanto riguarda il calcolo dell'entropia specifica del gas perfetto possiamo seguire due strade partendo da due diverse formulazioni del primo principio.

Dalla forma infinitesimale, cioè la (20), si ha, sostituendo la (21):

(27)

Allora dalla definizione di entropia:

(28)

Ma ricordando l'equazione (12), si ottiene p/T=R/v che sostituito in (28):

(29)

Integriamo quindi gli stati 1 e 2:

(30)

Similmente si procede partendo dalla forma entalpica del primo principio, (23), sostituendo la (24):

(31)

Ancora dalla definizione di entropia:

(32)

Ma dalla (12) si ha che v/T=R/p, che sostituita in (32):

(33)

Integrando sempre tra gli stati 1 e 2:

(34)

Le (30) e (34) sono equivalenti tra loro, anche se spesso è più usata la (34) in quanto di solito sono date le coordinate pT, non vT.

Utilizzando ancora la (12) si può ottenere anche una terza formulazione, l'entropia in funzione della coppia pv, considerando il fatto che T=pv/R:

(35)

Grazie alle proprietà dei logaritmi tale espressione può essere ulteriormente semplificata (utilizzando anche la (16)):

(36)

Nel caso di una trasformazione isoentropica, si ha evidentemente che s₂-s₁=0, allora utilizzando ancora le proprietà dei logaritmi nella (36), si ha:

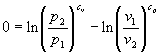(37)

L'uguaglianza dei logaritmi impone l'uguaglianza degli argomenti degli stessi:

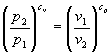(38)

Allora estraendo la radice "c_v-esima":

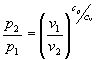(39)

(40)

Utilizzando la (18) si ottiene esattamente la (19) che quindi come anticipato prima descrive una trasformazione isoentropica.

Sono di seguito tabulati i valori del gas aria a pressione atmosferica.

Per questo stato manca una teoria generale compiuta come quelle già viste per liquido e vapore. Per il suo studio ci si appoggia appunto a tali due stati e si utilizza la grandezza x, detta titolo, definita come:

(41)

Il titolo è un numero puro, compreso tra 0 e 1, in particolare a x=0 corrisponde lo stato di liquido (L in figura 8), a x=1 lo stato vapore V.

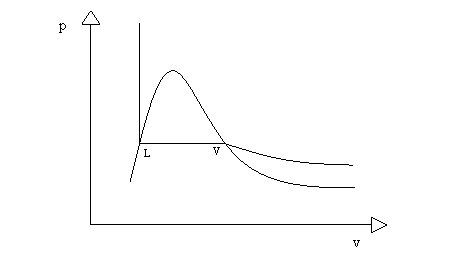
Abbiamo infatti che le generiche proprietà (v, u, h, s) sono date per liquido e vapore, e che la corrispondente proprietà del vapore saturo è data dall'interpolazione lineare di quelle due.

Nelle tabelle che riportano i valori di tali proprietà, ad esempio dell'energia interna, spesso è riportata invece della coppia (u_l u_v), la coppia (u_l u_d), dove u_d è l'energia interna differenziale, definita come:

(42)

Quindi l'energia interna del vapore è funzione lineare di x titolo secondo la relazione:

(43)

che è evidentemente verificata sostituendo la definizione (42).

Sono identicamente definite le altre coordinate:

(44)

(45)

(46)

Effettivamente poi in alcune tabelle riguardanti i vapori saturi troviamo solo alcuni di questi valori e cioè (p, T, h_d). Infatti i valori dello stato liquido sono già riportati nelle tabelle dello stesso. L'energia interna differenziale e l'entropia interna differenziale sono calcolabili dalle

(47)

(48)

Da notare anche il fatto che h_d entalpia differenziale è detta anche calore latente di vaporizzazione r, e questo per motivi storici (risalenti a quando era ancora utilizzato il calorico).

In tabella sono riportati i valori del vapor d'acqua saturo.