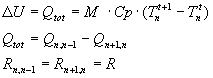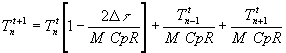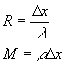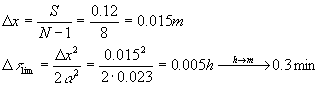FRANCESCO NAPOLI mat.128340 Lezione del 10\01\2000 ore 16:30\18:30
SCAMBIO TERMICO IN REGIME TRANSITORICO
Lo scambio termico in regime transitorico viene effettuato mediante l’equazione di Fourier :
![]()
![]()
![]()
La soluzione di questa equazione può essere fatta mediante un calcolo di scomposizione in serie di funzioni ma il processo è lungo e molto difficoltoso. Si preferisce in questi casi applicare la soluzione numerica.
Il calcolo numerico dell’equazione sopra descritta viene fatto utilizzando due metodi, dei quali faremo riferimento solo al primo:
1-Metodo alle differenze finite;
2-Metodo agli elementi finiti;
La soluzione alle differenze finite è molto semplice, abbastanza precisa e, inoltre, può essere facilmente riproposta su calcolatore tramite un banale foglio di calcolo ( excel ad esempio).
Tale metodo è basato sulla discretizzazione geometrica del problema mediante suddivisione finita in celle (linee,superfici o volumi ) delle quali si considerano le singole proprietà, che rappresentano le variabili da trovare.
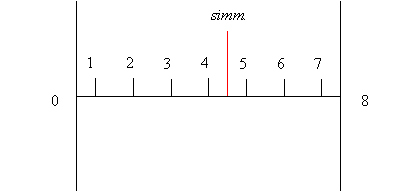
Studiamo come esempio il caso di una lastra piana inizialmente a temperatura
To:
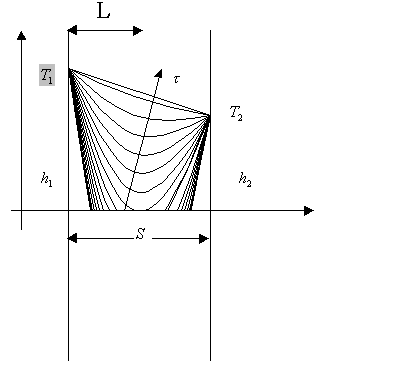
In figura sono illustrate le curve che rappresentano l’andamento della temperatura dopo che, all’istante t=0, la lastra viene immersa in un liquido con temperatura T ![]() To. La parete di contatto raggiunge la nuova temperatura T, e ciò avviene istantaneamente se h1 e h2 ( rispettivamente coefficiente di convezione del fluido e coefficiente di convezione dell’ambiente esterno) sono tendenzialmente infiniti. Per verificare la veridicità dell’ipotesi sfruttiamo il numero di Biot
To. La parete di contatto raggiunge la nuova temperatura T, e ciò avviene istantaneamente se h1 e h2 ( rispettivamente coefficiente di convezione del fluido e coefficiente di convezione dell’ambiente esterno) sono tendenzialmente infiniti. Per verificare la veridicità dell’ipotesi sfruttiamo il numero di Biot
![]()
dove:
h = coefficiente di convezione
L = lunghezza relativa
l
= coefficiente di convezione(per questo caso L=S/2)
In base al valore del numero di Biot possiamo considerare h nel seguente modo:
![]()
L’ipotesi è valida quindi nel caso in cui il numero di Biot sia maggiore di 40, nell’altro caso non solo l’ipotesi non è accettabile ma il materiale tende a mantenere la sua temperatura costante evidenziando l’indipendenza dal parametro spaziale x.
Supponiamo per i nostri scopi l’ipotesi di B>40 accettabile. Procediamo nel seguente modo:
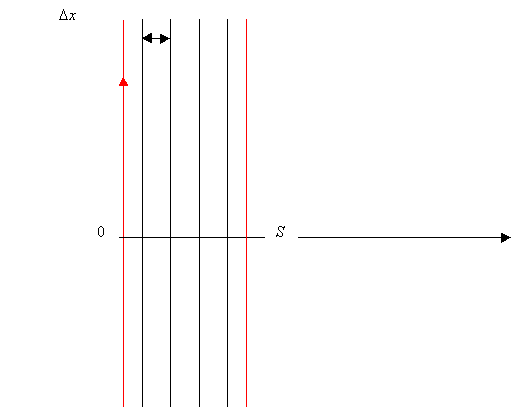
Si suddivide la lastra in un numero fissato di nodi N. Ad ogni nodo si fa corrispondere uno spessore Dx fissato al valore
![]()
tranne al primo ed ultimo nodo il cui valore di Dx è pari alla metà del valore nominale.
N rappresenta il numero di passi, Dx è il passo spaziale.
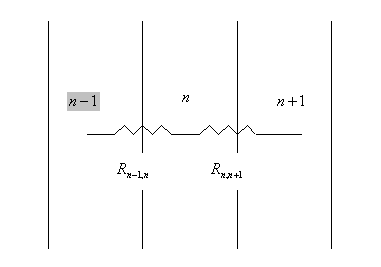
In modo analogo si procede alla discretizzazione del tempo in N nodi e Dt=t/(n-1) passi temporali ed alla discretizzazione di altre eventuali variabili. Si passa quindi a risolvere la rete elettrica equivalente:
![]()
![]()