Esercizi d’esame
ESERCIZIO 1
[ 15/10/99 n° 2 – Fluidodinamica (tolleranza +/- 10%)]
Davide Mezzadri - matr. 117630 - Lezione del 23/11/99 - ora 14:30-16:30
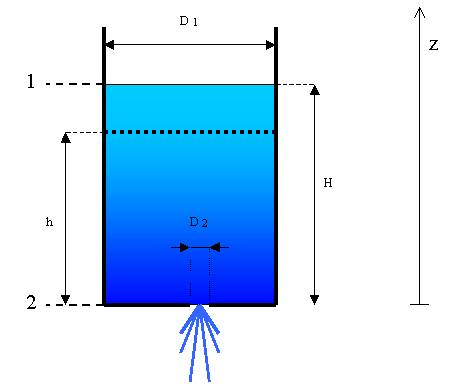
Un serbatoio di forma cilindrica ha un diametro di 1+0.01*BC m e contiene acqua sino ad un livello di 10+D m. Sul fondo di esso viene aperto un foro circolare con bordi smussati (b = 0.5), con diametro pari ad 1/20 di quello del serbatoio, per cui l’acqua comincia ad uscire. Determinare il tempo necessario al completo svuotamento del serbatoio.
Tempo di svuotamento t = ? [ s]
Disegno :

Dati :
Matricola :
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
2
|
3
|
4
|
5
|
6
|
D1 = 1+0.01*BC = 1.23 m
H = 10+D = 14 m
D2 = (1/20)D1 = 0.0615 m
b = 0.5
Scelta delle sezioni :
- sezione1 al pelo libero ;
- sezione2 allo sbocco .
SOLUZIONE :
Il quesito da risolvere è il classico problema dello svuotamento di un serbatoio.
Le condizioni del sistema variano continuamente :
L’equazione generale di bilancio dell’energia di un sistema aperto è :
![]() (1)
(1)
Applico questa equazione al nostro sistema tenendo presente le seguenti considerazioni :
E quindi :
![]() (2)
(2)
L’equazione ricavata ha apparentemente incognite le due velocità W2 e W1 , ma grazie all’equazione di continuità riesco ad esprimere W2 in funzione di W1 :
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
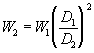 (6)
(6)
![]() (7)
(7)
Sostituisco il valore ricavato nel bilancio energetico e ottengo :
![]() (8)
(8)
La velocità può essere espressa come derivata della variazione di altezza nel tempo :
![]() (9)
(9)
Il segno meno indica che la variazione di altezza è negativa , cioè contraria all’asse di riferimento z .
Raccolgo a fattore comune la velocità :
![]() (10)
(10)
Uguaglio le due equazioni della velocità :
![]() (11)
(11)
Ottengo un’equazione differenziale di 1° grado a variabili separabili :
![]() (12)
(12)
Integro :
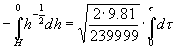 (13)
(13)
Poiché la risoluzione generale dell’ integrale al primo membro è :
![]() (14)
(14)
Otteniamo :
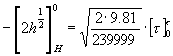 (15)
(15)
![]() (16)
(16)
Sostituendo i valori numerici troviamo la soluzione al problema :
![]() (17)
(17)
Commento :
Il testo del problema ci fornisce tra gli altri dati quello del diametro del serbatoio che però non viene utilizzato ; infatti il valore fondamentale per la risoluzione dell’esercizio è il rapporto dei due diametri (quello del serbatoio e quello allo sbocco) .
La tolleranza fornita è in questo caso inutile perché nella risoluzione dell’esercizio non abbiamo fatto ricorso ad interpolazioni tra dati o altro .
ESERCIZIO 2
[ 9/9/99 n° 2 – Fluidodinamica (tolleranza +/- 5%)]
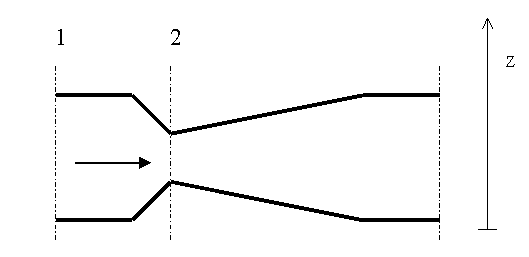
Per misurare la portata d’acqua che scorre in una tubazione , sulla stessa è inserito un tubo di venturi. Il diametro della tubazione è di D1 =50+BC mm , il diametro della gola del venturi è D2 =30+D mm . Si misura una differenza di pressione pari a 10000+BCDEF Pa . Determinare velocità e portata nel condotto.
Disegno :
Dati :
Matricola :
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
2
|
3
|
4
|
5
|
6
|
D1= 50+BC = 50+23 = 73 mm
D2= 30+D = 30+4 =34 mm
P1 – P2 = 10000+BCDEF = 33456 Pa
r acqua = 1000 Kg/m3 (valore riportato da tabella)
Scelta delle sezioni :
- sezione1 nella tubazione (diametro = D1 ) , prima della gola ;
- sezione 2 nella gola del venturi (diametro = D2 ) .
SOLUZIONE :
L’equazione generale di bilancio dell’energia di un sistema aperto è :
![]() (18)
(18)
Applico questa equazione al nostro sistema tenendo presente le seguenti considerazioni :
E quindi :
![]() (19)
(19)
Le velocità sono entrambe incognite ma dato che sono legate dall’equazione di continuità , e ipotizzando r costante , otteniamo :
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
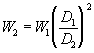 (23)
(23)
Si sostituisce nell’espressione di partenza :
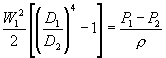 (24)
(24)
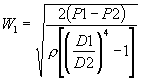 (25)
(25)
A questo punto inserendo i valori numerici si ha :
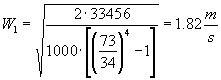 (26)
(26)
Infine si calcola la portata nel condotto :
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
ESERCIZIO 3
[ 22/7/99 n° 2 – Fluidodinamica (tolleranza +/- 10%)]
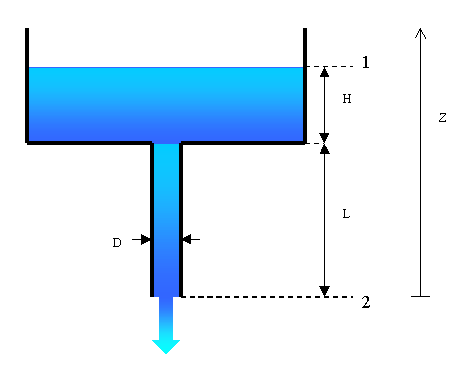
Un serbatoio d’acqua di grande capacità alimenta un condotto verticale lungo 10+F metri , avente un diametro idraulico pari a 70+DE mm . L’altezza del pelo libero dentro il serbatoio è 4+C metri dal fondo . Considerando il tubo liscio , determinare velocità media e portata dell’acqua fuoriuscente dal condotto .
Disegno :
Dati :
Matricola :
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
2
|
3
|
4
|
5
|
6
|
L = 10+F = 10+6 = 16 m
D = 70+DE = 70+45 =115 mm
H = 4+C = 7 m
e = 0 (ovvero tubi lisci)
b = 1 (a causa dell’imbocco)
Scelta delle sezioni :
SOLUZIONE :
L’equazione generale di bilancio dell’energia di un sistema aperto è :
![]() (30)
(30)
Applico questa equazione al nostro sistema tenendo presente le seguenti considerazioni :
![]() (31)
(31)
![]() (32)
(32)
Da cui si ricava il valore della velocità :
![]() (33)
(33)
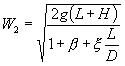 (34)
(34)
Il fattore di attrito x dipende dal numero di Reynolds che a sua volta dipende dalla velocità incognita ; quidi per procedere nella soluzione del problema si deve utilizzare una velocità di primo tentativo. La scelta di questa velocità viene effetuata imponendo un tetto massimo agli ipotetici valori mediante la velocità torricelliana :
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
Una velocità di 21.2 m/s per un’altezza di 23 m è sicuramente un valore troppo elevato ; per questo si può decidere di prendere una velocità dello stesso ordine di grandezza , ma inferiore ad esempio :
![]() (38)
(38)
Mediante la velocità di primo tentativo si calcola il numero di Reynolds :
![]() (39)
(39)
Ricordando che la scabrezza e è nulla e sapendo che il numero di Reynolds identifica una regione di moto turbolento , ricaviamo dal diagramma di Moody il valore del fattore di attrito .
Il risultato grafico è x 1 = 0.012 ; inseriamo quest’ultimo nell’equazione che fornisce la velocità e otteniamo :
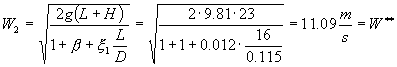 (40)
(40)
Il valore che avevamo ipotizzato era quindi troppo piccolo. Proseguiamo ora ricorsivamente fino a che il valore di velocità si discosta da quello precedentemente calcolato di una quantità inferiore alla tolleranza richiesta :
![]() (41)
(41)
Otteniamo dal grafico x 2 = 0.010 ; allora :
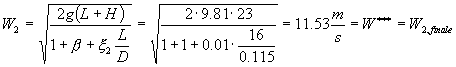 (42)
(42)
W* = 7.00 m/s -- Re’ = 805000 -- x 1 = 0.012 -- W** = 11.09 m/s
W**= 11.09 m/s -- Re’’ = 1275350 -- x 2 = 0.010 -- W*** = 11.53 m/s
Una volta trovata la velocità dell’acqua fuoriscente dal condotto , si ricava la portata:
![]() (43)
(43)
Commento :
Il meccanismo di calcolo ricorsivo funziona sempre perché le curve di Moody sono monotone decrescenti . La soluzione è però leggermente imperfetta in precisione a causa della ricerca grafica dei valori desiderati .
ESERCIZIO 4
[ 19/2/99 n° 2 – Fluidodinamica ]
Trovare la velocità di caduta libera , in aria , di un corpo di forma sferica.
Diametro della sfera D = 0.001+0.001*F [ m]
Densità della sfera r s = 500+10*EF [ Kg/m3]
Temperatura dell’aria T = 0.5*CD [ °C]
- Coeff. di resistenza CR = ?
- Velocità di caduta u = ? [ m/s]
Disegno :
Dati :
Matricola :
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
2
|
3
|
4
|
5
|
6
|
D = 0.001+0.001*F= 0.001+0.006 = 0.007 m
r s = 500+10*EF = 500+560 = 1060 Kg/m3
T = 0.5*CD = 0.5*34 = 17°C
u aria = 15.7*10-6 m2/s (dato tabulato relativo all’aria in funzione della temperatura)
SOLUZIONE :
Il parametro incognito richiesto dall’esercizio è la velocità a cui si stabilizza la sfera in caduta libera . Su di essa agiscono due forze : il peso della sfera applicata nel suo baricentro che agisce verso il basso , e la forza di attrito viscoso che agisce verso l’alto :
![]() (44)
(44)
![]() (45)
(45)
La sfera cade di moto accelerato non uniforme : mentre la forza peso è costante , la reazione dell’aria è funzione quadratica della velocità di caduta ,quindi è molto variabile . Il corpo raggiungerà la sua velocità limite quando le due forze saranno esattamente equilibrate , cioè quando la resistenza dell’aria avrà uguagliato il peso della goccia. Uguagliando le due forze si trova la condizione di equilibrio :
![]() (46)
(46)
Possiamo esplicitare direttamente il valore della velocità di caduta, ricordando i valori di volume e di area frontale per una sfera :
![]() (47)
(47)
![]() (48)
(48)
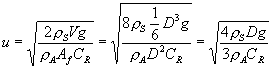 (49)
(49)
Osserviamo dunque che la velocità di caduta cresce con la radice quadrata del diametro , quindi non linearmente , ma nonostante ciò un corpo grosso (ad esempio i goccioloni di pioggia dei temporali estivi) cade più velocemente di uno piccolo( ad esempio la pioggia leggera primaverile) .
Calcolo la densità dell’aria sfruttando l’equazione dei gas perfetti :
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
Il numero di Reynolds è per definizione :
![]() (53)
(53)
Nell’equazione( ) la velocità incognita per essere ricavata richiederebbe già la conoscenza di CR che dipende dal numero di Reynolds e quindi dalla velocità stessa .
Dobbiamo prendere una velocità di primo tentativo per entrare una prima volta nel diagramma che mi fornisce il coefficiente CR in funzione del numero d Reynolds . In questo caso non abbiamo un tetto massimo dei valori di prova , come la velocità torricelliana , e quindi "batteziamo" , secondo il nostro buon senso , una velocità di primo tentativo u0 = 10 m/s :
![]() (54)
(54)
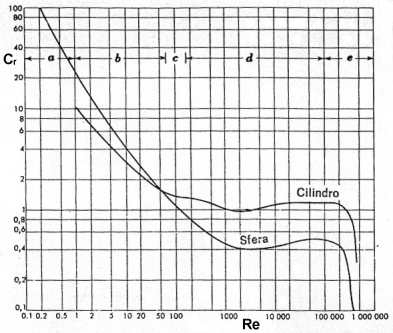
(Grafico 1)
Ricavo un valore di CR0 = 0.40
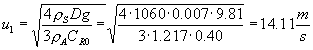 (55)
(55)
Si procede ricorsivamente fino a che il valore di velocità si discosta da quello precedentemente calcolato di una quantità inferiore alla tolleranza richiesta :
u0 = 10.00 m/s -- Re0 = 4458.59 -- CR0 = 0.40 -- u1 = 14.11 m/s
u1 = 14.11 m/s -- Re1 = 6291.08 -- CR1 = 0.42 -- u2 = 13.79 m/s
u2 = 13.79 m/s -- Re2 = 6149.41 -- CR2 = 0.41 -- u3 = 13.97 m/s
Commento:
Il grafico del coefficiente CR in funzione del numero di Reynolds , per una sfera, ha un zona abbastanza piatta e quindi può fornire uguali valori di CR per diversi numeri di Reynolds ; questo implica il rischio di potersi mettere ad oscillare prima di trovare la soluzione . Il calcolo risulta essere leggermente impreciso a causa di una interpolazione grafica nella lettura dei dati.
ESERCIZIO 5
[ 15/4/99 n° 2 – Fluidodinamica ]
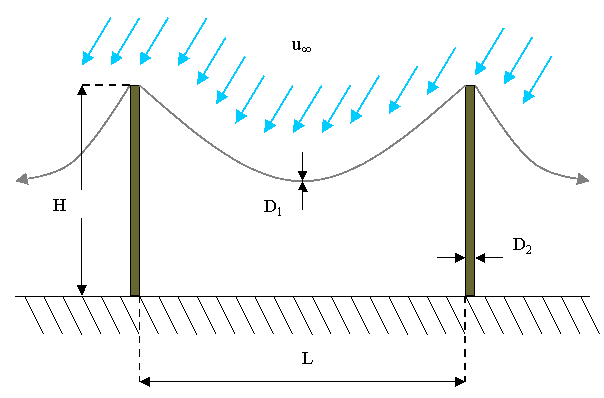
Trovare lo sforzo risultante esercitato dal vento alla base dei pali di una linea telefonica, nell’ipotesi che lo stesso soffi in direzione ortogonale alla linea . I pali sono alti 10 m e distano l’uno dall’altro 50 m , e la velocità del vento è di 20 m/s.
Diametro del cavo telefonico D1 = 0.003+0.001*F [ m]
Diametro del palo di sostegno D2 = 0.1+E*0.01 [ m]
Temperatura dell’aria T = 0.5*CD [ °C]
- Forza applicata dal filo al palo FFilo = ?[ N]
- Forza complessiva alla base del palo FTOT = ? [ N]
Disegno :
Dati :
Matricola :
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
2
|
3
|
4
|
5
|
6
|
D1 = 0.003+0.001*F = 0.009 m
D2 = 0.1+E*0.01 = 0.15 m
T = 0.5*CD = 17 °C
u¥ = 20 m/s
L = 50 m
H = 10 m
r Aria = 1.27 Kg/m3 (valore ricavato nell’equazione 52)
u Aria =15.7*10-6 m2/s (dato tabulato relativo all’aria in funzione della temperatura)
SOLUZIONE :
Lo sforzo totale alla base di un palo è dato da tre contributi :
Se consideriamo ogni singolo palo notiamo che questo deve poter sopportare una forza dovuta ad una quantità di filo L (L/2 a detra e L/2 a sinistra).
In generale la forza di trascinamento è così definita :
![]() (56)
(56)
Si applica queta relazione ad un tratto di filo lungo L (L/2 a destra + L/2 a sinistra) e che ha quindi un’area frontale Af = LD1 ; allora :
![]() (57)
(57)
Si applica queta relazione al palo di altezza H e che ha quindi un’area frontale Af = HD2 ; allora :
![]() (58)
(58)
Calcoliamo i rispettivi numeri di Reynolds :
![]() (59)
(59)
![]() (60)
(60)
Questi ultimi valori ci permettono di trovare via grafica (grafico 1) i rispettivi coefficienti : CR,Filo = 1.3 e CR,Palo = 1.05 .
Calcoliamo quindi le due forze :
![]() (61)
(61)
![]() (62)
(62)
La forza totale è :
![]() N (63)
N (63)
Commento :
Se il quesito fosse stato quello di trovare la forza totale ,non alla base del palo , ma ad esempio a metà del palo stesso avrei dovuto considerare ,oltre alla forza del filo , la forza agente su un’altezza H/2 del palo .
![]()
![]()