Propagazione in Ambiente Esterno

In questa lezione si è cercato di fissare la teoria per la propagazione del suono in ambiente esterni. Gli esempi che si possono fare su sistemi interessati da queste speculazioni sono molteplici:

• rumore prodotto da mezzi di trasporto (auto, treni, aeroplani)
• edifici (sistemi di refrigerazione, ventilatori)
• sistema di amplificazione per esterni (per concerti in uno Stadio)

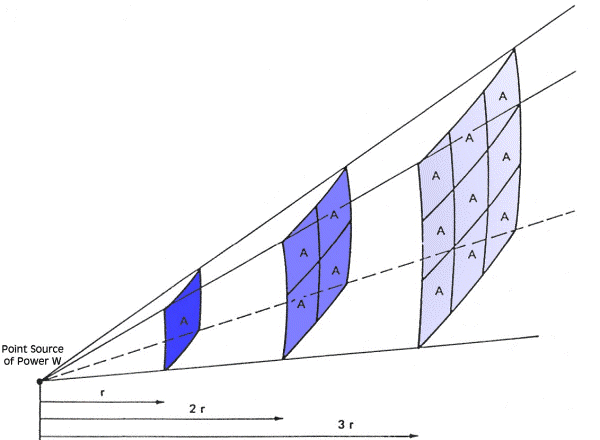
La propagazione sferica è facile da descrivere: una sorgente piccola rispetto alla lunghezza d’onda e il ricevitore lontano dal centro. In queste condizioni P e v calano con l’aumentare della distanza che è il raggio della propagazione.

Decadimento con la distanza

L’energia che si propaga resta in prima approssimazione costante (nessun assorbimento da parte dell’aria) ma la densità sonora diminuisce perché si distribuisce su una superficie sempre più grande.

Sia L_db=80dB l’intensità a 1m, L_db a 2m vale . La diminuzione di intensità al raddoppio della distanza ha una sigla (DL2) e nel caso della propagazione sferica vale sempre DL2=6dB ed è il livello massimo che si può ottenere da una qualsiasi propagazione.
 

(1)
(2)	(4)
(3)	(5)

 

Sono tutti livelli espressi in decibel. Solo L_W non è omogenea alle altre (il livello di potenza dipende dalla sorgente e di conseguenza L_W resta costante in ogni punto)

Fissato dunque L_W, possiamo dedurre il livello di intensità:

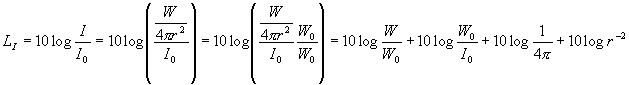
Essendo i valori di riferimento W₀ e I₀ arbitrari li possiamo scegliere uguali al fine di semplificare la relazione e i loro valori effettivi (valori che saranno spiegati in seguito) sono:

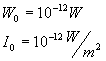e dalle altre relazioni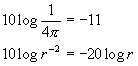 

Possiamo ricavare la (2) dalla (1): 

Determinato questo valore vogliamo che le altre relazioni (3) (4) e (5) assumano in un dato punto lo stesso valore che assume L_I per poter così parlare di unico Livello Sonoro, e ciò è sempre possibile visto che i valori di riferimento sono arbitrari.
 
 

Conosciamo anche una relazione che unisce la velocità alla pressione (solamente nelle onde piane progressive o in onde sferiche)  .

Se prendiamo un valore particolare della  il valore di u₀ resta fissato e vale .

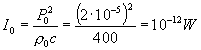abbiamo così ottenuto il valore di I₀ precedentemente usato (che è anche uguale a W₀).

In queste condizioni è facile da verificare che .

Ovviamente fuori dal caso di onda piana progressiva le relazioni vengono meno. E’ già stato verificato che in un tubo * i valori p e v si alternano. Non è solo il caso del tubo, ma semplicemente in ogni stanza reale, dove i valori di I, D, P, u, sono leggermente diversi in ogni punto. Una grandezza comunque è limitata : , la prima è l’energia che si propaga (e interferisce con l’energia riflessa), mentre la seconda è un’energia vera e propria, e dunque somma sia dell’energia che si propaga e dell’energia riflessa.

Possiamo dunque utilizzare questa differenza  per stimare la propagazione teorica di un suono in un ambiente.

Se questa differenza è inferiore 1 dB l’ambiente chiuso si dice anecoico, ed è ottenuto solamente in stanze, dette appunto anecoiche, dove le pareti presentano una particolare geometria: esse sono coperte di elementi, chiamati wedge, che disperdono il suono e riducono la riflessione.

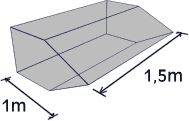
Figura 1 Wedge

Ricordiamo che le grandezze sono omogenee e solo in prima approssimazione rappresentano l’energia. In un ambiente minimamente riflettente, ogni grandezza ha una storia a parte.

In un tubo ad onde stazionarie per esempio non possiamo legare mai L_I per esempio a L_P.

[IMG]

varia da punto a punto, mentre  dipende dal terminatore a .

La norma ISO9614 è da considerarsi in questo senso obsoleta in quanto usa come metro di campione proprio la differenza  invece che la più corretta .

Temperatura dell’aria

La temperatura dell’aria è variabile con la quota. Di tutte le possibili configurazioni di questa variazione se ne possono sintetizzare tre dei possibili casi:

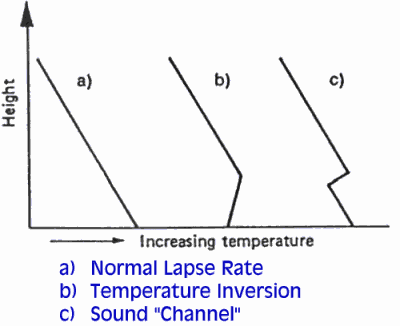
In queste diverse condizioni il fronte sonoro non si propaga linearmente ma tende a incurvari.

Per i disegno è stato adottato il metodo delle linee di campo sonoro (raggi sonori o Sound Rays): questi raggi sono ortogonali al fronte d’onda e rappresentano punti di iso intensità sonora.
 

a) Andamento Normale
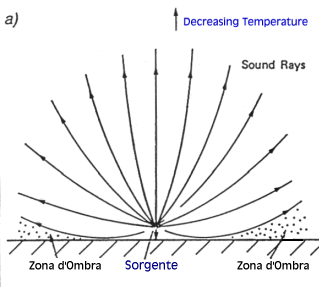	La temperatura diminuisce con l’allontanarsi dal terreno. I raggi sonori si aprono e si dirigono verso l’alto. Esiste una superficie (teorica) limite, tangente al terreno, sotto la quale il suono non arriva e si presenta una zona d’ombra sonora.
b) Inversione Termica
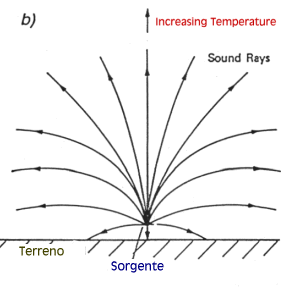	E’ una delle configurazioni tipica della Pianura Padana: il terreno è più freddo dell’aria circostante, fino a quando l’altezza non comincia a prevalere.
c) Canale Sonoro
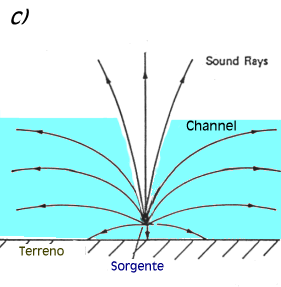	E’ un fenomeno che si presenta normalmente in presenza della nebbia. Il terreno è caldo, ma la nebbia è più fredda e la temperatura scende. Appena si supera la coltre, il sole riscalda l’aria e la temperatura aumenta, fino a quando torna a prevalere la diminuzione di temperatura con l’altezza. Il suono sale e viene intrappolato in un canale formato dalla nebbia stessa e in queste condizioni il suono percorre distanze notevoli (rispetto ai casi precedenti) prima di ricadere a terreno.

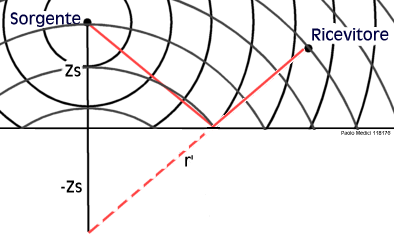
Interazione con una superficie orizzontale

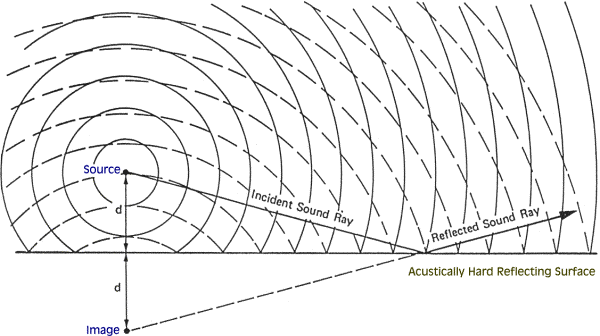
Se la sorgente è non coerente (per esempio di tipo random) anche il suono riflesso è random e la risultante in un punto è ancora un segnale indipendente dalla sorgente.
 
 

• piano perfettamente riflettente

Suono Diretto	Suono riflesso

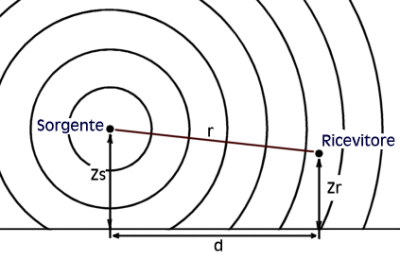
E’ immediato constatare che  pertanto il riflesso è un suono più basso del diretto, e arriva dopo.

Se il suono fosse random e sufficientemente sfasate l’intensità risultante sarebbe la somma dei due contributi.
 
 

• piano riflettente con coeficiene di assorbimento a

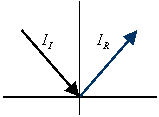
. Se a =0 la superficie è speculare e si torna al caso precedente.

Nei casi di superfici non speculare entrano anche le superfici che non solo assorbono parte l’onda, ma che tendono anche a diffonderla.

Sorgente Sonora Lineare

Consideriamo adesso il caso di una sorgente sonora non più puntiforme, ma lineare. I fronti d’onda adesso non sono più sferici, ma cilindrici.

Questo argomentazione permette la trattazzione di strade, ferrovie, linee di trasporto in generale, visto che si propagano in modo lineare.
 
 

Al fine del calcolo del livello equivalente obbliga a scomporre un singolo evento in una serie di piccoli, ma continui eventi.

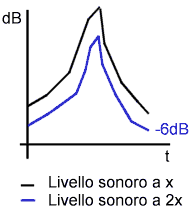
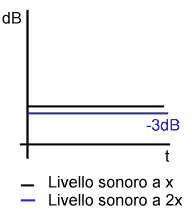
I due segnali sono però profondamente differenti: se raddoppio la distanza dal primo il livello scende di 6dB, se mi allontano dal secondo solo di 3dB:

dove con s ho indicato la densità di energia (energia prodotta da 1 m)

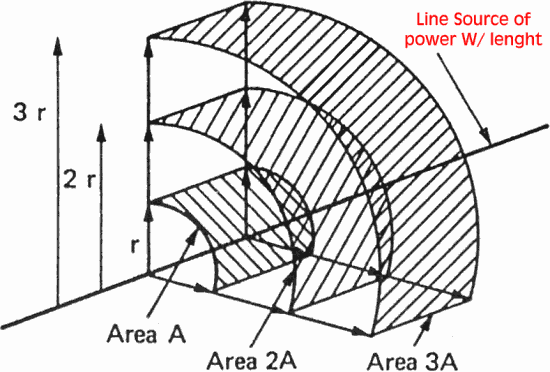
DL2=3dB
 
 

Se mi allontano da un’autostrada (sorgente lineare) il livello sonoro scende di 3dB/raddoppio, mentre se mi allontano da una fabbrica (sorgente concentrata) il livello sonoro cala di 6dB/raddoppio della distanza.
 
 

Effetti diffrattivi

Le onde sonore, come le onde elettromagnetiche, interagiscono con la materia, ma a differenza di queste ultime si ha un comportamento diverso se analizzate a bassa o alta frequenza. Questo comportamento è conseguenza del fatto che nel caso delle onde elettromagnetiche le fenditure sono un migliaio di volte maggiori della lunghezza d’onda incidente, mentre in questo caso, dove le grandezze in gioco hanno pressappoco la stessa dimensione, ci possono essere risposte diverse a seconda delle diverse lunghezze d’onda.
 

	Bassa frequenza	Alta Frequenza
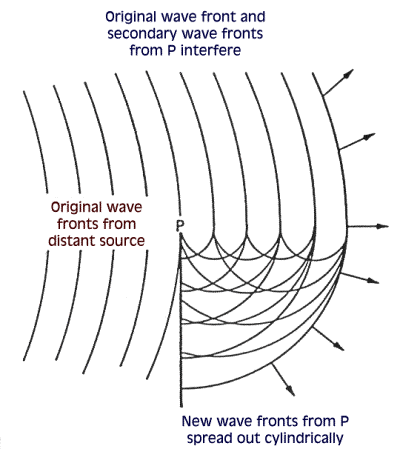
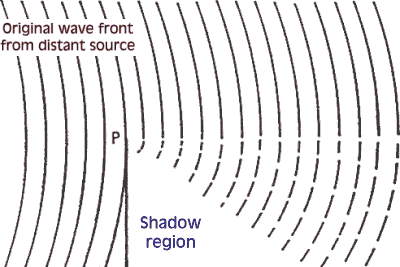
Ostacolo (un muro che si propaga perpendicolare al foglio)	Il bordo esterno P diventa esso stesso sorgente di un’onda cilindrica	L’onda cilindrica non è completa, con la formazione di una zona d’ombra.
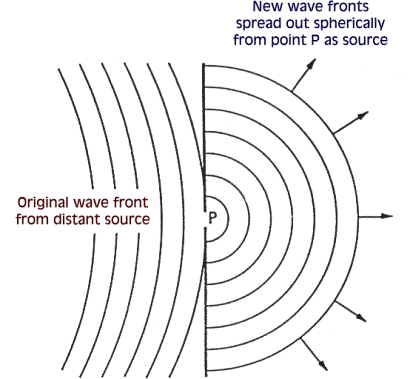
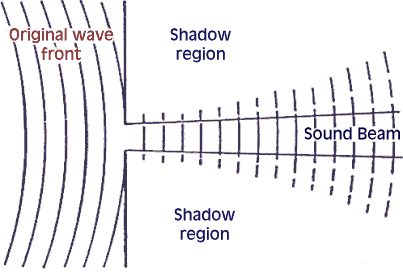
Fenditura	La fenditura è sorgente di un’onda sferica	Si forma un raggio, il quale è più collimato più è alta la frequenza.

 

Curve di Maekawa

Avevano ricavato che in campo libero i livello sonoro decresce con la formula . Se tra la sorgente e il ricevitore poniamo un ostacolo, come cambia questo valore? L’ostacolo è uno schermo di altezza definita, sufficientemente spesso per evitare la propagazione attraverso la parte solida, e invece molto lungo. Un muro è un esempio. In questa condizione, a parità di dimensioni, si ottiene (per via sperimentale) che il materiale di cui è costituito il muro non influenza il decadimento.
 
 

Maekawa per via teorica propose questa relazione:

e  dove N è un numero puro detto di Fresnel:

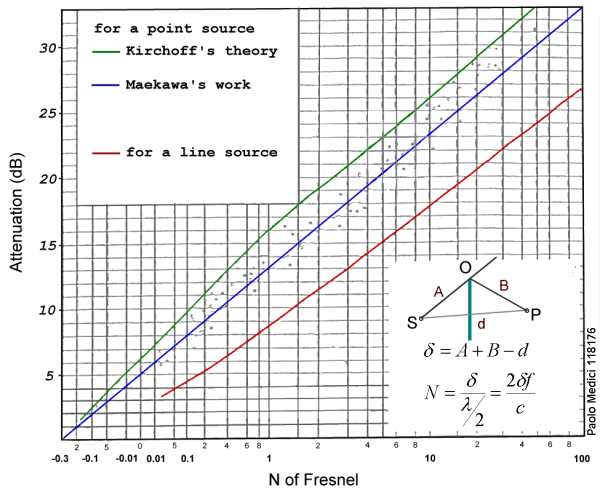
Se la sorgente è lineare invece che puntiforme l’assorbimento è inferiore di circa 5dB. Infatti, una sorgente lineare (l’autostrada) è più difficile da schermare con una barriera rispetto a una sorgente concentrata (la fabbrica).
 
 

Una formulazione alternativa è quella proposta da Kurze:

, formula che si dimostra più accurata per valori di N bassi, mentre per N elevati si ottiene la formulazione di Maekawa.