 fig.1
fig.1Università degli Studi di Parma
Corso di Laurea in Ingegneria Elettronica, Informatica, delle Telecomunicazioni
Anno accademico 1999/2000
Corso di Fisica Tecnica
Docente: Prof. Angelo Farina
Autore: Laveni Pierpaolo (plaveni@hotmail.com)
Matricola: 117327
Lezione del 5/10/99
Ore: 16:30-18:30
Argomento: Esercizi riguardanti il 1° Principio della Termodinamica
Esercizio 1
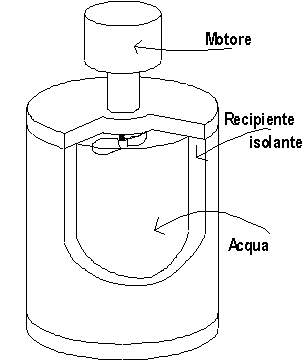
Il recipiente di fig.1 contiene 100 l di acqua. Nell’acqua c’è un’elica che dissipa energia meccanica essendo azionata da un motore. La potenza del motore è di 0.5 CV. Il motore viene azionato per un periodo
t =20 min.Calcolare la variazione dell’energia interna
D U e della temperatura D T dell’acqua sapendo che il recipiente è isolante e che il calore specifico dell’acqua è Cp = 4187 J× kg-1× K-1. fig.1
fig.1
Soluzione
Utilizzando i dati delle tabella in fondo al capitolo, riportiamo le grandezze dell’esercizio nelle unità di misura del SI.
P = 0.5 × 736 = 367.5 W
t
= 20 × 60 = 1200 sM = 100 kg
Notando che non avviene scambio di calore con l’esterno, cioè Q=0, il primo principio della termodinamica si scrive:
D
U = -LCalcoliamo, quindi, il lavoro che è negativo essendo fatto sul sistema:
L = -Pt = -368× 1200 = -441600 J
Possiamo scrivere L = -441.6 kJ in quanto non abbiamo la certezza che tutte e sei le cifre siano significative.
La variazione dell’energia è:
D
U = 441.6 kJEssendo l’acqua un liquido possiamo considerare la trasformazione sia a volume che a pressione costante, quindi il calore specifico dell’acqua a pressione costante ha lo stesso valore di quello a volume costante. Ricordando che il calore specifico è definito come la variazione dell’energia diviso la variazione della temperatura e la massa, oppure definito come la variazione dell’energia specifica diviso la variazione della temperatura:
![]()
allora la variazione della temperatura sarà:
![]()
================================================================
Nota
Nel momento in cui ci si trovi di fronte ad un problema con dei dati, bisogna accertarsi che questi siano espressi con unità del SI.
Se così non fosse dobbiamo tradurle subito in unità convenzionali. L’esercizio precedente viene risolto solo dopo aver convertito le grandezze.
Importante è anche accorgersi della differenza, per quanto che riguarda il grado d’accuratezza, tra il dato 441.6 kJ e 441600 J.
Nell’ultima espressione vediamo la presenza del dato con 6 cifre, questo perché se impostiamo il calcolo con le unità fondamentali del SI, e non dei loro multipli e sottomultipli, siamo sicuri che all’unità di misura risultante non manchino fattori di moltiplicazione.
Per finire è bene fare un controllo dimensionale sui calcoli per eliminare una gran parte degli errori di impostazione dati.
================================================================
Esercizio 2
Il recipiente di fig.2 contiene 100 l d’acqua. Nell’acqua c’è un’elica che dissipa energia meccanica. L’elica è azionata da una massa di 100 kg in caduta.
Nel recipiente vi è anche una resistenza di 0.2
W che dissipa calore per effetto Joule. La resistenza è percorsa da una corrente di 6 A per un periodo t = 5 min.Qual è l’altezza
D z da cui dovrebbe cadere il masso in modo che la variazione dell’energia interna equivalga alla variazione di energia dovuta alla resistenza?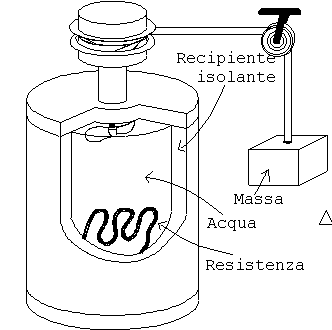 fig.2
fig.2
Soluzione
Trasformo i dati:
M = 100 kg
t
= 5× 60 = 300 sLa variazione di energia dovuta alla resistenza è data dal solo contributo del calore, cioè:
D
U = Qdove
Q = Ri2t
La variazione dovuta alla massa che cade è:
D
U = |L|dove il valore assoluto vuol indicare che, essendo entrante nel sistema, il lavoro è negativo, però contribuisce ad aumentare l’energia del sistema. Lo stesso risultato si poteva ottenere con D U = -L, ricordando che poi il segno negativo sparisce essendo il lavoro negativo.
|L| = MgD z
Uguagliando le due formule si ottiene:
Ri2t = MgD z
da qui:
![]()
NB: Siamo sicuri che il risultato è dato in metri perché abbiamo usato le grandezze fondamentali del SI.
================================================================
Esercizio 3
È data una massa di gas che compie una trasformazione passando da uno stato iniziale A ad uno stato finale B. La trasformazione è schematizzabile nel grafico di fig. 3.
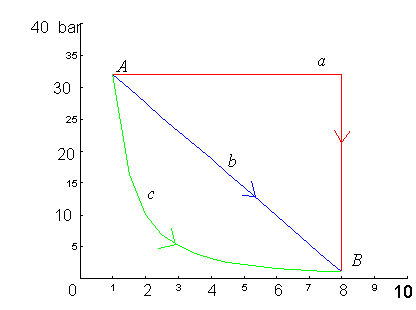 fig.3
fig.3
Sono possibili 3 differenti percorsi per avere lo stesso risultato:
pv5/3 = cost.
Confrontare le varie trasformazioni e calcolare i lavori sviluppati nei tre percorsi sapendo che pA=32 bar, pB=1 bar, vA=1 l, vB=8 l.
Soluzione
Trasformiamo le unità di misura:
pA
=32× 105 PapB=1
× 105 PavA=1
× 10-3= 0.001 m3vB=8
× 10-3= 0.008 m3Nelle prime due trasformazioni vi è scambio di calore, mentre nella terza non ve ne è, quindi l’equazione del primo principio per il percorso c si riduce a:
D
u = uA – uB = -lce sapendo che il lavoro è uguale all’area sottesa alla curva c (fig. 4), avremo:
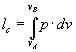
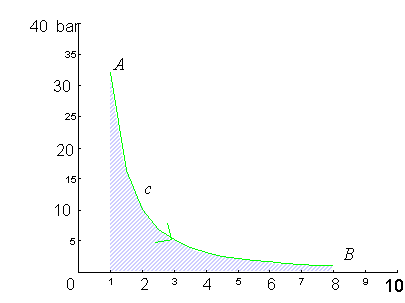 fig.4
fig.4
NB: abbiamo espresso il primo principio in grandezze intensive (energia specifica e lavoro specifico) perché non è stato specificata la massa del gas, potevamo anche usare le grandezza estensive (energia e lavoro) considerando una massa di 1 kg.
Per risolvere l’integrale precedente dobbiamo esprimere la pressione in funzione del volume specifico; utilizzando i dati iniziali si ha:
![]()
quindi
![]()
e integrando
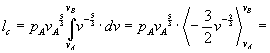
![]()
![]()
![]()
![]()
![]()
= 3600 J
Si noti che il lavoro è positivo, infatti viene fatto sull’esterno. La variazione dell’energia è D u = -3600 J.
Per il percorso a possiamo scrivere:
D
u = qa - lae il lavoro è dato dall’area sotto il grafico di fig.5
la = pA× (vB - vA) = 32× 105× (0.008-0.001) =
= 22400 J
e il calore scambiato è
qa = la + D u = 22400 – 3600 = 18800 J
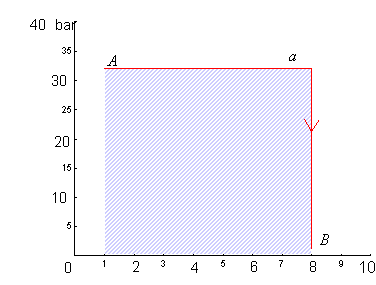 fig.5
fig.5
Per il percorso b si ha che:
D
u = qb – lbil lavoro è (fig. 6)
![]()
e il calore scambiato è
qb = lb + D u = 11550 – 3600 = 7950 J
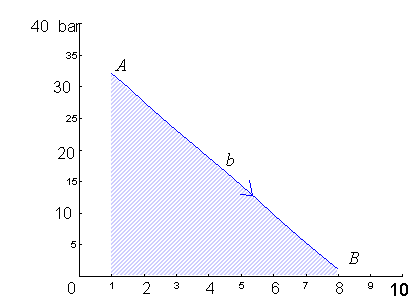 fig.6
fig.6
================================================================
Esercizio 4 – "Pompa della bicicletta" #1
Consideriamo una pompa da bicicletta schematizzata in fig.7.
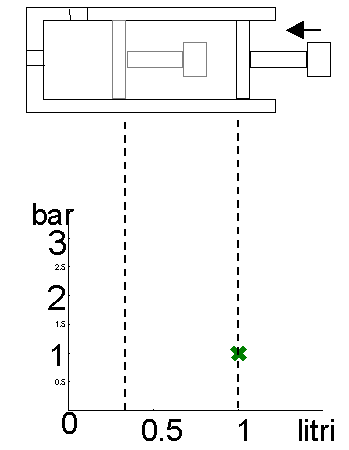 fig.7
fig.7
Spingiamo lo stantuffo molto lentamente in modo da avere una trasformazione, dello stato dell’aria, quasi statica e quindi a temperatura costante.
Sapendo che la pressione e il volume specifico iniziali sono rispettivamente p1=1 bar e v1=1 m3kg-1 e che nello stato finale l’aria ha un volume di v2=![]() v1, calcolare il lavoro svolto per comprimere l’aria e la sua pressione finale p2. Esprimere, poi, il lavoro che effettivamente noi dobbiamo svolgere per spingere lo stantuffo.
v1, calcolare il lavoro svolto per comprimere l’aria e la sua pressione finale p2. Esprimere, poi, il lavoro che effettivamente noi dobbiamo svolgere per spingere lo stantuffo.
Soluzione
Trasformiamo: p1 = 105 Pa
Dalla legge dei gas perfetti abbiamo pv = RT, ma essendo T = cost., allora pv = cost., cioè abbiamo un grafico che è un’iperbole equilatera (fig.8).
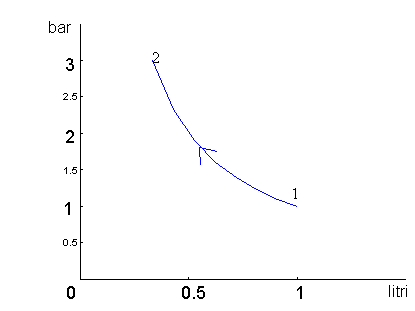 fig.8
fig.8
Possiamo quindi trovare la pressione finale che è:
![]()
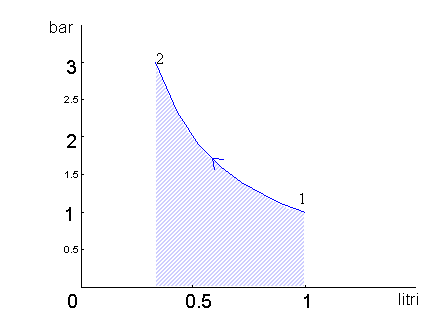 fig.9
fig.9
Il lavoro è dato dall’area sotto il grafico di fig.9
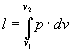
ed essendo pv = p1v1 allora p = p1v1/v, l’integrale si risolve:
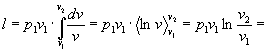
![]()
Vediamo che il lavoro è negativo in quanto svolto sul sistema.
Interessante è però accorgersi che noi non abbiamo fatto tutto il lavoro necessario per la pompata, ma solo una parte di esso. Nella fig.10 l’area segnata rappresenta il lavoro fatto dall’aria dell’atmosfera, cioè
l0 = p1× (v1-v2) = 66666 J
Il lavoro che quindi abbiamo svolto è
lnetto = 109861 – 66666 = 43195 J
positivo in quanto è stato compiuto da noi verso il sistema.
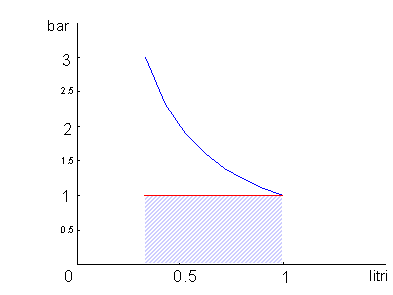 fig.10
fig.10
================================================================
Nota
Nell’esercizio precedente, arrivati a ‘![]() ’ si è passati subito alla forma ‘
’ si è passati subito alla forma ‘![]() ’ senza "passare" o comunque senza scrivere ‘
’ senza "passare" o comunque senza scrivere ‘![]() ’.
’.
Il motivo è che, analiticamente, le due forme sono uguali, ma fisicamente non ha senso il logaritmo di una grandezza fisica: essendo il logaritmo un operatore trascendente accetta solo numeri puri.
È quindi molto importante quando si fa il controllo dimensionale che gli operatori trascendenti abbiano come argomento numeri puri, altrimenti la formula non è corretta. Ad esempio, nel caso precedente ‘v1/v2‘è un numero puro, mentre v1 e v2 non lo sono.
================================================================
Esercizio 5 – "Pompa della bicicletta" #2
Riprendendo l’esercizio precedente si ha che, continuando nella pompata, la valvola di sfiato della pompa si apre, l’aria viene convogliata nella camera d’aria e poi, arrivati a "fondo corsa", si inverte il senso della pompata ricaricando la pompa nuovamente d’aria.(fig.11)
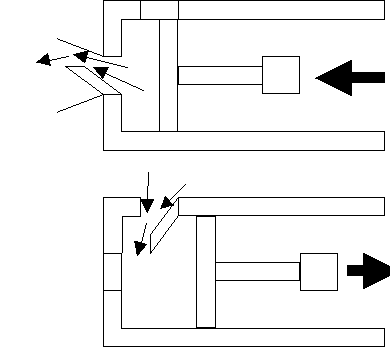 fig.11
fig.11
Descrivere cosa avviene nel sistema.
Soluzione
Quando l’aria compressa esce dalla pompa, il volume continua a diminuire fino a zero, mentre la pressione dell’aria si mantiene costante. (fig.12)
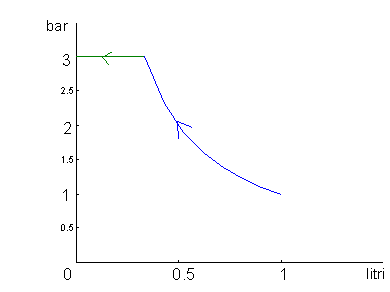 fig.12
fig.12
Nel momento di ricaricare la pompa, l’aria che entra ha la pressione atmosferica, quindi la pressione dell’aria rimane costante mentre aumenta il volume. (fig.13)
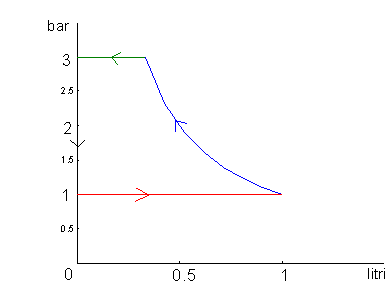 fig.13
fig.13
Notiamo che ora non siamo più di fronte ad un sistema chiuso, ma ad uno aperto.
Il lavoro del sistema aperto si calcola come:
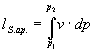
cioè il lavoro complessivo che viene fatto sul sistema è uguale all’area racchiusa nel cammino complessivo. (fig.14)
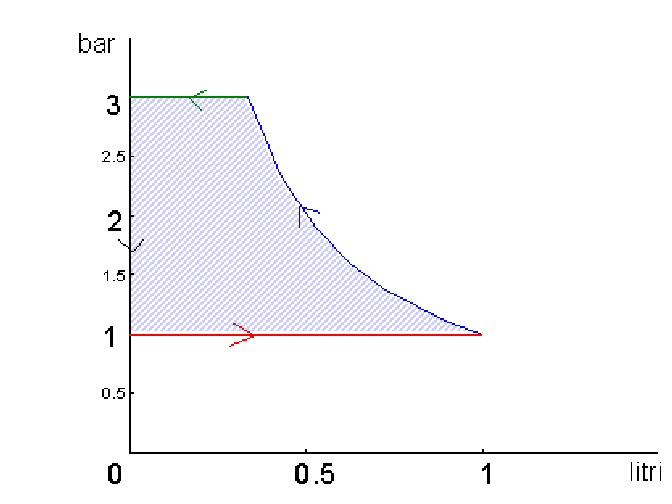 fig.14
fig.14
================================================================
Esercizio 5
Risolvere intuitivamente questo problema.
Una pompa preleva dell’acqua da una vasca. (fig.15) Alla sommità della pompa si registra, con un barometro, una pressione di 3 bar.
 fig.15
fig.15
Calcolare la prevalenza della pompa, cioè l’altezza teorica H a cui la pompa potrebbe sollevare l’acqua.
Soluzione
Sapendo che una colonna d’acqua di circa 10 m ha una pressione alla base di 1 bar, la pompa riesce a sopportare 3 volte questa pressione, quindi la prevalenza sarà di 30 m.
================================================================
Esercizio 6
Risolvere intuitivamente questo problema.
Un uomo si trova 20 m sott’acqua (fig.16) e riceve aria da un respiratore che eroga l’ossigeno alla stessa presione dell’acqua in cui si trova. Presa una boccata d’aria l’uomo si dà un colpo di pinne e risale.
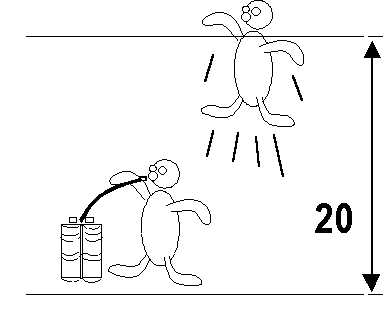 fig.16
fig.16
Supponiamo che l’uomo abbia nei polmoni 5 litri d’ossigeno: cosa accade quando egli giunge in superficie? Galleggia? Che spinta idrostatica ha nelle vicinanze della superficie?
Soluzione
L’aria erogata dal respiratore ha una pressione di 3 bar. (2 bar dati dai 20 m d’acqua, e 1 bar doto dall’atmosfera)
L’aria contenuta nei polmoni può essere vista come un sistema termodinamico chiuso a temperatura costante (37°C), quindi possiamo dire che pv = cost.
Arrivato alla superficie, la pressione dell’aria nei polmoni è di 1 bar, quindi il volume sale a
![]()
L’uomo, se è ancora vivo, galleggia in quanto conserva il suo peso (il peso di 15 litri di aria è irrilevante), ma il suo volume aumenta di 10 l.
La spinta idrostatica sarà circa pari al peso dell’uomo più 10 kg, dati dal volume d’acqua, in più, nei polmoni..
================================================================
Esercizio 7
Risolvere intuitivamente questo problema.
Una pentola contenente 10 libbre di acqua è scaldata in modo tale da far aumentare la sua temperatura da 0°R a 80°R, e da 32°F a 212°F.
Qual è il calore scambiato nei due casi?
Soluzione
Convertendo le grandezze in unità più conosciute abbiamo che la variazione della temperatura in entrambi i casi è da 0°C a 100°C e che 10 libbre (GB) equivalgono a 4356 g.
Per elevare di 100 gradi un grammo d’acqua servono 100 calorie, quindi il calore scambiato è:
Q = 435600 cal = 1822.55 kJ
================================================================
Fattori di conversione fra differenti unità di misura
|
Potenza |
W |
Kpm/s |
CV |
HP |
|
W |
1 |
0.102 |
1.36 × 10-3 |
1.34 × 10-3 |
|
Kpm/s |
9.80 |
1 |
0.01333 |
0.01315 |
|
CV |
736 |
75 |
1 |
0.986 |
|
HP |
745.2 |
76.04 |
1.014 |
1 |
Legenda:
Kpm/s : kilogrammetro al secondo
W : watt
CV : cavallo-vapore
HP : horse-power
|
Energia |
J |
erg |
cal |
eV |
|
J |
1 |
10-7 |
0.239 |
6.24× 1018 |
|
erg |
107 |
1 |
4.184× 10-7 |
6.24× 1011 |
|
cal |
4.184 |
4.184× 107 |
1 |
2.61× 1018 |
|
eV |
1.602× 10-19 |
1.602× 10-12 |
3.83× 10-20 |
1 |
Legenda:
J : Joule
erg : Erg
cal : Caloria
eV : elettronvolt
|
Pressione |
Pa |
atm |
bar |
torr (mmHg) |
mH2O |
kp/cm2 |
|
Pa |
1 |
9.869× 10-6 |
10-5 |
7.5× 10-3 |
1.019× 10-4 |
1.019× 10-5 |
|
atm |
1.013× 105 |
1 |
1.013 |
760 |
10.33 |
1.033 |
|
bar |
105 |
0.9869 |
1 |
750 |
10.2 |
1.02 |
|
torr (mmHg) |
1.333× 102 |
1.31× 10-3 |
1.333× 10-3 |
1 |
0.0135 |
0.00135 |
|
mH2O |
9.81× 103 |
0.0968 |
0.098 |
74 |
1 |
0.1 |
|
kp/cm2 |
9.81× 104 |
0.968 |
0.98 |
740 |
10 |
1 |
Legenda:
Pa : Pascal (N/m2)
atm : atmosfera
torr : torricelli o millimetri di mercurio
mH2O : metri d’acqua
kp/cm2 : chilogrammosucentimetroquadrato
Relazioni fra scale di temperatura
T(K) = T(°C) + 273.15 = 5/9 T(°F) + 255.37 = 5/4 T(°R) +273.15
T(°C) = T(K) – 273.15 = 5/9 [T(°F) – 32] = 5/4 T(°R)
T(°F) = 9/5 [T(K) – 255.37] = 9/5 T(°C) +32 = 9/4 T(°R) +32
T(°R) = 4/5 [T(K) – 273.15] = 4/5 T(°C) = 4/9 [T(°F) –32]
|
Relazioni intuitive |
Congelamento dell’acqua |
Ebollizione dell’acqua |
|
K |
273.15 |
373.15 |
|
°C |
0 |
100 |
|
°F |
32 |
212 |
|
°R |
0 |
80 |
Legenda:
K : Kelvin o scala di Temperatura Assoluta o Termodinamica
°C : Grado Celsius o Centigrado
°F : Grado Fahrenheit (grado britannico e statunitense)
°R : Grado Réamur o Ottantigrada (grado tedesco)
Relazione tra scale di peso
1 lb(USA) = 453.60× 10-3 kg
1 lb(GB) = 435.60× 10-3 kg