
Fig. 1 - Esempio di fonometro
MISURE FONOMETRICHE
Il fonometro è uno strumento per misurare l'intensità dei suoni. I fonometri più famosi sono danesi (in particolare Bruel & Kjaer), ma in questa lezione faremo uso di uno fonometro italiano, quello della Delta Ohm.

Fig. 1 - Esempio di fonometro
Le componenti funzionali di un fonometro possono essere rappresentate da un diagramma a blocchi.
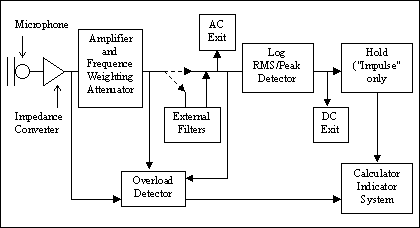
Fig. 2 - Digramma dei blocchi funzionali
Il punto di ingresso del segnale è il rappresentato dal microfono (la parte più importante e costosa del fonometro) in cui si realizza la conversione tra pressione sonora e segnale elettrico. La caratteristica fondamentale di un microfono è la sua sensibilità, espressa dal rapporto tra la tensione prodotta in mV e la pressione sonora applicata, in Pa, con un range di valori che va da 2 a100 mV/Pa. Il nostro strumento ha una sensibilità di 50 mV/Pa.
Teoricamente un microfono dovrebbe essere omnidirezionale. In pratica però non lo è mai perfettamente, almeno non alle alte frequenze. Per questo motivo sono state realizzate due diverse tipologie: a campo libero o a campo diffuso. Quello che utilizziamo in questa lezione è a campo libero.
Un microfono a campo libero si usa puntandolo nella direzione da cui proviene il suono, come in Fig. 3.
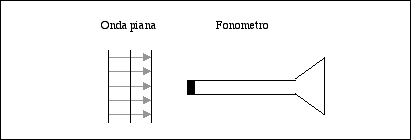
Fig. 3 - Schema del microfono a campo libero
Utilizzato correttamente dà risposta in frequenza piatta. Tuttavia, se viene usato in modo errato (ad esempio ponendolo a 90° rispetto alla fonte che produce il suono che voglio misurare) sottostima le componenti ad alta frequenza, perché perde parte del segnale.
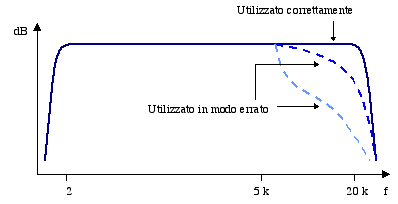
Fig. 4 - Risposta in frequenza per un microfono a campo libero
Quindi, se si devono effettuare delle misurazioni in un campo sonoro diffuso, senza una direzione privilegiata da cui provenga il suono, si utilizza un microfono a campo diffuso, che va posto a circa 90° rispetto alla fonte da cui proviene il suono.
Come per il microfono a campo libero, se l'utilizzo non è corretto il grafico della risposta in frequenza non sarà piatto, ma avrà delle variazioni sulle alte frequenze (in questo caso verranno eccessivamente amplificate).
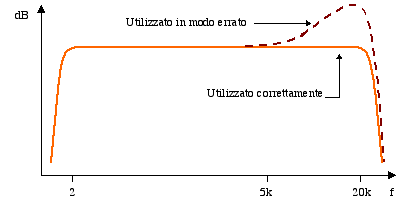
Fig. 5 - Risposta in frequenza per il microfono a campo diffuso
Ad ogni misurazione dovremmo teoricamente fare uso due diversi microfoni, secondo le diverse condizioni. È necessario ricordare però che il microfono è la parte più costosa di un fonometro. Nella pratica quindi se ne acquista soltanto uno e poi, effettuata la misurazione, si riequilibrano le alte frequenze che sono state sovrastimate o sottostimate.
Esistono anche delle maschere di tolleranza che permettono di accertarsi di effettuare misure a norma di legge. Per esempio in Italia le misurazioni fonometriche devono essere effettuate con microfoni di Classe 1 (ovvero microfoni di precisione), caratterizzati da una ristretta maschera di tolleranza e dal funzionamento a pressione, il che evita "effetti di prossimità" (significa che danno lo stesso risultato anche se posti molto vicini alla fonte che produce il suono, senza amplificare eccessivamente le basse frequenze ).
Subito dopo il blocco funzionale del microfono (chiamato anche capsula microfonica, perché può essere avvitato all'estremo del fonometro) troviamo il convertitore di impedenza. La necessità di questo dispositivo dipende dal fatto che il microfono interno ad un fonometro è un condensatore, costituito da una sottile membrana e da un piattello rigido (Fig. 6).
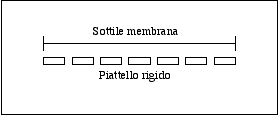
Fig. 6 - Schema del microfono a condensatore
Dato che il microfono non ha propria carica, è necessario applicare ai capi del condensatore una tensione di polarizzazione fissata a 200 V. Quando la pressione generata da un'onda sonora arriva alla membrana, la distanza tra le due armature diminuisce, andando a variare la capacità del condensatore stesso. In questo modo varia anche la tensione e il segnale elettrico che esce è la differenza di potenziale rispetto alla tensione di polarizzazione introdotta. A questo punto per considerare solo le variazioni di tensione si inserisce un condensatore in serie che reietta la componente continua.
Si capisce così che il microfono non andrà a misurare pressioni statiche, ma solo variazioni rispetto alla pressione atmosferica, a partire dalla frequenza di taglio del condensatore applicato (che di solito è limitata a 2 o 3 Hz).
Tuttavia la sovratensione che devo misurare esiste solo a circuito aperto, perché se attaccassi un campo resistivo, il condensatore si scaricherebbe subito: dovrei allora applicare ai capi del condensatore una resistenza infinita (il che è impossibile in pratica da ottenere). Per realizzare quest'effetto si utilizza appunto un convertitore di impedenza realizzato con un transistor ad effetto di campo, con guadagno unitario (e quindi nessun effetto amplificativo).
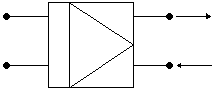
Fig. 7 - Schema del transistor ad effetto di campo
Come si vede in Fig. 7, a destra del transistor possono circolare le correnti, mentre sulla sinistra questo non avviene (come se il circuito fosse aperto).
Il blocco funzionale che segue è molto importante perché contiene un attenuatore di guadagno e i filtri di ponderazione.
L'attenuatore di guadagno consente di variare il fondo della scala di misurazione dello strumento. I migliori fonometri raggiungono un campo di misura di 110 dB: per tali strumenti allora non è strettamente necessario un dispositivo di questo tipo. Tuttavia la maggior parte dei fonometri effettivamente in uso non hanno range di sensibilità così alti (perché il minimo per essere dichiarati di Classe 1 è di 60 dB) e quindi poter variare il fondo della scala risulta molto utile. Il nostro fonometro ad esempio ha quattro possibili tarature:
In questo blocco sono contenuti anche i filtri di ponderazione A, B, C e D (non sempre sono tutti e quattro presenti, dipende dalle caratteristiche del fonometro stesso).
Nel diagramma compare poi un blocco esterno contenente i filtri per l'analisi in frequenza. Non tutti i fonometri però hanno un'uscita per i filtri, perché spesso (soprattutto quelli più moderni) li hanno già interni. Quello che usiamo noi, ad esempio, li ha nello stesso blocco dei filtri per la ponderazione, cosa che ci evita gravi errori: infatti in questo modo se applico la ponderazione A non posso contemporaneamente eseguire l'analisi in frequenza. Molto spesso invece con i filtri esterni questa regola viene trascurata: si applica la ponderazione e poi si realizza l'analisi in frequenza (dimenticandosi che così facendo le varie frequenze risultano, apparentemente senza motivo, più basse del previsto).
Un altro blocco molto importante è l'indicatore di sovraccarico. Infatti se ci dovessimo sbagliare nel settare il fondo della scala, un suono troppo forte (o troppo debole) potrebbe eccedere il valore massimo (o minimo) visualizzato, così da farci leggere una misura errata. Con questo dispositivo invece posso controllare direttamente sul display che la misura effettuata sia effettivamente interna al range inizialmente selezionato.
Dopo i filtri esterni troviamo la conversione da forma d'onda a valore RMS: la forma d'onda stessa viene raddrizzata, elevata al quadrato e convertita da lineare a logaritmica, tramite circuiti integrati specifici. All'interno di questo blocco si trovano le costanti di tempo del circuito RC.
Il blocco successivo permette di trattenere il valore massimo del segnale che lo attraversa.
Seguendo l'andamento del segnale si arriva quindi nella parte digitale dello strumento che ha unicamente la funzione di display.
Un fonometro può avere anche due (o più) uscite elettriche: AC da cui esce il segnale in modo da poter essere registrato, e DC (ormai non più utilizzata) in tensione continua.
Il nostro strumento ha due uscite AC: una pre-filter e l'altra post-filter. Queste rappresentano una grande comodità. Infatti tenendo il fonometro in ponderazione A, sulla prima uscita si avrà il segnale non ponderato, ottimo per l'analisi in frequenza, e sulla seconda si avrà il segnale con la ponderazione A, ottimo invece per valutare ad esempio il livello complessivo.
Si deve ora ricordare che un fonometro in realtà non misura il livello equivalente, né il valore medio lineare: misura solo i valori istantanei con costanti di tempo FAST, SLOW o IMPULSE.
La legge italiana tuttavia, con il decreto misure del marzo '98 (clicca qui per scaricarlo!) impone il calcolo del livello equivalente, dato dalla formula
(1)
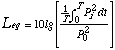
dove Pi indica la pressione istantanea ponderata A e il numeratore dell'argomento del logaritmo é il valore medio efficace della pressione (fatto senza costante di tempo) che tiene conto di tutti gli istanti della misurazione.
Ma allora come è possibile conciliare la caratteristica dello strumento di effettuare le misurazioni con costanti di tempo, con i termini di legge?
Consideriamo a proposito un segnale generico, misurato per un tempo T. Poiché la costante di tempo FAST di un circuito RC è
RC = 125 ms
è necessario che lo strumento per costruire correttamente il diagramma nel tempo, campioni in valore FAST almeno 8 volte al secondo. In questo modo si ha la garanzia che il segnale mantenga la sua continuità nel dominio del tempo: con una misura ad esempio di 10 minuti lo strumento deve leggere
(600 s)x(8 numeri / s) = 4800 numeri.
Quindi la parte finale (digitale) dello strumento campiona il segnale in componente continua dopo il convertitore lineare-logaritmico e questo segnale viene ricostruito con il campione ogni 125 ms. Da questo si calcola poi il livello equivalente.
I dati con cui lavoriamo, però, sono valori di livello e non di pressione: allora la formula effettivamente utilizzata è la seguente, in cui compare come argomento del logaritmo il valor medio energetico
(2)
![]()
In questa formula si riassume il funzionamento del fonometro, che prima campiona con costante FAST il segnale in entrata e poi calcola il Leq con il valor medio di tutti i dati campionati.
Il valore di Leq viene aggiornato nel corso della misura e in particolare, con un segnale stazionario, tende a stabilizzarsi (come in Fig. 8 in cui compare il rumore provocato da un ventilatore che si accende e si spegne).
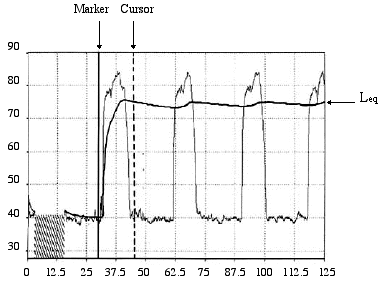
Fig. 8 - Valutazione di Leq per un segnale stazionario
Vediamo ora un esempio numerico che chiarisca il calcolo di Leq. Consideriamo il seguente grafico realizzato con costante di tempo FAST.
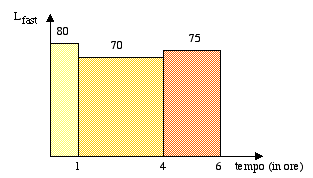
Fig. 9 - Diagramma dei livelli
Voglio determinare il valore complessivo di Leq.
In questo caso non ha importanza l'ordine in cui calcoliamo i contributi di ogni livello, perché all'interno del logaritmo verrà fatta comunque la somma di tutti i termini.
Come prima cosa convertiamo le ore in minuti.
6 ore = 360 minuti
da cui N = 360. Allora applicando la (2)
![]()
Ci si può ora chiedere per quale motivo abbiamo convertito le ore ai minuti. In realtà questa trasformazione è stata puramente formale, perché il calcolo comunque non cambia (perché dipende da un rapporto!). Infatti con le ore lo stesso calcolo diventa
![]()
Oltre al livello equivalente Leq va considerato per legge anche il livello di esposizione personale (giornaliero) Lep che va dichiarato per ogni lavoratore soggetto alla tutela da rischi fisici in ambienti di lavoro. Diversamente da Leq che è calcolato sul tempo effettivo di esposizione, il valore di Lep è calcolato sempre su 8 ore lavorative.
Per capirci torniamo all'esempio precedente. Mentre prima avevamo N = 6, ora prendiamo N = 8 e il calcolo diventa
![]()
Un ulteriore esempio può essere quello degli studenti universitari che pur avendo 8 ore di lezione in un'aula (a 75 dB(A) ), alla fine della giornata hanno passato in aula circa 10 ore (perché arrivano prima, stanno in aula a studiare o vi trascorrono la pausa pranzo). In questo caso il livello di esposizione personale Lep è
![]()
dove 10 sono le ore effettive di esposizione.
Da quello che abbiamo detto su Lep e Leq si capisce che non è dannoso il livello sonoro in sé (a patto di stare sotto una certa soglia), ma piuttosto l'esposizione prolungata ad esso.
Per la misura di Leq è necessario effettuare il campionamento della storia temporale. Questo stesso campionamento ha un'ulteriore rilevanza, dovuta al decreto misure del marzo '98 che afferma che sul suono misurato posso essere effettuate tre possibili correzioni:
Per ogni correzione di questo tipo vengono addizionati 3 dB e il livello del rumore ambientale L è dato dalla somma
(3)
L = Leq + C1 + C2 + C3
E' necessario allora determinare secondo il decreto misure del marzo '98 che cosa si intenda per rumore impulsivo. Il decreto afferma che:
"Il rumore è considerato avente componenti impulsive quando sono verificate le condizioni seguenti:
La prima condizione è chiarita nel decreto qualche riga più avanti.
"L’evento sonoro impulsivo si considera ripetitivo quando si verifica almeno 10 volte nell’arco di un’ora nel periodo diurno ed almeno 2 volte nell’arco di un’ora nel periodo notturno."
Passiamo quindi al secondo punto. LAImax e LASmax rappresentano rispettivamente il massimo livello misurato secondo la metodologia IMPULSE e secondo la metodologia SLOW. Allora per avere un rumore impulsivo deve valere la condizione
(4)
LAImax - LASmax > 6 dB
La (4) tuttavia è verificata anche dalla voce umana (il che significa che è una condizione debole, perché facilmente verificabile). Per questo motivo è stata introdotta la terza condizione, dove compare il termine LAFmax che indica il massimo livello misurato con la costante di tempo FAST. La terza condizione può essere schematizzata dal seguente grafico.
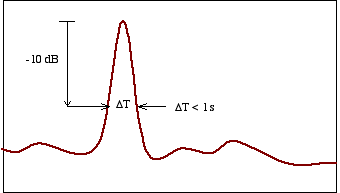
Fig. 10 - Verifica della componente impulsiva
Data la traccia FAST del segnale, deve essere verificato che, abbassandosi di 10 dB rispetto al valore massimo, la durata dell'impulso sia minore di un secondo. Si vede così che è necessario misurare contemporaneamente la storia temporale con le tre costanti di tempo IMPULSE, FAST e SLOW. Tuttavia l'unico strumento che permette direttamente una misura di questo tipo è il fonometro della Larson Davis ed è molto costoso. La maggior parte dei fonometri invece permette una misurazione per volta. Quindi l'unica soluzione è quella di registrare il segnale e poi inserirlo nuovamente nel fonometro in metodologia IMPULSE, FAST e SLOW.
Devo però fare attenzione a registrare il segnale in modo da non perdere nessuna informazione e da non introdurre nessun disturbo. Un modo corretto è quello di registrarlo su disco fisso nel computer o su un sistema di registrazione "senza perdite". Infatti se decidessi di fare la registrazione ad esempio su un CD, perderemmo molte delle informazioni necessarie, proprio perché il CD utilizza algoritmi di compressione che perdono parte del segnale.
Sempre utilizzando il decreto, determiniamo ora come riconoscere le componenti tonali di un rumore.
"Al fine di individuare la presenza di componenti tonali nel rumore, si effettua un’analisi spettrale per bande normalizzate di 1/3 di ottava. L’analisi deve essere svolta nell’intervallo di frequenza compreso tra 20 Hz e 20 kHz. Si considerano esclusivamente le componenti tonali aventi carattere stazionario nel tempo ed in frequenza. Se si utilizzano filtri sequenziali si determina il minimo di ciascuna banda con costante di tempo Fast. Se si utilizzano filtri paralleli, il livello dello spettro stazionario è evidenziato dal livello minimo in ciascuna banda."
Il decreto richiede di fare un’analisi spettrale per bande normalizzate di 1/3 di ottava, considerando solo le componenti di carattere stazionario (in tempo e in frequenza). Si deve poi determinare il minimo di ogni banda con costante di tempo FAST e realizzare il diagramma frequenza per frequenza delle bande così normalizzate.
Il decreto quindi continua:
"Si è in presenza di una componenti tonale se il livello minimo di una banda supera i livelli minimi delle bande adiacenti per almeno 5 dB"
Può tuttavia sorgere un problema: dato che i filtri di 1/3 di ottava hanno i fianchi non verticali (Fig. 11), può avvenire una sovrapposizione di due bande, il che nasconde la presenza della componenti tonali stesse, perché fa elevare allo stesso modo due bande vicine.
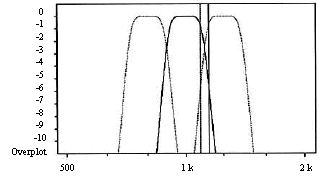
Fig. 11 - Grafico del filtro di 1/3 di ottava
Il decreto a proposito afferma che:
"Per evidenziare componenti tonali che si trovano alla frequenza di incrocio di due filtri ad 1/3 di ottava, possono essere usati filtri con maggiore potere selettivo o frequenze di incrocio alternative."
Quindi si deve effettuare un'ulteriore misurazione in 1/6 di ottava e poi riunire nei due differenti modi possibili (Fig. 12 a) e b) ) i 1/6 di ottava per formare due grafici in 1/3 di ottava: confrontando questi due, si potrà determinare la presenza o meno delle componenti tonali.
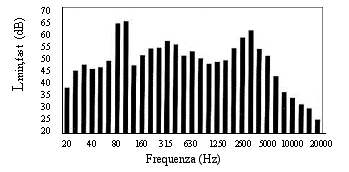
Fig. 12 a) - Spettro in terzi di ottava (primo modo)
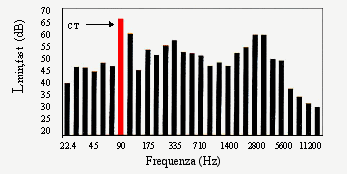
Fig. 12 b) - Spettro in terzi di ottava (secondo modo)
In questo caso si vede che la componente a 90 Hz potrebbe essere una componente tonale perché supera i livelli minimi delle bande adiacenti per almeno 5 dB.
Con un semplice calcolo si può inoltre determinare la probabilità di avere sovrapposizione. Infatti confrontando in Fig. 11 la larghezza della zona di incrocio che misura 54 Hz con la larghezza del filtro di ottava (di 174 Hz) scopriamo che (considerando sia il fianco destro che quello sinistro) la probabilità di avere una sovrapposizione è circa del 31% (quindi molta alta!).
Prima di applicare il fattore di correzione di 3 dB(A), deve essere fatto un ultimo controllo:
"Si applica il fattore di correzione soltanto se la componenti tonali .tocca una isofonica eguale o superiore a quella più elevata raggiunta dalle altre componenti dello spettro."
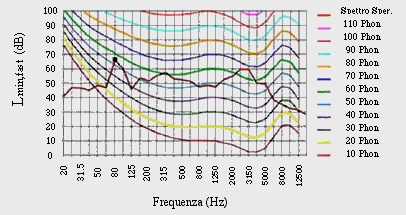
Fig. 13 - Verifica della componente tonale con le isofoniche
Ad una prima osservazione del grafico sembrerebbe che la componente tonale a 80 Hz svetti sulle altre, cioè sia quella che raggiunge l'altezza maggiore. Prendiamo però in considerazione l'isofonica verde al centro del digramma di Fletcher e Manson. Riferendoci a questa curva, si vede che altre due vette, più elevate di quella a 80 Hz, la intersecano e la superano. Questo allora significa che la componente tonale a 80 Hz non è da penalizzare con il fattore correttivo, perché non "svetta" sul diagramma delle isofoniche stesso.
Determiniamo infine come si verifica la presenza di una componente tonale a bassa frequenza.
"Se l’analisi in frequenza svolta con le modalità precedentemente esposte, rivela la presenza di componenti tonali tali da consentire l’applicazione del fattore correttivo C2 nell’intervallo di frequenze compreso fra 20 Hz e 200 Hz, si applica anche la correzione C3, esclusivamente nel tempo di riferimento notturno."
Quindi siamo in presenza di una componente tonale a bassa frequenza se sono verificate le tre seguenti condizioni:
In questo caso allora, oltre alla correzione per la componente tonale generale, viene applicata anche quella per la componente tonale a bassa frequenza (anch'essa di 3 dB(A) ).
ANALISI STATISTICA
Torniamo ora al grafico che rappresenta il livello equivalente Leq di un ventilatore che si accende e si spegne (Fig. 8). In questo caso i livelli sono molto separati, per cui è semplice distinguere le fasi in cui il ventilatore è spento e quelle in cui è in funzione. Tuttavia non sempre la situazione é così chiara. Nell'esempio di Fig. 14 il livello sonoro misurato nell'arco di un giorno nei pressi di una strada trafficata e di una ferrovia varia in maniera apparentemente caotica (ogni singolo dato campionato è un livello equivalente di un minuto).
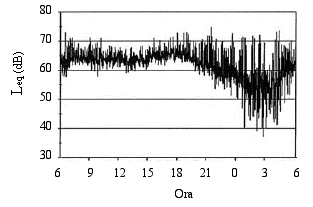
Fig. 14 - Livello sonoro equivalente
Come si può, con una misura di questo tipo, separare i contributi delle diverse sorgenti sonore?
E' necessario fare l'analisi statistica dell'evento, che risponde alla domanda: qual è la percentuale di tempo in cui c'è stato un certo livello (in un certo range)? Applicando questo concetto al caso più semplice del ventilatore si ottiene una distribuzione statistica bimodale come in Fig.15.
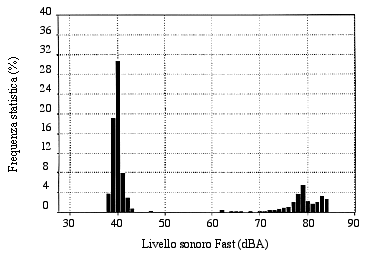
Fig. 15 - Distribuzione statistica (bimodale)
In questo esempio si ottiene una distribuzione in cui i due contributi sono molto separati, quindi diventa tecnicamente possibile calcolare la distribuzione dei livelli equivalenti parziali, data dalla formula
(5)
![]()
In questo modo posso calcolare il livello equivalente parziale del ventilatore in funzione, senza l'effetto del rumore di fondo.
Prendiamo ora come esempio il rumore provocato da un aereo in volo. Consideriamo l'evento sonoro dovuto all'aereo stesso (Fig. 16 a) ) e la sua analisi statistica distributiva (Fig. 16 b) ).
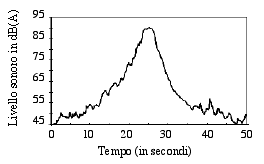
Fig. 16 a) - Evento sonoro
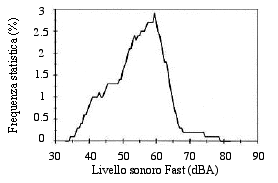
Fig. 16 b) - Analisi statistica
Anche in questo caso però l'analisi è semplice perché c'è una sola sorgente.
Un caso un po' più complicato é quello dell'analisi statistica del diagramma di Fig.14 la cui distribuzione ha due picchi che si sovrappongono per un certo intervallo (Fig. 17).
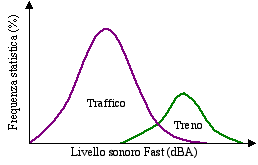
Fig. 17 - Analisi statistica
Esiste un'ulteriore analisi statistica (di secondo livello o cumulativa), che consiste nel porsi la domanda: per quanto tempo si è superato un certo livello?
L'analisi statistica cumulativa si ottiene facendo l'integrale della curva della distribuzione statistica. Riferendoci all'evento della Fig.16 a), otteniamo il digramma che rappresenta questa seconda analisi integrando la curva di Fig. 16 b).
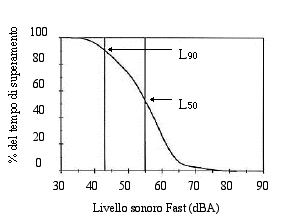
Fig. 18 - Analisi statistica cumulativa
Su questa curva si delinea un nuovo tipo di livelli sonori: i livelli percentivi. Questi sono definiti come i livelli che vengono superati per una frazione assegnata del tempo. Nella Fig. 18 si vedono ad esempio segnati L90 e L50: L90 è quel livello che viene superato per il 90 % del tempo, mentre L50 è la mediana della distribuzione statistica, cioè quel dato per cui si ha uguale probabilità di avere un valore superiore o inferiore. I valori percettivi classici sono
| L1 | L5 | L10 | L50 | L90 | L95 | L99 |
Normalmente un analizzatore statistico per disegnare il grafico non memorizza tutti i valori dei livelli, ma convenzionalmente se ne scelgono 7 di riferimento (di cui 5 tra quelli classici). Effettivamente c'è una perdita di contenti, ma con 7 numeri la curva si riesce ancora a ricostruire (cosa che sarebbe invece impossibile per la curva distributiva, soprattutto nel caso bimodale).
Torniamo ad analizzare come esempio il caso del ventilatore. Dalla curva statistica distributiva di Fig. 15 si ricava la distribuzione cumulativa di Fig. 19.
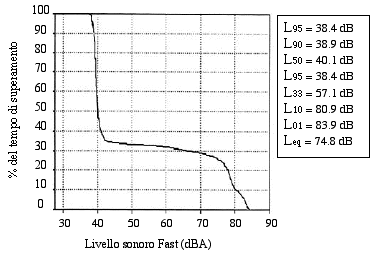
Fig. 19 - Distribuzione statistica cumulativa
dove c'è una grossa caduta di percentuale di tempo attorno ai 40 dB e poi un ulteriore caduta verso i livelli molto alti del ventilatore. Il livello massimo è 86 dB e quello minimo è 38 dB. In mezzo ci sono i livelli percentivi. Ad esempio L50 è 40.1 dB, mentre L95 è circa 38.4 dB.
Un'ultima nota importante: l'analisi statistica va sempre fatta a partire da dati FAST, altrimenti la curva distributiva viene alta e stretta, e si perde il valore statistico stesso della misura!